
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции в точке
|
|
|
|
Определение 1. (по Гейне)
Постоянное число А называется пределом функции f(x) в точке  (или при
(или при 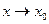 ) если для
) если для 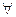 последовательности
последовательности 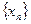 такой, что
такой, что 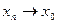 и
и 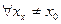 соответствующая последовательность значений функций
соответствующая последовательность значений функций 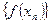 сходится А.
сходится А.
Пишем: 
Определение 2. (по Коши)
Постоянное число А называется пределом функции  в точке
в точке  (или при
(или при 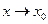 ) если для произвольного числа
) если для произвольного числа 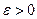 найдется число
найдется число  такое, что из условия
такое, что из условия 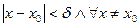 (1) вытекает неравенство
(1) вытекает неравенство  .
.
Определение 2. (в кванторах)

Комментарий к определению по Коши.
Означает, что значение функции  будут как угодно мало отличаться от постоянного числа А, если только соответствующее значение аргумента близки к
будут как угодно мало отличаться от постоянного числа А, если только соответствующее значение аргумента близки к  .
.
Доказывается что определения 1 и 2 эквивалентны.
Геометрическая интерпретация определения по Коши. Т.к. неравенство (1) равносильно:  то какова бы ни была полоса, ограниченная прямыми
то какова бы ни была полоса, ограниченная прямыми  и
и 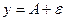 , найдется интервал
, найдется интервал 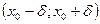 , такой что все точки графика
, такой что все точки графика 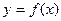 с абсциссами из этого интервала (кроме быть может точки с абсциссами
с абсциссами из этого интервала (кроме быть может точки с абсциссами  ) окажутся внутри данной полосы.
) окажутся внутри данной полосы.
 | |||
 | |||



 A
A


 |


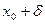
Подчеркнем, что определение Коши не требует, что бы функция  была определена в точке
была определена в точке  , поэтому в определении речь идет о проколотой
, поэтому в определении речь идет о проколотой 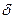 - окрестности точки
- окрестности точки  -
- 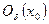 (окрестность точки
(окрестность точки  радиуса
радиуса 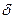 ).
).
 . (
. (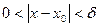 - показывает что
- показывает что  ).
).
Примеры:
I.  ,
, 
рассмотрим две последовательности  ясно, что первая последовательность стремится к 0 при
ясно, что первая последовательность стремится к 0 при 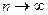 и вторая так же стремиться к 0 при
и вторая так же стремиться к 0 при 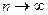 .
.
Но:  ;
;
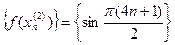
Очевидно,  ,
, 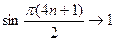 .
.
Видим, что соответствующие последовательности значений функций имеют разные пределы 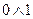 . Таким образом определение Гейне не удовлетворяет. Следовательно функция
. Таким образом определение Гейне не удовлетворяет. Следовательно функция 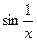 в точке
в точке  предела не имеет.
предела не имеет.
II. 
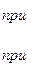

При  имеем:
имеем:
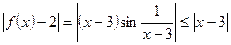
Выбираем произвольно 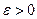 и положим
и положим  , тогда
, тогда  влечет или в символах:
влечет или в символах:  , т.е.
, т.е. 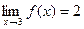 .
.
Видим, что предел функции в точке x=3 существует, а значение функции в этой точке тут совершенно ни при чем. Мы могли бы придать функции значение или не придавать никакое.
Непрерывность функции в точке.
Определение 2.
Функция  называется непрерывной в точке
называется непрерывной в точке  если:
если: 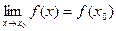 (2).
(2).
Это определение предъявляет функции  следующие требования:
следующие требования:
1) функция  должна быть определена в точке
должна быть определена в точке  и некоторой ее окрестности.
и некоторой ее окрестности.
2) Функция  должна иметь в точке
должна иметь в точке  предел.
предел.
3) Этот предел должен совпадать со значением функции в точке  .
.
Определение 2 означает, что для непрерывности в точке  функции знаки lim и f функции перестановочны, т.е.
функции знаки lim и f функции перестановочны, т.е. 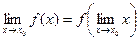 . Предел функции равен функции от предела аргумента.
. Предел функции равен функции от предела аргумента.
Если хотя бы одно из трех требований предъявляемым к функции  в определении 2 не выполняется, то говорят, что функция
в определении 2 не выполняется, то говорят, что функция  разрывна в т.
разрывна в т.  или имеет в т.
или имеет в т.  разрыв; при этом предполагается, что функция
разрыв; при этом предполагается, что функция  определена в некоторой окрестности
определена в некоторой окрестности  кроме быть может т.
кроме быть может т. .
.
Тогда т.  - называется точкой разрыва функции
- называется точкой разрыва функции  .
.
Определение 2 аналитически выражает интуитивное представление о непрерывности графика функции т.е. кривой  .
.
Например такую кривую можно провести отрывая карандаша от бумаги.
 |

 y M
y M
M0
 |
M’ 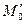
 0 x
0 x  x
x
На рисунке:
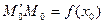
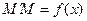
тогда 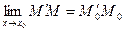 , т.е.
, т.е. 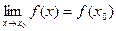
Возвращаясь к функции 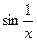 , можем сказать, что в точке
, можем сказать, что в точке  нарушается сразу 2 условия непрерывности (неопределенность в т.
нарушается сразу 2 условия непрерывности (неопределенность в т.  и не имеет предела в этой точке). Поэтому данная функция разрывна в т.
и не имеет предела в этой точке). Поэтому данная функция разрывна в т.  .
.
Возвращаясь к пример 2 видим, что для данной функции нарушается 3 условие непрерывности, поэтому функция разрывна.
Если бы мы придали функции  в точке
в точке  значение 2, то измененная таким образом функция оказалась бы непрерывной в т.
значение 2, то измененная таким образом функция оказалась бы непрерывной в т.  .
.
Свойства функций, имеющих пределы в данной точке.
(общие теоремы о пределах)
Теорема 1. (единственность предела).
Если  то
то  .
.
 Допустим противное, т.е.
Допустим противное, т.е.  . Выберем
. Выберем  , так, что бы окрестности т.
, так, что бы окрестности т. 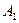 ,
, не пересекались, т.е.
не пересекались, т.е. 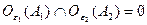 т.к.
т.к.  , то
, то 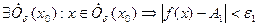 т.е.
т.е.  аналогично
аналогично 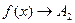 то
то 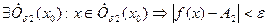 т.е.
т.е.  .
.
Рассмотрим 
Тогда,

 и
и 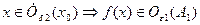 и
и 
 , что невозможно, т.к. указанные окрестности не пересекаются.
, что невозможно, т.к. указанные окрестности не пересекаются.
Теорема 2 (локальная ограниченность функции, имеющий предел).
Если предел  при
при 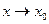 равняется А, то найдется окрестность
равняется А, то найдется окрестность  , во всех точках которых функция
, во всех точках которых функция  ограниченна.
ограниченна.
 Положим
Положим 
Из условия теоремы следует существование окрестности: 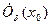 . Следовательно:
. Следовательно: 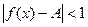

 Отсюда для указанных х
Отсюда для указанных х 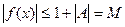
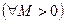 что и означает ограниченность
что и означает ограниченность  в
в 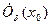 .
.
| ЛЕКЦИЯ № |
Свойства функций
(продолжение)
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 700; Нарушение авторских прав?; Мы поможем в написании вашей работы!