Сложность в среднем

Задачи

1. Для любого n eZ выполнено n = I ⁿ ₂ I + Г ⁿ ₂1, для любого a еЖ выполнено \a]=-[-a\.

2. Для любых k, n GN+, k > 1, выполнено Llog _k n\ + 1 = [log _k (n + 1)1.

Указание. Пусть m еN+ таково, что k^m-¹ Цn<k^m, тогда k^m-¹ <n + 1Цk^m. Прологарифмировать по основанию k обе системы неравенств.

3. Предположим, что в нашем распоряжении нет операции обмена
a <—> b и мы заменяем ее тремя присваиваниями:

c:=a; a:=b; b:=c;

чему в этом случае равны сложности первого и второго варианта сор­тировки простыми вставками по суммарному числу сравнений и при­сваиваний?

4. Пусть полином f(n) = a_mn^m +... + a₁n + a₀ имеет ненулевой
старший коэффициент a_m. Тогда

а) f (n) = O (n^k)<=> k:? m,

б) f (n) = n(n^k)<=> k ^ m,

в) f (n) = 6(n^k)<=> k = m, при k = m также выполнено f(n)~a_mn^m.

Подробнее об аддитивных цепочках см. в [19, разд. 4.6.3].

Задачи

5. Пусть Р(п)—количество простых множителей целого числа п > 1 с учетом кратности. Имеет место точная оценка Р{п) = О (log п).

6. (Продолжение предыдущей задачи.) Пусть

Р*(т)= шах Р(п),

т = 2,3,... Верно ли, что P *(m) = 6(m)?

7. Указать все вещественные значения 5, при которых справедлива
оценка

а) T_TD(n) = 0(.n⁵),

б) Г_тп(п) = П(п⁵),

в) r_TD(n) = 6(n ⁵),

где T _TD(n)—сложность алгоритма пробных делений (пример 1.2).

8. Железнодорожный сортировочный узел устроен так, как пока­
зано на рис. 6. На правой стороне собрано некоторое число вагонов

МИМО

вСЗСТИ»

тупик

Рис. 6. Сортировочный узел.

двух типов (на рис. 6—черные и белые), по п штук каждого типа. Ту­пик может вместить все 2п вагонов. Требуется, пользуясь тремя сорти­ровочными операциями В, ИЗ, МИМО, собрать вагоны на левой сто­роне так, чтобы типы вагонов чередовались. Указать такой алгоритм решения этой задачи, сложность которого по числу сортировочных операций при рассмотрении п в качестве размера входа равнялась бы Зп-1.

9. Хорошо известно, что мультипликативная сложность метода Гаусса решения системы п линейных уравнений с п неизвестными допускает оценки

1) 0(п³), 2)|п³+0(п²), 3) в(п³).

38 Глава 1. Сложности алгоритмов как функции числовых аргументов

а) Из какой оценки (указать номер) следуют две остальные?

б) Можно ли из приведенных оценок выбрать такую, которая яв­
ляется следствием любой из остальных?

в) Является ли оценка П(п³) следствием какой-либо из оценок 1,
2, 3?

10. Для сложности T q_S (п) быстрой сортировки выполняется оценка
T _QS(n) = в(п²). (Обозначение QS происходит от английского названия
быстрой сортировки —quick sort.)

Указание. Оценка T _QS(n) = fi(n ²) устанавливается предъявлением приме­ра. Неравенство T_QS(n)<n² можно доказать индукцией по п, используя то, что при фиксированном n eN⁺ квадратичная функция (т - I)² + (п - т)² от т принимает на отрезке [1, п ] свое максимальное значение в одном из концов этого отрезка.

11. Алгоритм, использующий только аддитивные операции и срав­
нения целых чисел для проверки того, является ли данное целое по­
ложительное п точным квадратом, может быть основан на вычисле­
нии последовательности значений 1,1 + 3,1 + 3 + 5,... до появления
в ней первого большего или равного п элемента. Сложность по числу
аддитивных операций и операций сравнения этого алгоритма (назо­
вем его sq_x) допускает оценку 6 (л/п). Сохранится ли эта оценка, если
дополнительно использовать операцию нахождения целой части по­
ловины числа (считается, что затратность этой операции такая же,
как у аддитивных операций) для того, чтобы предварительно выяс­
нять, на какую максимальную степень двойки — четную или нечет­
ную—делится п (алгоритм sq₂)?

12. (Продолжение предыдущей задачи.) Пусть T _sqi(n), T _sq2(n) —
сложности, соответственно, первого и второго вариантов рассмотрен­
ного алгоритма и

Т* ( т )= max T_sa(n), Г* (m) = max T_sa (n),

m = 2,3,...

а) Как связаны значения функций T _s*_qi(m) и T _s*₂(m)?

б) Имеются ли среди оценок 6(m), O (log m), в(2^{т / 2}), 0(2^т) такие,
которые верны для T _s*₂(m), и если да, то какие именно?

13. Изменим в алгоритме Грэхема (пример 3.1) этап удаления
вдавленных вершин: будем обходить — возможно, многократно —
против часовой стрелки вершины построенной несамопересекающей-
ся ломаной и удалять вдавленные вершины до тех пор, пока при
очередном обходе не окажется безуспешной попытка найти хотя бы

Задачи

одну вдавленную вершину. Сложность этого варианта рассматривае­мого этапа алгоритма Грэхема есть Г2(п²), где п — начальное число вершин ломаной (в то время как сложность этого этапа в алгоритме Грэхема есть 0(п)).

14. Рассмотрим в главных чертах алгоритм Шеймоса—Хоя¹ по­строения пересечения Р n Q двух выпуклых многоугольников Р и Q содержащих соответственно Z и т вершин. Считаем, что многоуголь­ники задаются массивами P₁,P₂,...,Pi и Q i, Q ₂, •••j Qm координат сво­их последовательных вершин.

Упорядочим множество всех абсцисс обоих многоугольников по возрастанию (для простоты считаем, что абсциссы попарно раз­личны, хотя это и несущественно), в результате получим абсциссы а_г < а ₂ <... < а_{1 + т} (рис. 7). Теперь для каждого i = 1, 2,..., Z + т - 1

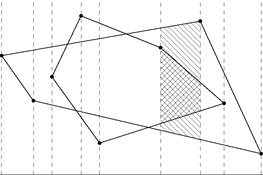
a ₁ a ₂ a ₃... a_i a_{i +1}... a_{m + l}

Рис. 7. Алгоритм Шеймоса—Хоя (1 = 5, т = 4).

строим пересечение трапеций, вырезаемых прямыми x = a_t,x = a_i+1 в заданных многоугольниках. (В вырожденном случае такая трапе­ция превращается в треугольник.) Из получившихся пересечений трапеций можно собрать Р n Q, удаляя лишние вершины.

Привлекая дополнительно те или иные структуры данных (масси­вы, списки,...) и уточняя по мере надобности какие-то этапы алго­ритма, добиться того, чтобы в итоге алгоритм (обозначим его бук­вами SH) имел следующие сложностные характеристики. Если раз­мер входа — это г = 1 + т, то T _SH(r) = 6 (г); если размер входа — это s = max{Z, т}, то r_s'_H(s) = 6(s); если размер входа имеет два параметра

См. [30, гл. 7].

40 Глава 1. Сложности алгоритмов как функции числовых аргументов

I и т, то Tg'_ti(l,m) = Q(l + m) —мы рассматриваем операции сравне­ния и перемещения элементов, арифметические операции, как муль­типликативные, так и аддитивные, все вместе. Для пространственной сложности— S _SH(г), S'_SH(s) или S '^a, т) в зависимости от выбора раз­мера входа — получаем те же оценки в(г), 6(s) или 6(Z + m).

Указание. Если исходные многоугольники представить, например, двуна­правленными списками координат последовательных вершин, то список абс­цисс (а₁,а₂,...,а_!+т), а_г < а₂ <... < а_1+т, можно получить с временными за­тратами, не превосходящими с₀(1 + т).

При определении пространственной сложности можно заметить, что об­щее число вершин искомого пересечения не превосходит 3(1 + т) —это сле­дует непосредственно из самого алгоритма Шеймоса—Хоя: при построении пересечения двух трапеций может возникнуть не более двух дополнительных вершин.

15. Расширить алгоритм построения вояжа в ориентированном графе G = (V, Е) с выделенной начальной вершиной v (пример 3.2) так, чтобы помимо вояжа алгоритм выдавал также информацию о том, охватил ли вояж все ребра графа. Размер входа имеет два параметра m =| V |, п = \Е\. Для графов, не содержащих изолирован­ных вершин, т. е. вершин, подобных вершине 7 на рис. 3, сложность расширенного алгоритма должна быть 0(,п).

16. Задача распознавания существования и фактического построе­ния эйлерова цикла в данном графе для ориентированного случая вы­глядит так: выяснить, имеется ли в данном ориентированном графе цикл, проходящий по всем ребрам графа по одному разу, и если су­ществует, то построить этот цикл. Воспользовавшись рассмотренным алгоритмом построения вояжа (пример 3.2), дать алгоритм решения этой задачи. Размер входа имеет два параметра m= \V\, п = \Е\. Для графов, не содержащих изолированных вершин, сложность предлага­емого алгоритма должна быть 0(,п).

17. Путник столкнулся со стеной, простирающейся бесконечно в обе стороны. Имеется дверь в этой стене, но путник не знает ни расстояния до двери, ни направления к ней. Предложить позволя­ющий добраться до двери алгоритм, сложность которого допускает оценку 0{п), где п — число шагов (неизвестное путнику), изначаль­но отделяющее путника от двери.

Указание. Сумма s_k = 1 + q +... + q^k, q > 1, есть величина порядка q^k, т.е.s_k = e(q^k).

18. Будем считать затратностью любого построения на плоскости
с помощью циркуля и линейки количество линий (окружностей или

Задачи

прямых), проводимых в ходе построения. Рассмотрим задачу постро­ения отрезка, длина которого равна 1 / п от длины исходного отрезка, считая п размером входа. Предложить для этой задачи такой алго­ритм решения, сложность которого допускает оценку O (log n).¹

19. При п = 15 возможно вычисление а^п с меньшим числом умно­жений, чем требуется бинарному алгоритму возведения в степень.

20. Пусть двоичная запись числа n eN есть ft...ft/Зо. Алгоритм

и:=1;

for i = k downto 0 do

и:=и-и;

if Pi = l then u:=u-afi od

вычисляет aⁿ. Сравнить сложность этого алгоритма по числу умно­жений с аналогичной сложностью бинарного алгоритма возведе­ния в степень, рассмотренного в примере 4.2, при использовании п или соответственно т = А(п) в качестве размера входа. (Описанный в этой задаче алгоритм является еще одним вариантом бинарного алгоритма возведения в степень.)

21. Для функции Z(n), определенной в конце § 4, выполнено 1{аЪ) s= sSZ(a)+Z(b)-l для всех a, b eN+.

22. (Продолжение предыдущей задачи.) Можно ли утверждать, что Z(ab) = Z(a)+Z(b)-l для всех a, b eN+?

¹ Разбор задач на построение с точки зрения их сложности содержится, например, в [11, §15].

Глава 2

Дата добавления: 2014-01-11