Функции, убывающие по ходу выполнения алгоритма

Часто выполнение алгоритма является последовательностью однотип­ных шагов (итераций). Если все шаги равнозатратны по времени, то общее их число с точностью до постоянного множителя эквивалентно временным затратам рассматриваемого алгоритма для данного вхо­да, и важной задачей является определение или хотя бы оценивание числа этих шагов.

Пример 9.1. Пусть а₀, а₁ —натуральные числа, а₀^а₁. Поиск наи­большего общего делителя (нод) чисел а₀, а₁ по алгоритму Евклида требует выполнения серии однотипных шагов, каждый из которых— деление с остатком:

a₀ = q₁a₁ +а₂, а₁ = q₂a₂ +а₃,

(9.1) а_п-3 = Чп-2а_п-2 + а_п- 1

a „-2 = q n -1 a „-1 + a n,

^ап-1 = Чп^ап.

В этом случае а_п = нод(а₀, а₁), так как

нод(а₀, а₁) = нод(а₁, а₂) =... = нод(а_п, 0) = а_п.

Последовательность получаемых остатков убывает (остаток меньше делителя), при этом все остатки — неотрицательные целые. Не су­ществует убывающей бесконечной последовательности, элементами которой являются неотрицательные целые числа, поэтому выполне­ние алгоритма Евклида (будем обозначать его буквой E) завершается для любых натуральных а₀, а ₁, и число делений с остатком не пре-

§ 9. Функции, убывающие по ходу выполнения алгоритма 75

восходит а_г. Обозначив через С_Е{а₀,а_г) исследуемое число делений с остатком, получаем

С_Е(.а₀,а₁)^а₁ (9.2)

(для упрощения записи мы пишем С_Е(,а₀,а_г) вместо С^{а₀, а_г)). Это говорит о том, что если а_г рассматривается как размер входа или ес­ли а₀, а_г рассматриваются как два параметра размера входа, то слож­ность алгоритма Евклида по числу делений не превосходит а_г. Как мы увидим, эта оценка является весьма грубой, но, привлекая сход­ные рассуждения, можно получать и более тонкие оценки.

Формализуем те соображения, которые привели нас к этой первой оценке. Каждый шаг алгоритма имеет дело с парой неотрицатель­ных целых {а_{__ъ a_t) и при условии a_t ф 0 перерабатывает эту пару в {a_ha_i+1), где a_i+1 равно остатку от деления а₍__г на a_t. На множе­стве пар неотрицательных целых чисел к, I мы определяем функцию L (fc,Z), принимающую неотрицательные целые значения. Эта функ­ция такова, что когда при выполнении алгоритма Евклида мы пере­ходим от пары {а_{__ъ a_t) к паре (а_ь a_i+1), значения функции убыва­ют: L{a_i_₁,a_i)>L{a_i,a_i+1). Так как функция целочисленна, то ее зна­чение убывает с каждым шагом по крайней мере на единицу. От­сюда следует, что общее число шагов не превзойдет значения функ­ции L на исходной паре чисел. Мы рассмотрели функцию L{k,l) = l, и это привело нас к выводу, что число шагов не превзойдет значения Ца₀,а₁)=а₁.

Для обоснования того, что число делений в алгоритме Евклида растет медленнее, чем а_ъ было бы достаточно найти соответствую­щую функцию I(fc,Z), значения которой при больших к,1 оказывают­ся существенно меньшими, чем Z. Эта функция по-прежнему должна быть определена для любых неотрицательных целых k,l, М Z, прини­мать неотрицательные целые значения и убывать при замене пары М парой I, г, где г — остаток от деления к на Z. Хотя бы одна па­ра целых неотрицательных k,l, к^1, должна обращать L (M) в нуль, иначе вместо L{k,l) можно взять функцию L '(M) = ДМ) - 1 и т.д.

Предложение 9.1. Пусть к,1&П⁺, к>1, и пусть г —остаток от деления к на I. Тогда

(i) A(fc) > А(г), где, как обычно, А(-) — битовая длина данного числа;

(ii) функция

L (M) = A(fc) + A(Z)-2 (9.3)

такова, что L (k, l) > L (l, r).

76 Глава 3. Оценивание числа шагов (итераций) алгоритма

Доказательство. (i) Имеем k = ql + r, q^l, откуда k ^ l + r > 2r. Следовательно, A(k) > A(r).

(ii) Из A(k) > А(r) следует A(k) + A(l) - 2 > A(l) + А(r) - 2. П

Очевидно, что функция (9.3) неотрицательна. Таким образом, справедлива оценка

C _Е(a ₀, a ₁)^А(a ₀)+А(a ₁)-2. (9.4)

Но если a ₀ очень велико в сравнении с a_г, то А(a ₀) + А(a _х) - 2 > a_г. Тем не менее, теперь для C_Е{a₀,a_г) уже легко выводится хорошая оценка. Пусть число делений с остатком больше 1. Имеем

C_Е(a₀, a_г) = C_Е{a_ъ a₂) + 1 s= Х{a_г) + А(a ₂) - 1 s= 2А(a _х) - 1.

Оценка

C _Е(a ₀, a ₁)^2А(a ₁)-1, (9.5)

очевидно, верна и в случае единственного деления: C_Е(a₀, a_г) = 1 при том, что \{a_г) ^ 1.

Если взять a_г за размер входа {a₀,a_г), то для сложности по числу делений будем иметь

T_Е{a_г) = шах C_Е(a₀, a) s= 2А(a _х) - 1 = 2Llog_? a j + 2 - 1 «S 2 logo a_г + 1.

Доказанное нами можно переформулировать так:

Если рассматривать a_г как размер входа a₀, a_г алгоритма Евкли­да, то для сложности T _Е(a _х) по числу делений выполнено неравенство

T _E(a ₁)^21og₂ a ₁ + l. (9.6)

Эта же оценка имеет место и при рассмотрении двух параметров a₀, a_г размера входа.

Для достаточно больших a_г верхняя оценка (9.6) существенно луч­ше, чем T_Е{a_г) s= a_г. (Несколько более точная, чем (9.6), оценка дается в задаче 52.)

Рассматривая далее оценки сложности по числу делений алгорит­ма Евклида, мы будем использовать значение a_г в качестве размера входа (значение a₀ может быть очень большим в сравнении с a_ъ но первое же деление с остатком приведет к a_г,a₂, где a₂ <a_г).

Известно, что алгоритм Евклида допускает разнообразные обоб­щения и расширения. Прежде всего, вместе с нод(a ₀, a_г) можно на­ходить целые s, t такие, что

sa ₀ + ta ₁ = HOfl(a _0j a ₁). (9.7)

§ 9. Функции, убывающие по ходу выполнения алгоритма 77

Чтобы это показать, обратимся к (9.1). Пусть уже известны a₀,a_ъ......, a_i, 1 ^ i ^ n - 1, и пусть для них найдены множители s ₀, t₀; s _ls t _x;......; si, ti такие, что

s₀a₀ + t₀a_г=a₀, s₁a₀ + t₁a₁=a₁,..., s_i-₁a₀ + t_i-₁a₁=a_i-₁, s_ia₀ + t_ia₁=a_i.

После выполнения очередного деления с остатком a_i-_г = q_ia_i + a_i+1 имеем a_i+1 = a_i-_x - q_ia_i и

(s_{i -}- q_is_ia o + C t_{i -}- q_it_ia ^ a ^.

Можем положить

s_i+1=s_i-₁-q_is_i, t_i+1 = t_i-₁-q_it_i, i = l,...,n-l; (9.8)

при этом

s ₀ = l, t ₀ = 0; s ₁ = 0, t ₁ = l. (9.9)

Решение поставленной задачи дают числа

s = s_n, t = t_n.

В процессе применения этого алгоритма к числам a₀ = 39, a _г = 15 возникают остатки 9, 6, 3, 0 и соответствующие ненулевым остаткам пары множителей суть 1, -2; -1, 3; 2, -5. Имеем 2 · 39 + (-5) ·15 = 3 = = нод(39,15).

Этот алгоритм мы назовем расширенным алгоритмом Евклида и будем его обозначать буквами ЕЕ, от его английского названия extended Euclidean—расширенный евклидов. Каждый шаг расширен­ного алгоритма Евклида содержит три мультипликативных опера­ции— одно деление с остатком и два умножения.

Если рассматривать a _г как размер входа a₀, a _г расширенного алго­ритма Евклида, то для мультипликативной сложности T _ЕЕ{ a _г ) этого алгоритма имеем T _ш{ a _г ) s= 6 log₂ a _г + 3.

Расширенный алгоритм Евклида дает возможность решать в це­лых числах линейные уравнения с целыми коэффициентами (см. за­дачу 56), он также играет существенную роль в модулярной арифме­тике (см. § 22).

Если дополнить расширенный алгоритм Евклида еще одним ша­гом, то получатся s_{n +1}, t_{n +1} такие, что

sn +i a o + tn +i a i = 0. (9.10)

Например, для a₀ = 39, a _г = 15 имеем s ₅ = -5, t ₅ = 13. Легко доказать, что

| s i|^| s ₂|^| s ₃|, | t i|^| t ₂| < | t ₃L (9.11)

78 Глава 3. Оценивание числа шагов (итераций) алгоритма

и при п>2

| s ₃| < | s ₄| <... < | s_{n +1}|, | t ₃| < | t ₄| <... < | t_{n +1}|. (9.12)

Несколько труднее, но также возможно доказать, что \s_t | и \t_t | взаим­но просты при i = 1, 2,..., п + 1 (см. задачу 57). Из (9.10) и взаимной простоты s_{n +1} и t_{n +1} следует

l sn +1l= нод(а₀,_а1), l^f"+1l= нод(а₀,_а1).

Вместе с (9.11), (9.12) это дает нам

I s JsSd1, \t_n\<a₀. (9.13)

Эти неравенства пригодятся нам в дальнейшем.

Пример 9.2. Бинарный поиск места (т. е. значения р, 1 ^ р ^ ^ п + 1,—как объяснено в приложении A) элемента у в упорядочен­ном массиве из п элементов х ₁ < х₂ <... < х_п:

р:=1; q:=п + 1; while p<q do

r:= I ^-^ I; if x_r<y then p:= r + 1 else q:=r fi od

Обозначим этот алгоритм буквами BS от его английского названия binary search—бинарный поиск. Будем считать число элементов сег­мента массива длиной этого сегмента (при рассмотрении задач сор­тировки и поиска мы называем сегментом массива любую упорядо­ченную часть x_s < x_s+1 <... < x_t_₁ < x_t данного массива). Легко видеть,

что от сегмента длины к мы переходим к сегменту длины 2 или

2 — 1. Это говорит о том, что с каждым шагом алгоритма функция L (fc) = A(fc), где положительное к является длиной сегмента, рассмат­риваемого на данном шаге, убывает по крайней мере на единицу, пока не приходим к сегменту, содержащему один элемент, после че­го еще одно сравнение полностью решает задачу. Отсюда сложность бинарного поиска не превосходит A(n) = Llog₂ п\ + 1. Мы видим так­же, что если у меньше минимального элемента рассматриваемого сегмента длины к > 1, то длина сегмента на следующем шаге будет

равна \-2\. Поэтому если изначально у <х ₁, то в ходе бинарного по­иска будут рассматриваться сегменты длины

^п l-l2 2, 2

n,₂ i2^,...,1

§ 9. Функции, убывающие по ходу выполнения алгоритма 79

соответственно (битовая длина каждого следующего элемента после­довательности на единицу меньше битовой длины предыдущего), и в целом потребуется в точности A(n) = Llog₂ n \ + 1 сравнений. Исполь­зуя утверждение, содержащееся в задаче 2, мы можем сформулиро­вать установленное свойство бинарного поиска так:

Сложность T_BS (n) бинарного поиска места элемента в массиве дли­ны n по числу сравнений равна Llog₂ n \ + 1, или, что то же самое, [log₂(n + l) l.

Выражение |"log₂(n + l) l для указанной сложности иногда бывает удобнее, чем Llog₂ n \ + 1, потому что оно имеет смысл и в вырожден­ном случае n = 0.

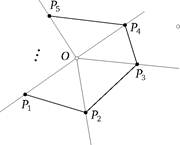
Бинарный поиск находит широчайшее применение при поиске ин­формации в разнообразных таблицах. Укажем здесь еще одно его применение, касающееся вычислительной геометрии: он позволяет быстро определять, принадлежит ли произвольная точка Q выпук­лому n -угольнику, заданному вершинами P_ЪP₂,...P_n. Можно легко построить какую-нибудь внутреннюю точку O данного n -угольника. В силу его выпуклости точка Q — внутренняя, если и только если Q и O лежат в одной полуплоскости относительно любой из прямых P_гP₂,...,P_n_₁P_n,P_nP₁. Это соображение приводит к имеющему времен­ную сложность 6(n) алгоритму. Но допустим, что проведены n доба­вочных лучей (рис. 12), исходящих из точки O и проходящих через

Q

Рис. 12. Точка Q лежит между двумя лучами, проведенными из внутренней точки O многоугольника через его вершины.

вершины (считаем, что O = Q, иначе мы сразу бы заключили, что Q принадлежит многоугольнику). Можно установить, какому из углов ∠ P ₁ OP ₂,..., ∠ P_{n 1} OP_n, ∠ P_nOP ₁ принадлежит точка Q: если углы прону-

80 Глава 3. Оценивание числа шагов (итераций) алгоритма

мерованы в указанном порядке, то бинарным поиском определяется номер m угла, 1 ^ m ^ n; при этом если Q лежит на одном из про­веденных лучей, то из двух значений m берется любое. Узнав m, мы проверяем согласованность расположения точек O и Q по отношению к прямой, являющейся продолжением той стороны многоугольника, концы которой лежат на сторонах m -го угла.

Теперь заметим, что в самом проведении лучей OP_ъOP₂,...,OP_n нет необходимости: сравнение Z.P_xOQ с LP_xOP_i требует ограниченно­го числа операций и в том случае, когда нам лишь известны коорди­наты точек O,Q,P₁,P_i.

Основывающийся на бинарном поиске алгоритм распознавания принадлежности точки выпуклому n-угольнику имеет сложность O (log n) по общему числу операций и пространственную сложность O (1).

Полезным для решения ряда задач является то обстоятельство, что если точка не принадлежит данному выпуклому n -угольнику, то с по­мощью этого алгоритма мы дополнительно определяем одну из сто­рон n -угольника, которая из этой точки видна целиком (рис. 13).

Q

Рис. 13. Для точки Q, не принадлежащей данному выпуклому n -угольнику, находим сторону n -угольника, которая из Q видна целиком.

Пример 9.3. Установим число этапов слияния при сортировке, предложенной Дж. фон Нейманом (которая является одним из вари­антов сортировки слияниями). При сортировке фон Неймана шаг за шагом происходят переброски элементов исходного массива в допол­нительный массив и наоборот, и каждая переброска сопровождает­ся слиянием соседних сегментов массива (рис. 14). В данном слу­чае в качестве вспомогательного размера массива удобно рассмот­реть k — число сегментов (первоначально k = n, затем, шаг за ша­гом, k довольно быстро убывает). При анализе бинарного поиска места элемента мы фактически использовали, что если 2 ^m ~¹ ^ k < 2^m,

§ 9. Функции, убывающие по ходу выполнения алгоритма 81

а) б) в)

Дата добавления: 2014-01-11