Качество оценок

После вывода оценки сложности алгоритма часто возникает вопрос о том, насколько эта оценка хороша и нельзя ли входящие в оцен­ку константы и функции заменить другими так, чтобы оценка стала более точной, и, как следствие, несущей больше информации об ис­следуемом алгоритме.

Пример 10.1. В примере 9.1 для сложности Т_Е{а_г) по числу деле­ний алгоритма Евклида мы легко получили верхнюю оценку а_ъ а за­тем, после некоторых усилий, пришли к логарифмической верхней оценке (9.6). Отвлекаясь от значений констант, перейдем от (9.6) к

r_E(a ₁) = 0(log a ₁). (10.1)

Нами пока не доказано, что оценка (10.1) является точной, и, как следствие, что не верна, скажем, оценка O{\f\oga₁) или CKloglog a ^) и т.д. Чтобы доказать точность (10.1), достаточно подобрать для ал­горитма Евклида последовательность входов

{а^,а^), (а™,а™),...

таких, что последовательность а^ (последовательность размеров вхо­да) неограниченно возрастает и С_Е(,а^\ а^) = f2(log a ^ ^{n )}) при п—><*>; тогда, очевидно, будем иметь Т_Е(а^) = U(loga^).

Фактически, нам нужна последовательность таких входов возрас­тающего размера, для каждого из которых алгоритм Евклида ра­ботает медленно. Подойдет, например, последовательность входов

84 Глава 3. Оценивание числа шагов (итераций) алгоритма

UWb F J, п = 0,1,..., где F q,^,^,... —числа Фибоначчи, определяе­мые равенствами F ₀ = О, F _x = 1 и правилом «каждое следующее чис­ло равно сумме двух предыдущих», т. е. рекуррентным соотношением Fn+2 = Fn+i +Fn. Из определения чисел Фибоначчи следует, что при­менение алгоритма Евклида к F_n+1,F_n при п ^ 1 требует п делений (все частные будут равны единице), поэтому C _E(F_{n +1}, F J = п.

По индукции доказывается, что для всех неотрицательных п спра­ведлива формула Бине:

J7 -_к(фл_(_ф)-л) (Ю.2)

V5

где

ф= ^{1 + A/g} = 1,61803...

(деление отрезка в отношении 1: ф называют золотым сечением). Так как ф > 1, то из (10.2) получаем

0" = _A/5 F_n (l+ o (l)), (10.3)

и, поскольку log₀(1 +о(1)) = о(1), с помощью логарифмирования (10.3) по основанию ф имеем

СеС^п+i» Рп) = п = log<p F_n + 0(1) = n(log F_n),

откуда следует, что оценка (10.1) точная. Мы докажем более сильное утверждение:

Т_Е{а₁)>^\о%_фа₁+_Г, (10.4)

где у— некоторая константа. Это вместе с (10.1) даст

r_E(a ₁) = e(log a ₁). (10.5)

Приступая к доказательству, мы перейдем от функции C _E(a ₀, a _i), имеющей два аргумента, к функции одного аргумента. Каждому вхо­ду (a _n, сь), a _n ^ сь > 0, мы сопоставим рациональное число г = — ^ 1, которое однозначно определяет число шагов алгоритма Евклида для

a _n, а-.. (Пусть - = ^, апиа, взаимно просты, a _n = ua _n, сь = ua -i; то-
uj i _Q^ a_t

гда остатки a ₂, a ₃,... и a ₂, a ₃,..., возникающие в ходе применения ал­горитма Евклида к а₀,а_г и соответственно к а₀,а_г, отличаются лишь множителем и.) Будем обозначать это число шагов через С'_Е{г). Таким

образом, если г = ^, то С'(г) = C _E(a ₀, a _i).

§ 10. Качество оценок

Для дальнейшего будет полезным следующее свойство чисел Фи­боначчи:

F_n -₁ F_{n +1} = (-1) ⁿ, n = 1,2,... (10.6)

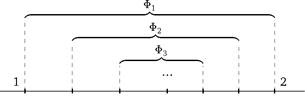
(доказывается индукцией по п). Рассмотрим вложенные отрезки Φ₁ э зΦрΦ₃э... числовой прямой:

f2„ f2„+1

п = 1,2,

Φ n

^ 2 п f2 +1 2 n -1, F 2n

Соотношение (10.6) позволяет установить, что ни один из этих

Очевидно, что

F 2n-1 F 2„

отрезков не пуст и что длина отрезка Φ _n равна

Φ₁ = [1, 2] (рис. 15). Далее можно доказать, что если рациональное

р ₂

F₄

Р ₆

Дата добавления: 2014-01-11