Булева арифметика

G

q^l взаимно просто с а"-^ч, так как а и q взаимно просты. Поэтому ко­эффициент при х" в левой части (22.3), равный (-l)ⁿ-^qaⁿ-^q(ⁿ), не

q

делится на q^l, следовательно, не делится наи поэтому не сравним
с 0 по модулю п. Мы доказали, что если п — составное, то сравне­
ние (22.3) не имеет места. □

Из предложения 22.2 следует, что для проверки простоты числа п можно взять любое а, взаимно простое с п (подходит, например, 1), и проверить (22.3). Но прямая такая проверка потребует П(п) = П(2^т) битовых операций, так как раскрытие скобок в левой части (22.3) дает п + 1 слагаемое. Алгоритм AKS предписывает проверку (22.3) по двум модулям

{х-а)^п=х^п-а (mod х^г - 1, п), (22.4)

г > 0. Сравнение (22.4) понимается в том смысле, что все коэффи­циенты остатка от деления полинома (х - а)" - х^п + а на х^г - 1 (они будут целыми числами) делятся на п. Вычисление остатков от деле­ния (х - а)" и х" на х^г - 1 производится с помощью бинарного ал­горитма возведения в степень, результат каждого умножения сразу же заменяется остатком от деления на х^г - 1. Но если взять произ­вольное г g N⁺, то может оказаться, что (22.4) выполняется и при некоторых составных п. Число г должно подбираться специальным образом, и авторы показывают, что подходящее для целей алгорит­ма г всегда существует и может быть выбрано без существенных за­трат так, что г = 0{т^ъ); после выбора г сравнение (22.4) надо прове­рить для «небольшого» числа «легко определяемых» а — количество этих а есть 0{-^гт). Итоговая сложность алгоритма допускает оцен­ку 0{т^1г). Заметим попутно, что в литературе по теории сложности часто используются оценки вида 0{f{m)) (О называется «О мягкое»),

Глава 5. Битовая сложность

за таким обозначением скрывается 0(/(m)log ^dm), где d — положи­тельное число, значение которого не уточняется. Авторы показывают, что битовая сложность их алгоритма допускает оценку 0{т^21/2), ука­зывая при этом, что если верны некоторые известные в теории чисел гипотезы (для которых имеются серьезные основания полагать, что они верны), то можно взять г = 0{т²), и в этом случае сложность алгоритма в целом есть 0{т^ь).

На этом мы завершим разговор об алгоритме AKS, добавив лишь ко всему сказанному, что, например, в криптографии практикуются вероятностные (типа Монте-Карло) алгоритмы распознавания про­стоты, имеющие меньшую сложность, но не исключающие появле­ния, хоть и с малой вероятностью, неверного ответа. В нашем курсе такого рода алгоритмы не рассматриваются¹.

Сложность булевых вычислений как сложность по числу булевых опе­раций может рассматриваться как алгебраическая сложность. Но ра­бота с булевыми величинами является фактически работой с бита­ми, и сложность по числу булевых операций в этом смысле совпа­дает с битовой сложностью. Таким образом, для алгоритмов булевой арифметики алгебраическая сложность по числу булевых операций и битовая сложность —это одно и то же. Аналогично дело обстоит и с пространственной булевой (= битовой) сложностью.

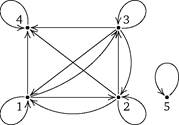
Пример 23.1. Пусть дан ориентированный граф G = {V, E),n = \V\. Пусть С = (су) — булева матрица смежности графа G: с_ц = 1, если и только если i -я вершина соединена ребром с j -й, i,j = 1, 2,..., п. Требуется построить для G его матрицу связности D = (d_{i ;}): d _y = 1, если и только если i = j или i -я вершина соединена путем из одного или более ребер с j -й, i,j = 1, 2,..., п. Если рассматривать G как граф некоторого бинарного отношения на множестве из п элементов, то задачу можно интерпретировать как задачу построения транзитив-но-рефлексивного замыкания данного бинарного отношения. Соот­ветственно, граф, для которого D является матрицей смежности, на­зывают транзитивно-рефлексивным замыканием графа G, а саму мат­рицу D — транзитивно-рефлексивным замыканием матрицы С. Для матрицы D используется обозначение С*. На рис. 20 показан ориен­тированный граф и его транзитивно-рефлексивное замыкание. Соот-

¹ По поводу этих алгоритмов распознавания простоты числа см. [21, гл. 33] и [8, гл. 4].

§ 23. Булева арифметика

б)

а)

2 Л 5

Рис. 20. а) Ориентированный граф; б) его транзитивно-рефлексивное замы­кание.

ветствующие матрицы C и C ^∗ выглядят следующим образом

С

°			л
о			о

С*

1			л
о

Нам понадобятся произведения булевых матриц, которые опреде­ляются как обычно: например, произведение F квадратных матриц A и B порядка n определяется формулой

fij = \/(a_ikAb_kj), i,j = 1,2,

k=i

Элемент с индексами i,j для краткости будем называть (i, Л-элемен-том матрицы.

Легко видеть, что С² = СлС— это матрица, для которой (i, j)-эле-мент равен 1, если и только если i -я вершина соединена с j -й путем длины 2 (т.е. состоящим из двух ребер). Аналогично, С^к— матрица, для которой (i, j)-элемент равен 1, если и только если i -я верши­на соединена с j -й путем длины к. Пусть / — матрица, для которой (i, Л-элемент равен 1, если и только если i = j. Тогда

c*=ivcvc²v...vcⁿ-\

Индукцией по к несложно доказать, что для любой квадратной буле­вой матрицы С и натурального к выполнено

/V C v C ²V...V C ^fc = (7v C)^fc. (23.1)

Это дает нам

C* = (lv СУ-¹. (23.2)

Глава 5. Битовая сложность

Тривиальный способ умножения булевых (n х п)-матриц требует в(п³) битовых операций. Если используется именно этот способ, то оценка числа операций для формулы (23.2) есть в(п⁴). Приме­нение бинарного алгоритма (пример 4.2) для возведения в степень булевой матрицы С позволяет перейти к оценке

6(n ³log n). (23.3)

Если нежелательно связывать основанный на формуле (23.2) алго­ритм построения транзитивно-рефлексивного замыкания с конкрет­ным способом умножения матриц, то верхнюю оценку числа битовых операций можно записать как

n + B (n)(A(n)+A*(n)-2), (23.4)

где В{п) — сложность используемого алгоритма умножения булевых (п х п)-матриц; слагаемое п отражает расход на сложение с матри­цей I.

Рассмотренный пример высвечивает связь задачи построения транзитивно-рефлексивного замыкания ориентированного графа с за­дачей умножения булевых матриц. Эта связь оказывается очень тес­ной, о чем мы еще будем говорить в § 28.

В следующем примере задача построения транзитивно-рефлексив­ного замыкания решается без использования умножения булевых матриц.

Пример 23.2. Исследуем сложность алгоритма С. Уоршелла, пред­назначенного для построения матрицы С*. В процессе применения этого алгоритма матрица С* строится за n = | V | шагов, после fc-го шага получается матрица D ^(fc) = (d?⁵), и d?) = ^ если и только если i -я вершина соединена таким путем с j -й, номера всех промежуточ­ных вершин которого не выходят за пределы множества {1,2,..., А:}. Вначале полагаем D ⁽⁰⁾ =/ V С. Затем для каждого к = 1, 2,..., п нахо­дим D «:

d^m = d *^_1) V (d (,^fc~^u Л d *^_1)). (23.5)

у у i fc kj ^K

После этого C* = D⁽ⁿ\

Формула (23.5) отражает то, что путь из i -й вершины в j -ю, все промежуточные вершины которого принадлежат {1,2,..., А:}, суще­ствует, если и только если реализуется хотя бы одна из следующих возможностей:

• имеется путь из i -й вершины в j -ю, все промежуточные вершины которого принадлежат {1, 2, ...,к - 1};

§ 23. Булева арифметика

• имеются пути из i -й вершины в k -ю и из k -й в j -ю, все промежу­точные вершины которых принадлежат {1, 2,..., k - 1}.

На вычисление D ⁽⁰⁾ уходит n битовых операций, вычисление каж­дой из матриц D^{(k )}, 1^k^n, требует 2n² операций. Итого, требуется 2 n ³ + n операций.

Алгоритм Уоршелла вычисляет матрицу C*, т. е. строит транзи-тивно-рефлексивное замыкание ориентированного графа G с n верши­нами, заданного матрицей смежности, затрачивая 2 n ³ + n битовых операций.

Алгоритм Уоршелла можно легко реализовать так, что храниться в памяти будут только D ^{( k} -¹⁾ и D ^{( k )}. Но на самом деле алгоритм Уор­шелла позволяет производить все вычисления, расходуя всего n² би­тов под хранение матричных элементов. Если мы вычислим D = I V C, а затем n раз обновим матрицу D (каждый раз всю целиком, не оставляя незатронутых элементов), используя на k -м этапе обновле­ния матрицы D присваивания

d_ij:= d_ij V(d_ik A d_kj),

k = 1,2,...n, то получим искомую матрицу связности. В самом деле, индукцией по k можно доказать, что после k -го этапа обновления по­лучаем матрицу, равную D ^{( k )}, при этом индуктивный переход от k - 1 к k основывается на том, что имеют место очевидные соотношения

dik dik, dkj dkj

k = 1, 2,..., n, т.е. при обновлении элемента d_ij на k -м этапе не име­ет никакого значения, был ли уже обновлен какой-то из элементов d_ik, d_kj или нет.

Если строить матрицу C * на месте исходной матрицы C, то алго­ритм можно изобразить так:

for l = 1 to n do c_ll:=1 od; for k =1 to n do for i = 1 to n do for j = 1 to n do

c_ij:= c_ij V(c_ik A c_kj) od od od

Подводя итог рассмотрению алгоритма Уоршелла, заметим, что, как и алгоритм Евклида в расширенной версии, он дает довольно

Глава 5. Битовая сложность

редкий пример, когда низкие временные затраты сочетаются с малым расходом памяти.

Алгоритм Уоршелла построения замыкания ориентированного графа имеет битовую временную сложность 2 n ³ + n, где n = \ V \ — чис­ло вершин графа. Пространственная сложность этого алгоритма ограничена константой.

При рассмотрении | V |, | E | в качестве двух параметров размера входа сказанное сохраняет силу, так как затраты алгоритма Уоршелла не зависят от числа ребер заданного входного графа.

Дата добавления: 2014-01-11