Линейная сводимость и нижние границы сложности

Нижеприведенная теорема является следствием определения 28.1.

Теорема 29.1. Пусть задачи P и Q таковы, что P s= Q. Пусть f (n) — асимптотическая нижняя граница сложности алгоритмов ре­шения задачи P, и при этом соотношение P^Qустанавливается без

§ 29. Линейная сводимость и нижние границы сложности 191

наложения ограничений на сложность алгоритмов решения задачи Q. Тогда f (n) является асимптотической нижней границей сложности алгоритмов решения задачи Q.

Доказательство. Для каждого алгоритма A_Q решения задачи Q
найдется такой алгоритм A_P решения задачи P, для которого T_A (n) =
= O(T_AQ (n)), или, эквивалентно, T_AQ (n) = П(T_AP (n)). Но T_AP (n) =
= П(f (n)), следовательно, T_AQ (n) = П(/(n)). П

Если при соблюдении условия этого предложения для какого-то алгоритма A_Q решения задачи Q имеет место оценка T_A (n) = = O (f (n)), то этот алгоритм будет оптимальным по порядку слож­ности и T_A (n) = в(f (n)). (При наличии ограничений на сложность

q

алгоритма A_Q, когда фактически предполагается, что A_Q принадле­жит некоторому классу J2, речь должна бы идти об оптимальности по порядку сложности в классе 21; но если ограничения таковы, что в класс £2. попадают наиболее рациональные алгоритмы, то упоми­нание класса Ш не обязательно.)

Пример 29.1. Вновь рассмотрим задачу построения выпуклой обо­лочки конечного множества точек с помощью арифметических опера­ций и сравнений. Многоугольник, являющийся выпуклой оболочкой, представляется массивом своих вершин в порядке их следования при обходе в некотором направлении, обычно против часовой стрелки, начиная с некоторой вершины. Мы покажем, что задача сортировки массивов вещественных чисел с помощью арифметических операций и сравнений линейно сводится к задаче построения выпуклой обо­лочки в этой постановке, считая, что в этих задачах затраты изме­ряются общим числом арифметических операций и сравнений. Но если порядок вершин выпуклой оболочки, которую надо построить, может быть произвольным, то задача меняется, и про нее мы ничего не утверждаем.

Пусть x₁,x₂,...,x_n — данный массив попарно различных веще­ственных чисел. Решив задачу построения выпуклой оболочки мно­жества точек с координатами

(x ₁, x²₁), (x₂,x ₂² ),..., (x_n,x_n²)

(см. рис. 23), мы можем, двигаясь по вершинам построенного много­угольника, найти вершину с наименьшей абсциссой, а затем постро­ить массив вершин в порядке возрастания абсцисс. Сложность этой дополнительной части работы допускает оценку O(n). Легко видеть, что сложность любого алгоритма построения выпуклой оболочки не

Глава 7. Сводимость

У >i

х

Рис. 23. Сведение сортировки чисел x_t,x₂, ■■■,х_п, отмеченных на оси абсцисс, к построению выпуклой оболочки точек (х_их*), {х₂,х\),..., {х_п,х²_п).

может быть меньше чем п. Таким образом, каждому алгоритму А построения выпуклой оболочки мы сопоставляем алгоритм сортиров­ки со сложностью 0{Т_А{п)). Следовательно, задача сортировки веще­ственных чисел с помощью арифметических операций и сравнений линейно сводится к задаче построения выпуклой оболочки.

Из результатов § 14 следует, что любая сортировка с помощью сравнений массивов длины п имеет сложность не менее log₂ п\. Но при построении выпуклой оболочки используются как сравнения, так и арифметические операции. Можно ли, привлекая помимо опера­ций сравнения еще и арифметические операции, предложить алго­ритм сортировки массивов вещественных чисел, сложность которого по числу сравнений была бы меньше, чем log₂ п\, пусть даже при том, что потребовалось бы очень большое число арифметических опера­ций? Ниже мы обосновываем отрицательный ответ на этот вопрос.

Дополнительное использование четырех арифметических опера­ций означает, что сравниваться могут не только числа х_ъх₂, ■■■,х_п, заданные изначально, но и значения рациональных функций от этих чисел. В качестве знаков сравнения могут использоваться

<, >, =, ф_у ^,;>.

Каждая рациональная функция F{х_ъ х₂, ■ ■ ■, х_п) записывается как отношение двух полиномов

р(х₁,х₂,...,х_п)

(29.1)

q(x₁,x₂,...,x_n)

F(x₁,x₂,...,x_n)

§ 29. Линейная сводимость и нижние границы сложности 193

(в этом параграфе мы рассматриваем рациональные функции и полиномы с вещественными коэффициентами). Каждый полином f (x ₁, x₂,..., x_n) можно рассматривать как рациональную функцию

f(x₁,x₂,...,x_n)
1.

Предполагается, что если алгоритм предписывает сравнение, в кото­ром участвует значение рациональной функции (29.1), то ее знамена­тель q(x₁,x₂,...,x_n) не обращается в 0 при рассматриваемых значе­ниях x ₁, x₂,...,x_n. Неравенство F₁(x₁,x₂,...,x_n)<F₂(x₁,x₂,...,x_n) рав­носильно, очевидно, неравенству F (x ₁ ,x₂,...,x_n) <0, где

F(x₁,x₂,...,x_n)=F₁(x₁,x₂,...,x_n)-F₂(x₁,x₂,...,x_n).

То же самое для сравнений со знаками >, =, ф, ^, ^.

Далее будут использоваться два свойства рациональных функций:

(R1) Множество точек (x ₁, x ₂,..., x_n)еГ, для которых данная ра­циональная функция (29.1) неопределена или равна нулю, является замкнутым; в свою очередь, те точки, в которых эта функция опреде­лена и имеет значение большее (меньшее) нуля, образуют открытое множество. Это следует из того, что рациональная функция непре­рывна на своем множестве определения.

(R2) Если рациональная функция (29.1) определена и равна нулю всюду на некотором непустом открытом подмножестве множества Ж ⁿ, то ее числитель p (x ₁, x₂,..., x_n) является нулевым полиномом (см. за­дачу 147).

Предложение 29.1. Функция f (n) = [log₂ n!] является нижней гра­ницей сложности по числу сравнений алгоритмов сортировки масси­вов длины n попарно различных вещественных чисел c помощью срав­нений и четырех арифметических операций.

Доказательство.^г Каждой из перестановок a = (a ₁, a₂,..., an)еП n сопоставим сектор S_a — подмножество пространства Ж n такое, что (x ₁ ,x₂,..., x_n) e S_a, если и только если числа x ₁, x₂,...,x_n попарно раз­личны и их относительный порядок совпадает с относительным по­рядком чисел a₁,a₂,...,a_n. Любой сектор является открытым множе­ством в Ж n. Каждому массиву вещественных чисел с попарно раз­личными элементами x ₁, x₂,...,x_n соответствует точка некоторого

!Идея элементарного доказательства сообщена автору С.П.Поляковым. Наиболее раннее (довольно трудное для понимания) доказательство было опубликовано H. Фрид­маном в [49].

Глава 7. Сводимость

сектора пространства Ж". В примере 14.2 говорилось, что при фикси­рованном п любую сортировку массивов длины п можно представить в виде дерева, каждой не являющейся листом вершине v которого приписано сравнение вида x_t < х_;-, а выходящие из нее ребра име­ют метки 1 («да») и 0 («нет»); при этом каждому листу Z приписан набор х; ,х<,...,х;, где (b, i ₂,...,*„) — некоторая перестановка чисел 1,2,...,п.

Алгоритм сортировки массивов длины п c помощью сравнений и четырех арифметических операций представляется деревом D, которое можно считать таким, что каждой не являющейся ли­стом вершине v приписано сравнение F_v(x₁,x₂,...,x_n) с нулем, где Р_у(х_ъх₂,...,х_п) — некоторая рациональная функция, а выходящие из вершины ребра имеют метки 1 («да») и 0 («нет»). При этом каждому листу Z приписаны рациональные функции

G_ll{x₁,x₂,...,x_n), G_l2{x₁,x₂,...,x_n),..., G_ln(x₁,x₂,...,x_n), (29.2)

значения которых для исходных х_ъх₂,...,х_п определяют требуемый

порядок X;, X;,...,Х;:

х = G,₁(x ₁, x ₂,..., x_n), х = G,₂(x ₁, x ₂,..., x_n),

- = G, _n (x ₁, x ₂,..., x_n).

Можно считать, что числитель каждой из функций F_v (x _l5 x ₂,...,х_п) не является нулевым полиномом, — в противном случае вершину v можно было бы удалить из дерева вместе с выходящей из нее вет­вью, начинающейся с помеченного единицей ребра. Множество JV тех точек Ж", в которых обращается в нуль числитель хотя бы одной из рациональных функций F_v (x _l5 x ₂,...,х_п), в силу свойства (R1) явля­ется замкнутым, причем это множество не может покрывать целиком ни один из секторов. Иначе в силу свойства (R2) произведение всех числителей рассматриваемых рациональных функций было бы нуле­вым полиномом, а это означало бы, что один из сомножителей этого произведения—нулевой полином.

Таким образом, каждое из множеств

S; = S;\JV, i = l,2,..., n!,

есть непустое открытое множество. Покажем, что для массивов, соот­ветствующих точкам из S'_t, i = l,2,..., п\, рассматриваемая сортировка в худшем случае требует не менее [log₂ n!l сравнений.

§ 30. Классы P и NP

Будем говорить, что точка (x _ъ x ₂,..., x_n) некоторого сектора со­гласуется с листом l дерева D, если соответствующая дереву D сор­тировка массива x _ъ x ₂,..., x_n заканчивается в листе l.

В том случае, когда D имеет не менее n\ листьев, мы, рассуждая так же, как в примере 14.2, получаем, что высота дерева D (слож­ность сортировки по числу сравнений) не может быть меньше чем [log₂ n\]. Допустим, что число листьев дерева D меньше чем n\. Тогда найдется лист l такой, что имеются точки в двух разных множествах S[, S'j, согласующиеся с l. В силу свойства (R1) найдутся непустые открытые множества U_г с S[, U₂ с S ' такие, что любая точка, принад­лежащая какому-то одному из них, согласуется с листом l. Если ли­сту l приписан массив (29.2), то для некоторых целых k,s, t, не мень­ших единицы и не превосходящих n, таких, что s^t, будем иметь G_k (x ₁, x ₂,..., x_n) = x_s при (x₁,x₂,...,x_n)&U₁ и G_k (x ₁, x ₂,..., x_n)= x_t при {x_ъx₂,...,x_n)&U₂. Но значения рациональной функции на одном из множеств U_ъ U₂ однозначно определяют значения этой рациональ­ной функции всюду на U_г и U₂ (это выводится из свойства (R2)), поэтому из того, что, например, G_k (x _ls x ₂,..., x_n) = x_s на U_ъ следует, что G_k (x _l5 x ₂,..., x_n) = x_s на U₂. Но мы знаем, что G_k (x _l5 x ₂,..., x_n) =x_t на U₂. Так как s / t, то в любом секторе x_sфx_t, в частности, это так и в секторе, подмножеством которого является U₂. Противоречие. □

Из доказанного предложения следует, что f (n) = n log n является асимптотической нижней границей сложности алгоритмов сортиров­ки массивов длины n попарно различных вещественных чисел c по­мощью сравнений и четырех арифметических операций. По теоре­ме 29.1 эта функция является также асимптотической нижней оцен­кой для алгоритмов построения выпуклой оболочки.

Любой алгоритм построения выпуклой оболочки с помощью арифметических операций и сравнений, который имеет сложность O (n log n), является оптимальным по порядку сложности по общему числу операций, и его сложность есть G(n log n). Алгоритм Грэхема построения выпуклой оболочки (пример 3.1) является оптималь­ным по порядку сложности по общему числу операций, коль скоро используемая им сортировка имеет сложность O (n log n) по числу сравнений.

§ 30. Классы Р и NP

Цель этого и следующих параграфов—дать общее, без многих дета­лей, представление о некоторых проблемах, касающихся алгоритмов

Глава 7. Сводимость

полиномиально ограниченной сложности (см. § 5, определение 5.2) или, другими словами, полиномиальных алгоритмов.

Подход, согласно которому алгоритмы подразделяются на поли­номиальные и все остальные, далеко не всегда является продуктив­ным с практической точки зрения (алгоритм со сложностью п¹⁰⁰, где п —размер входа, вряд ли найдет массовое применение), но при бо­лее широком взгляде этот подход имеет свою логику. Если для ре­шения важной задачи никак не удается найти алгоритм, сложность которого хотя бы при каком-нибудь показателе d допускала бы оцен­ку 0{n^d), то сам вопрос о существовании такого алгоритма нельзя назвать праздным.

Иногда бывает очень трудно установить принадлежность или со­ответственно непринадлежность задачи классу P, состоящему из та­ких задач, для которых существует полиномиальный алгоритм ре­шения. В классе P выделяют подкласс Р тех вычислительных задач, где результатом может быть лишь 1 или 0, т. е. фактически «да» или «нет», что типично для задач распознавания. К этим задачам относит­ся, например, задача распознавания выполнимости булевой форму­лы, задача распознавания существования в графе гамильтонова цик­ла и т. д. Неизвестно, существуют ли полиномиальные алгоритмы их решения, но сравнительно легко устанавливается их принадлежность специальному классу NP. Определение класса NP будет дано ниже, из него будет следовать, что Р с NP. Если бы было доказано, что Р = NP, то в широком спектре случаев мы бы легко устанавливали принад­лежность задачи распознавания классу Р, т. е. устанавливали бы су­ществование полиномиального алгоритма распознавания; его разра­ботка—это отдельный вопрос. Но равенство P = NP по сей день не доказано, и есть основания подозревать, что оно неверно. Возникает проблема Р = NP, о которой мы тоже будем говорить.

Вначале скажем о ряде ограничений, налагаемых на рассматрива­емые задачи. Во-первых, речь будет идти о задачах распознавания тех слов в данном алфавите Л, которые принадлежат оговоренному под­множеству (языку) L множества всех слов Л* в этом алфавите. Все объекты, о которых идет речь в рассматриваемых задачах, должны быть представлены (закодированы) словами в алфавите Л, входом алгоритма является одно-единственное слово в алфавите Л. Размер входа х —это всегда длина |х| (число букв) в слове х. Вычислитель­ные затраты должны учитываться достаточно тщательно, неучтенной может оставаться лишь незначительная часть операций (во всяком случае, допускающая полиномиальную верхнюю оценку). Если име­ется в виду модель вычислений РАМ, то предполагается, что вычисле-

§ 30. Классы PuNP

ния выполняются на базе конечного множества операций с тем или иным числом операндов, преобразующих буквы алфавита Л в буквы алфавита Л; исследуется сложность по числу этих операций — подо­бие битовой сложности. Требуется также учет числа присваиваний в ходе выполнения алгоритма.

Таким образом, содержательная задача распознавания (например, задача существования пути с фиксированными свойствами в задан­ном графе) должна быть для обсуждения ее принадлежности классам Р и NP переформулирована в виде задачи распознавания принадлеж­ности заданного слова некоторому языку. Такая формализация необ­ходима потому что одна и та же математическая идея при одном из двух разных способов представления данных может приводить к по­линомиальному алгоритму, а при другом—нет.

Часто при обсуждении проблемы Р = NP исходят из машины Тью­ринга (МТ) как модели вычислений, при этом вычислительные за­траты измеряются числом тактов работы машины. Это связано с тем, что модель МТ удобнее модели РАМ при доказательстве разного ро­да теорем об алгоритмах, в особенности — теорем о невозможности алгоритмов с теми или иными свойствами. Но модель РАМ ближе, чем МТ, к реальным вычислительным устройствам, и хотелось бы, чтобы результаты исследования классов Р и NP, проводимые на ос­нове модели МТ, сохраняли свою значимость для модели РАМ. Их значимость действительно сохраняется, о чем будет сказано в конце этого параграфа, а до той поры мы, как правило, не будем делать уточнений относительно модели вычислений. Но, повторяем, опера­ции преобразования букв, входящих в слова, должны подсчитываться тщательно.

По сути дела, в каждой задаче распознавания принадлежности слова языку L обсуждается некоторый предикат и(х), областью опре­деления которого является все множество Л*, и и (х) = 1, если и толь­ко если х е L. В дальнейшем нам часто будет удобно говорить не о языках, а о предикатах (по существу, это, конечно, одно и то же, но предикаты несколько предпочтительнее из-за того, что к ним можно применять логические операции, кванторы и т.д.). Соответственно, мы будем говорить о принадлежности предиката классу Р и т. д. Ино­гда нам будет удобно рассуждать о предикатах не одной, а нескольких таких переменных, которые принимают значения в Л*. В этих случа­ях без специального упоминания предполагается, что в алфавит Л включены некоторые разделители: если, скажем, разделитель «запя­тая» (т.е. «,») включен в Л, то v (x, у) имеет один аргумент х, у, где х и у суть слова в Л*, не содержащие разделителя «,» (кавычки по-

Глава 7. Сводимость

ставлены, чтобы не нарушать пунктуацию фразы). Соответственно, длиной пары слов x, y является | x | + | y\ + 1.

Теперь обсудим класс предикатов NP. Само его странное обо­значение NP есть не что иное, как аббревиатура от английских слов nondeterministic polynomial —недетерминированный полиноми­альный. Изначальное определение класса NP, появившееся в теории сложности в начале 70-х годов XX столетия, опиралось на понятие недетерминированного алгоритма¹. Позднее появилось эквивалент­ное определение, не прибегающее к недетерминированности.

Определение 30.1. Заданный на Л* предикат u (x) принадлежит классу NP, если существуют предикат R (x, y) е Р и полином p{n) та­кие, что u{x) можно представить в виде

u{x) = З _{y еЛ},_;| _{y К p (}| _x |) R x, y). (30.1)

В том случае, когда u (x) = 1, слово y называется сертификатом сло­ва x.

Пример 30.1. Булева формула f (x _l5 x ₂,..., x_n) выполнима, если су-

ществуют значения x °, x °,..., x_n ° g {0,1} переменных x_г,x₂,...,x_n та-

кие, что

f (x °, x °,..., x_n °) = 1;

в противном случае булева формула невыполнима. Так, булева фор­мула

­(­ x iV x a) (30.2)

выполнима, так как ее значение при x_г = 1, x ₂ = 0 равно 1, а булева формула x_г Л ­ x! одной переменной x_г невыполнима, так как и при x_г = 1, и при x_г = 0 значение этой формулы есть 0.

Любая булева формула может быть закодирована словом в алфа­вите

Л₁ = { x,0,1, (,),­, л, V},

для этого переменные x_г,x₂,x_ъ,... кодируются как x l, x 10, x ll,...: вслед за буквой x помещается номер переменной в двоичной систе­ме. Формула (30.2) кодируется как ­(­ x l V x lO), при этом, например, слово )xlx­ в алфавите А_г не является кодом какой-либо булевой формулы. Можно предложить простой алгоритм, который проверяет, является ли данное слово в алфавите Л_х кодом какой-либо булевой формулы, а также алгоритм, который по данному коду некой буле­вой формулы и данным булевым значениям (нулям и единицам) тех

См., например, [13].

§ 30. Классы PuNP

переменных, которые фактически присутствуют в этой формуле, на­ходит ее значение. На основе этих двух алгоритмов можно построить алгоритм, который по данному слову хёЛ* и слову у, являющему­ся конечной последовательностью нулей и единиц, проверяет, верно ли, что

(a) х является кодом некоторой булевой формулы,

(b) значение закодированной словом х булевой формулы при тех значениях фактически присутствующих в ней переменных, которые последовательно указаны в слове у, равно 1.

(Число нулей и единиц в слове у равно числу переменных, факти­чески присутствующих в закодированной булевой формуле: напри­мер, в булевой формуле x ₃V x ₁₅ фактически присутствуют две пере­менные, хотя для них и использованы большие индексы; сертифика­том выполнимости этой формулы служит, например, слово 11.) Та­кой алгоритм можно сделать полиномиальным. Это говорит о том, что при указанном способе кодирования булевых формул предикат, распознающий выполнимость булевой формулы, принадлежит клас­су NP, — сертификатом является слово у, указывающее значения пе­ременных, при которых значение булевой формулы равно 1, а зна­чение предиката R{x,у), входящего в (30.1), вычисляется с помощью алгоритма, проверяющего (a) и (b). Полином р{п) можно взять рав­ным п, так как |j| ^ |х| в силу того, что у содержит значения только тех переменных, которые фактически присутствуют в булевой фор­муле.

Неизвестно, принадлежит ли классу Р предикат на словах из Л*, распознающий выполнимость. Алгоритмы проверки выполнимости, основанные на переборе всех возможных комбинаций значений пе­ременных х_ъ х₂,..., х_п, не являются полиномиальными.

Рассмотренный пример дает мотивацию определения 30.1 и про­ясняет смысл понятия «сертификат». Отметим два важных момента.

1) Перебор всех возможных слов у, |у|^р(|х|), для проверки равенства и(х) = 1 с помощью (30.1) может потребовать рассмотре­ния экспоненциального по отношению к |х| числа возможностей. Но определение 30.1 требует лишь, чтобы при и(х) = 1 сертификат суще­ствовал, вопрос же о сложности его построения не затрагивается.

2) Если и е NP, то равенство u (x) = 0 означает, что соответству­ющего сертификата для слова у не существует. Другими словами, принадлежность х множеству истинности предиката подтверждается сертификатом, а непринадлежность —отсутствием сертификата. По-

Глава 7. Сводимость

этому возможные значения 1 и 0 не являются симметричными или равноправными; как показано в примере 30.1, предикат, распозна­ющий выполнимость булевой формулы, принадлежит NP, но мы не можем на основе только этого утверждать, что и предикат, распо­знающий невыполнимость булевой формулы, принадлежит NP (какое слово могло бы быть сертификатом невыполнимой формулы?).

Предложение 30.1. Р с NP.

Доказательство. Определим Д(х, у) = и (х) в (30.1) при любом сло­
ве у и будем считать пустое слово сертификатом любого х такого,
что и(х) = 1; в качестве полинома р берем нулевой полином. □

Продолжим рассмотрение примеров.

Пример 30.2. Согласно результатам Агравала, Кайала и Саксены (пример 22.2), классу Р принадлежит предикат, определенный на сло­вах в алфавите {0,1} и принимающий значение 1, если и только если слово является записью простого числа. Рассмотрим близкую задачу. Для заданных п, fceN⁺, к < п, выяснить, имеется ли у числа п дели­тель Z такой, что 1 < Z s= к. Числа п и к задаются в двоичной системе; используя разделитель «;», мы можем кодировать пару п, к словом в алфавите

Л₂ = {0,1,;}.

Если слово х кодирует указанным образом пару п, к, то в качестве сертификата можно взять двоичную запись некоторого конкретного делителя I, 1 < I < к. Тогда входящий в (30.1) предикат Д(х, у) должен принимать значение 1, если и только если

(a) х является кодом пары п, к, удовлетворяющей сформулирован­ным выше условиям,

(b) у является двоичной записью некоторого числа Z такого, что Z ^ к и при этом Z | к.

Существует алгоритм проверки условий (a), (b), вычислительные за­траты которого ограничены величиной С(|х| + |у|)², где С — некото­рая константа. Можно в (30.1) положить р{п) = п, так как Ык. Это говорит о том, что рассматриваемый предикат на Л* принадлежит классу NP. Неизвестно, принадлежит ли он также классу Р.

Пример 30.3. В связи с изучением классов Р и NP рассматрива­ется большое число задач на графах, при этом графы, как правило, задаются матрицами смежности. В алфавите Л₂ матрица смежности

§ 31. Существование задач распознавания, не принадлежащих Р 201

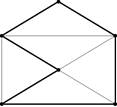
кодируется словом, в котором строки матрицы выписаны одна за дру­гой через разделитель «;». Легко видеть, что классу NP принадлежит предикат, принимающий значение 1, если и только если слово яв­ляется кодом графа, обладающего гамилътоновым циклом, т. е. цик­лом, проходящим по одному разу через все вершины графа (рис. 24);

Рис. 24. а) Гамильтонов цикл; б) граф без гамильтонова цикла.

сертификатом может, например, являться последовательность двоич­ных номеров вершин гамильтонова цикла. Эти номера выписываются в одно слово через разделитель «;».

Аналогичным образом, классу NP принадлежит предикат, прини­мающий значение 1, если и только если слово является кодом графа, обладающего кликой с заданным числом т вершин. При этом кли­кой называется набор т вершин, любые две из которых соединены ребром (в изображенном на рис. 24а графе имеется несколько клик с тремя вершинами, но нет ни одной с четырьмя вершинами). Исход­ные данные кодируются словом в алфавите Л₂: сначала идет матрица смежности, записанная так, как было сказано выше, затем, после раз­делителя «;»,—число т в двоичной системе. Эта задача принадлежит классу NP, сертификатом может быть слово, составленное из двоич­ных номеров вершин клики, перечисленных через разделитель «;».

Относительно обоих этих предикатов на Л₂ неизвестно, принад­лежат ли они классу Р.

Дата добавления: 2014-01-11