Об одном семействе алгебраических уравнений

Метод построения общего решения линейного рекуррентного уравнения с постоянными коэффициентами

Напомним метод построения общего решения линейного рекуррент­ного уравнения с постоянными коэффициентами ^г. Начнем со случая однородного уравнения

a_dy{n) + а_л__гу{п - 1) +... + а₀у(п - d) = 0. (G.1)

Пусть А_ъ А₂,..., A _s — все различные корни характеристического урав­нения

a_d A ^d + a_d _₁A ^d -¹ +...+ a ₀ = 0 (G.2)

и m₁,m₂,...,m_s — кратности этих корней, т_гт₂ +... + m_s = d. Общим решением уравнения (G.1) является

S

fc=l

где все Q_;- — произвольные постоянные.

Общее решение неоднородного линейного рекуррентного уравне­ния с постоянными коэффициентами

a_dy{n) + а_л__гу{п - 1) +... + а₀у(п - d) = /(n), (G.4)

где /(п)—известная функция, является суммой общего решения со­ответствующего однородного уравнения (G.1) и какого-нибудь част­ного решения неоднородного уравнения (G.4).

Если правая часть /(п) уравнения (G.4) представлена в виде /(") = &(") + ••• + h(n) и если известны частные решения v (n),......, w (n) для уравнений, левые части которых совпадают с левой частью уравнения (G.4), а правые части равны соответственно

См., например, [12, гл. V, § 4], [32, гл. 3].

Построение общего решения рекуррентного уравнения 239

g (n),..., h (n), то v (n) +...+ w (n) будет частным решением уравне­ния (G.4).

Если правая часть f (n) неоднородного уравнения (G.4) представ­ляет собой квазиполином, т.е. равна p(n)\хⁿ, где p(n) — полином некоторой степени l^0, а ц — некоторое (комплексное) число, то (G.4) имеет частное решение в виде квазиполинома q(n)[xⁿ, и при этом полином q(n) имеет степень l +m, где m —кратность д как кор­ня характеристического уравнения (G.2) (если д не является корнем этого уравнения, то считаем кратность нулевой: m = 0). Коэффици­енты полинома q(n) находятся методом неопределенных коэффици­ентов.

Частные решения с заданными начальными значениями находятся подстановкой в общее решение начальных значений и определением постоянных из возникшей системы линейных алгебраических урав­нений. (C помощью этого метода выводится и формула Бине (10.2).)

Приложение H

В примере 24.3 мы столкнулись с рекуррентным уравнением

y(n)-y(n-1)-...-y(n-k) = 1, (H.1)

y (0) = y (1) =... = y (k - 1) = 0. В качестве частного решения этого неоднородного уравнения при k> 1 можно взять -_k ^--. Нам предсто­ит теперь заняться общим решением соответствующего однородного уравнения, характеристическим уравнением которого служит

А ^k -А ^{k -1}-...-А-1 = 0. (H.2)

Свойства корней уравнения (H.2) описываются следующим пред­ложением.

Предложение Н.1. При k>1 уравнение (H.2) имеет k различных корней. При этом в точности один из них—мы будем называть его главным корнем уравнения (H.2) и обозначать через а_k — по модулю превосходит единицу. Главный корень — вещественное число, удовле­творяющее условию ^х 2 - - ^ а_k < 2.

Доказательство. Поскольку предстоит использовать некоторую технику теории аналитических функций, мы перейдем к привычному обозначению z для комплексной переменной и будем рассматривать уравнение z^k - z^k-¹ -... - z - 1 = 0, левую часть которого обозначим через v_k(z). Положим V_k(z) = (z- 1)v_k(z) =z^k+1 - 2z^k + 1.

Уравнение V_k(z) = 0 в сравнении с v_k(z) = 0 имеет дополнительный корень z = 1; мы докажем утверждение предложения для V_k (z) = 0,

¹ См. [28, гл. 13, пп. 7—12], [54], [20, разд. 5.4.2, упр. 7]. В [28] доказано также, что все корни, отличные от главного корня а_k, по модулю не превосходят а_k - 1 < 1.

Об одном семействе алгебраических уравнений

к > 1, откуда будет следовать требуемое. Доказательство мы проведем в три этапа, установив справедливость следующих утверждений:

(i) для любого к> 1 все корни уравнения V _fc(x) = 0 простые (т.е. имеют кратность 1);

(ii) круг любого радиуса г, 1 <г <2- -г, с центром в z = О содер­жит ровно к корней уравнения V_k(z) = 0;

(iii) уравнение V _fc(z) = 0 имеет по меньшей мере один веществен­ный корень на полуинтервале 2 - -г, 2

Для доказательства утверждения (i) заметим, прежде всего, что HOR{V_k{z),v;_c{z)) = HOR{V_k{z),z^k-¹{{k + l)z-2k)).

Но V _fc(z) не обращается в 0 при z = 0 и при z = -^. Отсюда следует, что нод04О), V _fc'(z)) = 1. Это говорит о том, что корни V_k{z) простые. Для доказательства утверждения (ii) положим W_k{z) =z^k+1 - 2z^k. Если на некоторой окружности выполняется неравенство | W_k{z) \ > 1, то внутри этой окружности полиномы V_k (z) и W_k (z) по теореме Руше ^г имеют одинаковое число корней. Рассмотрим окружность S_σ радиуса 1 + σ, 0 <σ< 1, с центром в z = 0. Так как

\W_k(z)\ = \z^k+1-2z^k\^\2z^k\-\z^k+1\,

то на окружности S_σ выполняется \W_k{z)\^ (1 + σ)^к(1 - σ). Далее, очевидно, (1 + σ)^к ^ 1 + кσ, и мы получаем, что если σ удовлетворяет неравенству

(1 + fc σ OCl - σ) > 1, (H.З)

то условия теоремы Руше выполнены, и полином V_k{z) имеет внут­ри S_σ столько же корней, сколько их имеет W_k{x), т.е. к. Нера­венство (H.З) выполнено для всех значений σ, принадлежащих ин­тервалу с концами, являющимися корнями квадратного уравнения

кσ² - (fc - 1) σ = 0, —эти корни суть 0 и 1 - р Это доказывает утвер­ждение (ii).

Наконец, утверждение (iii) следует из того, что v _fc(l) < 0, v _fc(2) > 0 и при этом уравнение v_k{z) = 0 не имеет корней на интервале

(

1,2- ^]. □

¹ См., например, [34, гл. 5, § 3] или [29, п. 1.1]. Применительно к полиномиальному случаю эта теорема допускает следующую формулировку. Пусть полином V{z) пред­ставлен в виде суммы W(z) + W(z) двух полиномов, и на контуре некоторой области значение | W (z)| меньше значения | W (z)|. Тогда внутри этой области число корней полиномов V(z) и W{z) одинаково.

Приложение H

Рекуррентное уравнение (H.1) имеет, таким образом, общее реше-

ние

у(п) = С_ка^п_к + С_к-_га^п_{к - г} +... + С_га^п_г

к-1

(а_к — главный корень характеристического уравнения (H.2), все остальные корни а_г, а₂, •••, а_к-_г по модулю не превосходят едини­цу). Нас интересует частное решение, удовлетворяющее условию у(0) = у(1) =... = у{к- 1) = 0. И без нахождения всех Q ясно, что С_кфЪ, — иначе последовательность у (к), у (к + 1),... была бы огра­ниченной.

На рис. 30 показано расположение корней уравнений V _fc(z) = 0, fc = 2,3,4.

Re z

Re z

-1

-1

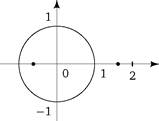
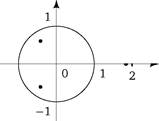Im z

Im z

а) z² - z - 1 = 0

б) z³-z²-z- 1 = 0

Re z

-1

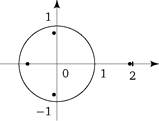Im z

в) z ⁴- z ³- z ²- z -l = 0

Рис. 30.

Итак, нам удалось обойтись без фактического нахождения корней характеристического уравнения. Более того, речь шла не об одном конкретном уравнении, а о семействе, в которое входят уравнения сколь угодно высоких степеней.

Мы получили доказательство предложения 24.1 из § 24.

Литература

[1] С.А.Абрамов. Исследование алгоритмов одновременного нахож­дения наибольшего и наименьшего элементов массива // ЖВМ и МФ. 1982. Т. 22, № 2. С. 424—428.

[2] С. А. Абрамов. Элементы анализа программ. Частичные функции на множестве состояний. М.: Наука, 1986.

[3] С. А. Абрамов, Г. Г. Гнездилова. Алгоритм управления вопросни­ком в автоматизированной обучающей системе // Вестн. Моск. ун-та. Сер. 15. Вычисл. мат. и киб. 1988. № 2. С. 47—52.

[4] В.Б.Алексеев. Введение в теорию сложности алгоритмов: Учеб­ное пособие для студентов. М.: Издательский отдел ф-та ВМиК МГУ, 2002.

[5] А.Ахо, Дж.Хопкрофт, Дж.Улъман. Построение и анализ вычис­лительных алгоритмов. М.: Мир, 1979.

[6] Н.Г.де Брейн. Асимптотические методы в анализе. М.: ИЛ, 1961.

[7] А.А.Васин, В.В.Морозов. Теория игр и модели математической экономики. Учебное пособие. М.: МАКС Пресс, 2005.

[8] Введение в криптографию / Под общей редакцией В. В. Ященко. М.: МЦНМО: ЧеРо, 2000.

[9] Н. К. Верещагин, А. Шень. Начала теории множеств. М.: МЦНМО, 2008.

[10] М.Н. Вялый. Сложность вычислительных задач // Математиче­ское просвещение, вып. 4. M.: МЦНМО, 2000. С. 81—114.

[11] С.Б.Гашков, В.Н.Чубариков. Арифметика. Алгоритмы. Слож­ность вычислений. М.: Высшая школа, 2000.

[12] А. О.Гелъфонд. Исчисление конечных разностей. М.: Наука, 1967.

Литература

[13] М.Гэри, Д.Джонсон. Вычислительные машины и труднорешае-мые задачи. М.: Мир, 1982.

[14] В.А.Ильин, Г.Д.Ким. Линейная алгебра и аналитическая геомет­рия. М.: Изд-во Моск. ун-та, 1998.

[15] А.А.Карацуба, Ю.П.Офман. Умножение многозначных чисел на автоматах // Докл. АН СССР. 1962. Т. 145, № 2. С. 293—294.

[16] А.А.Карацуба. Основы аналитической теории чисел. М.: Наука, 1975.

[17] А.А.Карацуба. Сложность вычислений // Труды Математическо­го института РАН. 1995. Т. 211. С. 186—203.

[18] Д. Кнут. Искусство программирования для ЭВМ. Т. 1. Основные алгоритмы. М.—СПб.—Киев: ИД «Вильямс», 1999.

[19] Д. Кнут. Искусство программирования для ЭВМ. Т. 2. Получис­ленные алгоритмы. М.—СПб.—Киев: ИД «Вильямс», 2000.

[20] Д. Кнут. Искусство программирования для ЭВМ. Т. 3. Сортиров­ка и поиск. М.—СПб.—Киев: ИД «Вильямс», 2001.

[21] Т. Кормен, Ч.Лейзерсон, Р.Ривест. Алгоритмы: построение и ана­лиз. М.: МЦНМО, 2000.

[22] А.И.Кострикин. Введение в алгебру. М.: Наука, 1977.

[23] В. H. Крупский. Введение в сложность вычислений. М.: Фактори­ал-Пресс, 2006.

[24] С. С. Лавров. Программирование. Математические основы, сред­ства, теория. СПб: БХВ-Петербург, 2001.

[25] В.H.Латышев. Комбинаторная теория колец: сложность алгеб­раических алгоритмов. М.: Изд-во Моск. ун-та, 1987.

[26] Дж.Макконелл. Анализ алгоритмов. Вводный курс. М.: Техно­сфера, 2002.

[27] Ф. Мостеллер. 50 занимательных вероятностных задач с реше­ниями. М.: URSS, 2005.

[28] А.М.Островский. Решение уравнений и систем уравнений. М.: ИЛ, 1963.

Литература

[29] В.В.Прасолов. Многочлены. М.: МЦНМО, 2003.

[30] Ф. Препарата, М.Шеймос. Вычислительная геометрия: введение. М.: Мир, 1989.

[31] Э.Рейнгольд, Ю.Нивергелът, Н.Део. Комбинаторные алгоритмы. Теория и практика. М.: Мир, 1980.

[32] В.К.Романко. Разностные уравнения. М.: БИНОМ. Лаборатория знаний, 2006.

[33] АА.Сапоженко. Некоторые вопросы сложности алгоритмов: учебное пособие. М.: Издательский отдел ф-та ВМиК МГУ, 2001.

[34] А. Г. Свешников, А. Н. Тихонов. Теория функций комплексной пе­ременной. М.: Физматлит, 1999.

[35] В. Серпинский. 250 задач по теории чисел. Москва—Ижевск: Ре­гулярная и хаотическая динамика, 2004.

[36] А.Л.Тоом. О сложности схемы из функциональных элементов, реализующей умножение целых чисел // Докл. АН СССР. 1963. Т. 150, № 2. С. 496—498.

[37] Дж.Хартманис, Дж.Э.Хопкрофт. Обзор теории сложности // Кибернетический сборник. 1974. Вып. 11. С. 131—176.

[38] ПЛ.Чебышев. Полное собрание сочинений. Т. 1. М.—Л.: АН СССР, 1944.

[39] И. Р. Шафаревич. Избранные главы алгебры. М.: Журнал «Мате­матическое образование», 2000.

[40] Математическая энциклопедия. Т. 1. М.: Издательство «Совет­ская энциклопедия», 1977.

[41] S.AAbramov, M.Bronstein. Hypergeometric dispersion and the orbit problem // Proceedings of the 2000 International Symposium on Symbolic and Algebraic Computation. New York: ACM, 2000. P. 8—13.

[42] M.Agrawal, N.Kayal, N.Saxena. PRIMES is in P // Ann. of Math. (2). 2004. V. 160, № 2. P. 781—793.

[43] S.Baase, A. van Gelder. Computer algorithms: introduction to design and analysis. Boston, MA: Addison-Wesley, 2000.

Литература

[44] E.Bach, J. ShaU.it. Algorithmic number theory. V. 1. Efficient algorithms. Cambridge, MA: MIT Press, 1996.

[45] P.E.Blanksby, H.L.Montgomery. Algebraic integers near the unit circle // Acta Arith. 1971. V. 18. P. 355—369.

[46] G. Brassard, P.Bratley. Fundamentals of algorithms. Englewood Cliffs, NJ: Prentice Hall, 1996.

[47] D. Coppersmith, S.Winograd. Matrix multiplication via arithmetic progressions // J. Symbolic Comput. 1990. V. 9, № 3. P. 251—280.

[48] M. J. Fischer, M. O. Rabin. Super-exponential complexity of Presburger arithmetic // Complexity of computation (Proc. SIAM-AMS Sympos., New York, 1973). Providence, RI: AMS, 1974. (SIAM-AMS Proc; Vol. VII). P. 27—41.

[49] N. Friedman. Some results on the effect of arithmetics on comparison problems // Proc. 13th IEEE Ann. Symp. on Switching and Automata Theory. Los Alamitos, CA: IEEE Computer Society, 1972. P. 139—143.

[50] J. von zur Gathen, J. Gerhard. Modern computer algebra. New York: Cambrige University Press, 1999.

[51] KKannan, KJ.Lipton. Polynomial-time algorithm for the orbit problem // J. Assoc. Comput. Mach. 1986. V. 33, № 4. P. 808—821.

[52] D.RKnuth. Big omicron and big omega and big theta // ACM SIGACT News. 1976. V. 8, iss. 2. P. 18—23.

[53] J. C. Lagarias. The 3 x + 1 problem and its generalizations // The American Mathematical Monthly. 1989. V 92, № 1. P. 3—23.

[54] E. P. Miles, Jr. Generalized Fibonacci numbers and associated ma­trices // The American Mathematical Monthly. 1960. V 67, № 8. P. 745—752.

[55] KMotwani, PRaghavan. Randomized algorithms. Cambridge: Cam­bridge University Press, 1995.

[56] I. Pohl. A sorting problem and its complexity // Comm. ACM. 1972. V. 15, № 6. P. 462—466.

Литература

[57] E. M. Reingold, A. I. Stocks. Simple proofs of lower bounds for polynomial evaluation // Complexity of computer computations (Proc. Sympos., IBM Thomas J. Watson Res. Center, Yorktown Heights, N. Y., 1972). New York: Plenum, 1972. P. 21—30.

[58] ASchinzel, H. Zassenhaus. A refinement of two theorems of Kronecker // Michigan Math. J. 1965. V. 12. P. 81—85.

[59] R. Sedgewick, P. Flajolet. An introduction to the analysis of algorithms. Boston, MA: Addison-Wesley, 1996.

Дата добавления: 2014-01-11