Построение комбинаторной логики

Комбинаторы.

Бестиповая комбинаторная логика.

Определение:

λ-выражение без свободных переменных называется комбинатором.

Позволяет избавиться от связанных переменных в λ-выражении.

Системы комбинаторов предназначены для выписывания тех же функций, что системы λ-конверсий, но без использования связанных переменных.

Пример. Ia = a

I: λx.x

Kab = a

K: λxy.x

Sabc = ac(bc)

S: λxyz.xz(yz)

Одни комбинаторы можно выражать через другие I = SKK.

Проверим это двумя способами.

1-ый способ:

Определение:

Комбинаторная характеристика – способ передачи информации об объекте в виде правил текстуального преобразования.

SKKa → Ka(Ka) → a

2-ой способ:

┌──_↓ ┌─_↓

(λxyz.xz(yz))(λxy.x)(λxy.x)→(λyz.(λxy.x)z(yz))(λxy.x)→((xy.z)(yz)→

^↑─────────└────┘

→(λyz.z)(λxy.x)→ λz.z

Определение:

Базис формальной системы - минимальный набор объектов этой системы, через который можно с помощью аксиом и правил вывода выразить все остальные объекты формальной системы.

Определение:

Базисом бестиповой комбинаторной логики является набор комбинаторов: К,S и т.д.

Определение:

Комбинаторная логика (КЛ) - часть математической логики, изучающая комбинаторы и их свойства, где функциональная абстракция выражается без использования формальных переменных.

Введем комбинаторную логику как формальную систему:

1. Алфавит: (,), х_i, с_i, S, K, I,…

комбинаторы

2. Комбинаторные термы:

- все переменные являются термами (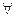х_i – терм);

- все константы являются термами (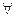с_i - терм);

- все комбинаторы являются термами (S,K,I,…- термы).

А-терм, В-терм (Если А- терм и В - терм, то аппликация (АВ)-терм)

(AB)-терм Таким образом (АВ) также является термом.

λ-абстракций в комбинаторной логике нет.

Скобки расставляются по ассоциации влево.

3. Правила вывода:

а→b _(μ) a→b _{(υ )} a→b _(τ)

ca → cb ac→bc b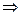→ca→c

4. Схема аксиом.

Ix → x

Kxy → x

Sxyz → xz(yz)

x → x

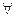x,y,z

Примеры комбинаторов. Ix = x -тождество

Bxyz = x(yz) - композитор

Wxy = xyy - дупликатор

Cxyz = xzy - пермутатор

Sxyz = xz(yz) - коннектор

Kxy = x - канцелятор

I, B, W, K - также образуют базис.

Определения:

Выражение вида Ix, Kxy, Sxyz называются редексами.

Получившиеся свернутые выражения для редексов (соответственно х, х, xz(yz)) называются контрактами либо сверткой.

Говорят, что выражение А находится в нормальной форме, если оно не содержит редексов. Для любого комбинаторного выражения существует нормальная форма.

Пример

B = S(KS)K

W = SS(K(SKK))

C = S(BBS)(KK)

Теорема Черча-Россера.

If А→В, А→С

then D:B→D, C→D

Дата добавления: 2014-01-11