Использование типов

Типизированные системы.

Преимущества комбинаторов

Базис I,B,C,S

Ой способ

a(bc) =^(K) Kac(bc) =^(S) S(Ka)bc =^(K) KSa(Ka)bc =^(S) S(KS)Kabc.

Для всей комбинаторной логики I,B,C,S не является базисом, т.к. в нем нет укорачивающего правила, которое вводится Kxy = x. Однако для систем без укорачивающих правил I,B,C,S можно использовать как базис.

K – не может быть выражено через остальные комбинаторы, значит для всей комбинаторной логики I,B,C,S - не базис.

Не содержат свободных переменных (не возникает проблемы коллизии переменных).

Убыстряются сами вычисления, которые сводятся к ряду однотипных действий.

Контрольные вопросы

1. Дайте определение комбинатора.
2. Какие свойства комбинаторов делают удобным их использование для описания аппликативных алгоритмов?
3. Дайте определение базиса формальной системы.
4. Докажите, что I, B, C, S не является базисом бестиповой комбинаторной логики.
5. Приведите определение нумералов и основных операций над ними в рамках бестиповой комбинаторной логики.
6. Выразите комбинаторы B, C, W в базисе K, S.

Типы делают систему более строгой. Если все выражения согласованы по типам, то они реализуются гораздо эффективнее.

Типы назначают вид значения, когда функция прилагается к аргументам.

Предположим, что аппликация имеет тип с, В имеет тип b, тогда А имеет тип b→c.

(АВ)^с-тип, B^b A^b→c

Если а,b – типы, то а→b тоже тип.

Пример.

Ix = x

Пусть Х^а, тогда I^a→a (т.к. должно выполняться равенство IХ^а =Х^а).

(Kx)y = x^α

x^α,y^β, то (Kx)^α→β

Kx^α = C^β→α, то К ^{α→(β→α)}

Sxyz = xz(yz)

Пусть z^α, тогда если (yz)^β, то у^α→β((хz)(уz)^β)^γ 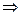(xz)^β→γ, z^α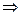x^{α→(β→γ)}

Рассмотрим (Sxyz)^γ, z^α 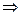(Sxy)^α→γ, известно, что у^α→β, тогда (Sx)^{(α→β)→(α→γ)}

x^{α→(β→γ)}, тогда S^{(α→(β→γ))→((α→β)→(α→γ))}

Определение:

Говорят, что тип α приписан комбинатору Х тогда и только тогда, когда это утверждение вытекает из следующих аксиом и правила вывода:

I^α→α

К^{α→(β→α)}

S ^{(α→(β→γ)) →((α→β)→(α→γ))}

X^α→β, Y^α

^{____________________}

(XY) ^β

Обозначения:

Х^α или ^├#(Х) = α,

^├# I = α→ α₁.

Пример.

1) Припишем тип аппликации (KI)

Имеем: К ^{α→(β→α)} и I^α1→α1. Тогда существует аппликация (KI)^β→α, α: α₁ → α₁.

Тогда (KI) ^{β→(α1→α1)}

2) (KI) ^{β→(α→α)}b^β→I ^γ=α→α

Дата добавления: 2014-01-11