Первый закон Ньютона. Масса. Сила

Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Законы Ньютона играют исклю­чительную роль в механике и являются (как и все физические законы) обобщени­ем результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов и опытной про­верке подвергают не каждый отдельный закон, а всю систему в целом.

Первый закон Ньютона: всякая мате­риальная точка (тело) сохраняет состоя­ние покоя или равномерного прямолиней­ного движения до тех пор, пока воздейст­вие со стороны других тел не заставит ее изменить это состояние.

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. По­этому первый закон Ньютона называют также законом инерции.

Механическое движение относительно, и его характер зависит от системы отсче­та. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами от­счета. Инерциальной системой отсчета яв­ляется такая система, которая либо по­коится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Опытным путем установлено, что инерциальной можно считать гелиоцен­трическую (звездную) систему отсчета (начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако эффекты, обусловлен­ные ее неинерциальностью (Земля враща­ется вокруг собственной оси и вокруг Со­лнца), при решении многих задач прене­брежимо малы, и в этих случаях ее можно считать инерциальной.

Из опыта известно, что при одинако­вых воздействиях различные тела неоди­наково изменяют скорость своего движе­ния, т. е., иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его мас­сы).

Масса тела — физическая величина, являющаяся одной из основных характе­ристик материи, определяющая ее инерци­онные (инертная масса) и гравитацион­ные (гравитационная масса) свойства. В настоящее время можно считать дока­занным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^-12 их значения).

Чтобы описывать воздействия, упоми­наемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т. е. приобретают ускорения (динамиче­ское проявление сил), либо деформируют­ся, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется чис­ловым значением, направлением в про­странстве и точкой приложения. Итак, сила — это векторная величина, являюща­яся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и раз­меры.

Второй закон Ньютона

Второй закон Ньютона — основной за­кон динамики поступательного движе­ния — отвечает на вопрос, как изменяет­ся механическое движение материальной точки (тела) под действием приложен­ных к ней сил.

Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всег­да прямо пропорционально равнодейст­вующей приложенных сил:

a~F (m=const). (6.1)

При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно:

а~ 1 /т (F= const). (6.2)

Используя выражения (6.1) и (6.2) и учи­тывая, что сила и ускорение — величины векторные, можем записать

a = kF/m. (6.3)

Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорцио­нально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точ­ки (тела).

В СИ коэффициент пропорциональности k = 1. Тогда

a = F /m,

или

F = m a = md v /dt (6.4)

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:

F =(d/dt)(m v). (6.5)

Векторная величина

p = m v, (6.6)

численно равная произведению массы ма­териальной точки на ее скорость и име­ющая направление скорости, называется импульсом (количеством движения) этой материальной точки.

Подставляя (6.6) в (6.5), получим

F =d p /dt (6.7)

Это выражение — более общая формули­ровка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выраже­ние (6.7) называется уравнением движе­ния материальной точки.

Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе в 1 кг сообща­ет ускорение 1 м/с² в направлении дейст­вия силы:

1 Н=1 кг•м/с².

Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае ра­венства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (6.3)) также равно нулю. Однако первый закон Ньюто­на рассматривается как самостоятельный закон (а не как следствие второго зако­на), так как именно он утверждает су­ществование инерциальных систем отсче­та, в которых только и выполняется урав­нение (6.7).

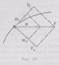
о механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одно­временно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускоре­ния можно разлагать на составляющие, использование которых приводит к су­щественному упрощению решения задач. Например, на рис. 10 действующая сила F = m a разложена на два компонента: тангенциальную силу F_t (направлена по касательной к траектории) и нормальную силу F _n (направлена по нормали к центру кривизны).

Используя выражения

а_t=dv/dt и а_n=v ² /R, а также v=Rw, можно записать:

Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под F во втором законе Ньютона понимают результирующую силу

Третий закон Ньютона

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие мате­риальных точек (тел) друг на друга носит характер взаимодействия; силы, с которы­ми действуют друг на друга материальные точки, всегда равны по модулю, противо­положно направлены и действуют вдоль прямой, соединяющей эти точки:

F ₁₂=- F _2I, (7.1)

где F ₁₂ — сила, действующая на первую материальную точку со стороны второй; F ₂₁ — сила, действующая на вторую мате­риальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

При использовании законов динамики иногда допускают следующую ошибку: так как действующая сила всегда вызыва­ет равную по модулю и противоположную по направлению силу противодействия, то, следовательно, их равнодействующая до­лжна быть равна нулю и тела вообще не могут приобрести ускорения. Однако надо помнить, что во втором законе Ньютона речь идет об ускорении, приобретаемом телом под действием приложенных к нему сил. Равенство нулю ускорения означает равенство нулю равнодействующей сил, приложенных к одному и тому же телу. Третий же закон Ньютона говорит о равен­стве сил, приложенных к различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение.

Третий закон Ньютона позволяет осу­ществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Силы трения

Обсуждая до сих пор силы, мы не интере­совались их происхождением. Однако в механике мы будем рассматривать различные силы: трения, упругости, тяготе­ния.

Из опыта известно, что всякое тело, движущееся по горизонтальной поверхно­сти другого тела, при отсутствии действия на него других сил с течением времени замедляет свое движение и в конце концов останавливается. Это можно объяснить существованием силы трения, которая

препятствует скольжению соприкасаю­щихся тел друг относительно друга. Силы трения зависят от относительных скоро­стей тел. Силы трения могут быть разной природы, но в результате их действия ме­ханическая энергия всегда превращается во внутреннюю энергию соприкасающих­ся тел.

Различают внешнее (сухое) и внутрен­нее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающих­ся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения.

Внутренним трением называется тре­ние между частями одного и того же тела, например между различными слоями жид­кости или газа, скорости которых меняют­ся от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг дру­га и разделены прослойкой вязкой жидко­сти (смазки), то трение происходит в слое смазки. В таком случае говорят о гидроди­намическом трении (слой смазки доста­точно толстый) и граничном трении (тол­щина смазочной прослойки ~0,1 мкм и меньше).

Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся повер­хностей; в случае же очень гладких по­верхностей трение обусловлено силами межмолекулярного притяжения.

Рассмотрим лежащее на плоскости те­ло (рис. 11), к которому приложена горизонтальная сила F.

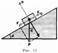
Тело придет в движе­ние лишь тогда, когда приложенная сила F будет больше силы трения F _тр. Француз­ские физики Г. Амонтон (1663—1705) и Щ. Кулон (1736—1806) опытным путем установили следующий закон: сила трения скольжения F_тр пропорциональна силе N нормального давления, с которой одно тело действует на другое:

F_тр =fN,

где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

Найдем значение коэффициента тре­ния. Если тело находится на наклонной плоскости с углом наклона а (рис. 12), то оно приходит в движение только когда тангенциальная составляющая F силы тя­жести Р больше силы трения F _тр. Следова­тельно, в предельном случае (начало скольжения тела)

F=F _тр

или

Таким образом, коэффициент трения ра­вен тангенсу угла a₀, при котором на­чинается скольжение тела по наклонной плоскости.

Для гладких поверхностей определен­ную роль начинает играть межмолекуляр­ное притяжение. Поэтому Б. В. Дерягиным (р. 1902) предложен закон трения скольжения

F _тр = f _ист (N + S_P0),

где p₀ — добавочное давление, обус­ловленное силами межмолекулярного при­тяжения, которые быстро уменьшаются с увеличением расстояния между частица­ми; S — площадь контакта между телами; f_ист — истинный коэффициент трения скольжения.

Трение играет большую роль в при­роде и технике. Благодаря трению движет­ся транспорт, удерживается забитый в стену гвоздь и т. д.

В некоторых случаях силы трения ока­зывают вредное действие, и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в 10 раз), которая заполняет неровности между этими повер­хностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно мень­шим внутренним трением жидкости.

Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники и т.д.). Сила трения качения определяется по закону Кулона:

F _тр = f _kN/r, (8.1)

где r — радиус катящегося тела; f_k — коэффициент трения качения, имеющий размерность dimf_k=L. Из (8.1) следует, что сила трения качения обратно пропорцио­нальна радиусу катящегося тела.

Закон сохранения импульса. Центр масс

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп­ность материальных точек (тел), рассмат­риваемых как единое целое, называется механической системой. Силы взаимодей­ствия между материальными точками ме­ханической системы называются внутрен­ними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют

внешние силы, называется замкнутой (или изолированной). Если мы имеем механиче­скую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направле­ны, т. е. геометрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т ₁, m ₂,..., т_n и v ₁, v ₂,..., v _n. Пусть F '₁, F '₂,..., F '_n — равнодействующие внутренних сил, действующих на каждое из этих тел, a f ₁, f ₂,..., F _n — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:

d/dt(m₁v₁)= F '₁+ F ₁,

d/dt(m₂v₂)= F' ₂+ F ₂,

d/dt)mn v _n)= F '_n+ F _n.

Складывая почленно эти уравнения, получим

d/dt (m₁ v ₁+m₂ v ₂+... + m_n v _n) = F '₁+ F '₂+...+ F ' _n + F ₁+ F ₂+...+ F _n.

Но так как геометрическая сумма внутрен­них сил механической системы по третьему закону Ньютона равна нулю, то

d/dt(m₁v₁+m₂v₂ +... + m_nv_n)= F ₁ + F ₂+...+ F _n, или

dp/dt= F ₁+ F ₂+...+ F _n, (9.1)

где

импульс системы. Таким образом, производная по времени от им­пульса механической системы равна гео­метрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

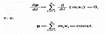
Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса справед­лив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон со­хранения импульса — фундаментальный закон природы.

Закон сохранения импульса является следствием определенного свойства сим­метрии пространства — его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

Отметим, что согласно (9.1), импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю.

В механике Галилея — Ньютона из-за независимости массы от скорости импульс системы может быть выражен через ско­рость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распре­деление массы этой системы. Ее радиус-вектор равен

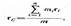
где m_i и r_i — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе;

— масса системы.

Скорость центра масс

Учитывая, что p _i =m_i v _i, а

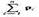
есть импульс р системы, можно написать

p = m v _c, (9.2)

т. е. импульс системы равен произведе­нию массы системы на скорость ее цент­ра масс.

Подставив выражение (9.2) в уравне­ние (9.1), получим

mdv_c/dt= F ₁+ F ₂+...+ F _n, (9.3)

т. е. центр масс системы движется как материальная точка, в которой сосредото­чена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Выражение (9.3) представляет собой закон движения центра масс.

В соответствии с (9.2) из закона со­хранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остает­ся неподвижным.

Уравнение движения тела переменной массы

Движение некоторых тел сопровождается изменением их массы, например масса ра­кеты уменьшается за счет истечения газов, образующихся при сгорании топлива, и т. п.

Выведем уравнение движения тела пе­ременной массы на примере движения ра­кеты. Если в момент времени t масса раке­ты т, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm

и станет равной т- dm, а скорость станет равной v +d v. Изменение импульса систе­мы за отрезок времени dt

dp = [(m-dm) (v +d v)+dm (v + u)]- m v,

где и — скорость истечения газов относи­тельно ракеты. Тогда

d p = md v + u dm

(учли, что dm dv — малый высшего порядка малости по сравнению с осталь­ными).

Если на систему действуют внешние силы, то d p = F dt, поэтому

F dt = md v + u dm,

md v /dt= F - u dm/dt. (10.1)

Член - u dm/dt называют реактивной силой

at

F _p. Если u противоположен v, то ракета ускоряется, а если совпадает с v, то тормо­зится.

Таким образом, мы получили уравне­ние движения тела переменной массы

m a = F + F _p, (10.2)

которое впервые было выведено И. В.Ме­щерским (1859—1935).

Идея применения реактивной силы для создания летательных аппаратов высказы­валась в 1881 г. Н. И. Кибальчичем (1854—1881). К.Э.Циолковский (1857— 1935) в 1903 г. опубликовал статью, где

предложил теорию движения ракеты и ос­новы теории жидкостного реактивного двигателя. Поэтому его считают основате­лем отечественной космонавтики.

Применим уравнение (10.1) к движе­нию ракеты, на которую не действуют ни­какие внешние силы. Полагая F = 0 и счи­тая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим

dv dm т dv/dt=-udm/dt. откуда

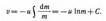
Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ра­кеты равна нулю, а ее стартовая масса то, то С = uln m₀. Следовательно,

v = uln(m₀/m). (10.3)

Это соотношение называется формулой Циолковского. Она показывает, что: 1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты то; 2) чем больше скорость истече­ния и газов, тем больше может быть ко­нечная масса при данной стартовой массе ракеты.

Выражения (10.2) и (10.3) получены для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью света с.

Работа и энергия

§11. Энергия, работа, мощность

Энергия — универсальная мера различ­ных форм движения и взаимодействия. С различными формами движения мате­рии связывают различные формы энергии: механическую, тепловую, электромагнит­ную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холод­ное), в других — переходит в иную фор­му (например, в результате трения меха­ническое движение превращается в тепло­вое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы

количественно характеризовать процесс обмена энергией между взаимодействую­щими телами, в механике вводится по­нятие работы силы.

Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с на­правлением перемещения, то работа этой силы равна произведению проекции силы F_s на направление перемещения (F_s = Fcosa), умноженной на перемещение точки приложения силы:

A = F_ss = F_s cosa. (11.1)

В общем случае сила может изменять­ся как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться не­льзя. Если, однако, рассмотреть элемен­тарное перемещение dr, то силу F можно считать постоянной, а движение точки ее

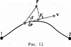
приложения — прямолинейным. Элемен­тарной работой силы F на перемещении d r называется скалярная величина

dА = F d r = Fcos a• ds=F_sds,

где а — угол между векторами F и d r; ds = |d r | — элементарный путь; F_s — про­екция вектора F на вектор d r (рис. 13).

Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сум­ма приводится к интегралу

Для вычисления этого интеграла надо знать зависимость силы F_s от пути s вдоль траектории 1 — 2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графи­ке площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F=const и a=const, то получим

где s — пройденный телом путь (см. также формулу (11.1)).

Из формулы (11.1) следует, что при a<p/2 работа силы положительна, в этом случае составляющая F _s совпадает

по направлению с вектором скорости дви­жения v (см. рис. 13). Если a>p/2, то работа силы отрицательна. При a = p/2 (сила направлена перпендикулярно пере­мещению) работа силы равна нулю.

Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н•м).

Чтобы охарактеризовать скорость со­вершения работы, вводят понятие мощ­ности:

N=da/dt. (11.3)

За время dt сила F совершает работу F d r, и мощность, развиваемая этой силой, в данный момент времени

N= F d r /dt= Fv

т. е. равна скалярному произведению век­тора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.

Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).

Кинетическая и потенциальная энергии

Кинетическая энергия механической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает рабо­ту, а энергия движущегося тела возраста­ет на величину затраченной работы. Таким образом, работа dA силы F на пути, кото­рый тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.

dA= dT.

Используя второй закон Ньютона F =md v /dt

и умножая обе части равен­ства на перемещение d r, получим

F d r =m(d v /dt)dr=dA

Таким образом, тело массой т, движущее­ся со скоростью v, обладает кинетической энергией

Т = тv²/2. (12.1)

Из формулы (12.1) видно, что кинети­ческая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее дви­жения.

При выводе формулы (12.1) предпола­галось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать за­коны Ньютона. В разных инерциальных системах отсчета, движущихся друг отно­сительно друга, скорость тела, а следова­тельно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетиче­ская энергия зависит от выбора системы отсчета.

Потенциальная энергия — механиче­ская энергия системы тел, определяемая их взаимным расположением и характе­ром сил взаимодействия между ними.

Пусть взаимодействие тел осуществля­ется посредством силовых полей (напри­мер, поля упругих сил, поля гравитацион­ных сил), характеризующихся тем, что работа, совершаемая действующими сила­ми при перемещении тела из одного поло­жения в другое, не зависит от того, по какой траектории это перемещение прои­зошло, а зависит только от начального и конечного положений. Такие поля на­зываются потенциальными, а силы, дей­ствующие в них,— консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является си­ла трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией II. Работа консервативных сил при элемен­тарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

dA=-dП. (12.2)

Работа d А выражается как скалярное произведение силы F на перемещение d r и выражение (12.2) можно записать в виде

F d r =-dП. (12.3)

Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению.

Потенциальная энергия может быть определена исходя из (12.3) как

где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной по­стоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциаль­ную энергию тела в каком-то определен­ном положении считают равной нулю (вы­бирают нулевой уровень отсчета), а энер­гию тела в других положениях отсчитыва­ют относительно нулевого уровня. Для консервативных сил

или в векторном виде

F =-gradП, (12.4) где

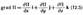
(i, j, k — единичные векторы координат­ных осей). Вектор, определяемый выраже­нием (12.5), называется градиентом ска­ляра П.

Для него наряду с обозначением grad П применяется также обозначение ÑП. Ñ («набла») означает символический вектор, называе­мый оператором Гамильтона или набла-оператором:

Конкретный вид функции П зависит от характера силового поля. Например, по­тенциальная энергия тела массой т, под­нятого на высоту h над поверхностью Зем­ли, равна

П = mgh, (12.7)

где высота h отсчитывается от нулевого уровня, для которого П₀ = 0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.

Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (ки­нетическая энергия всегда положитель­на!}. Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h'), П =-mgh'.

Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна дефор­мации:

F_{х упр=} -kx,

где F_xупр — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус ука­зывает, что F_{x упр} направлена в сторону, противоположную деформации х.

По третьему закону Ньютона, дефор­мирующая сила равна по модулю силе упругости и противоположно ей направле­на, т. е.

F_x=-F_{x упр=kx} Элементарная работа dA, совершаемая силой F_x при бесконечно малой деформации dx, равна

dA = F_x dx = kxdx,

а полная работа

идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела

П =kx²/2.

Потенциальная энергия системы, подо­бно кинетической энергии, является функ­цией состояния системы. Она зависит толь­ко от конфигурации системы и ее положе­ния по отношению к внешним телам.

Полная механическая энергия систе­мы — энергия механического движения и взаимодействия:

Е = Е+П,

т. е. равна сумме кинетической и потен­циальной энергий.

Закон сохранения энергии

Закон сохранения энергии — результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М. В. Ломоносову (1711 —1765), изложив­шему закон сохранения материи и движе­ния, а количественная формулировка за­кона сохранения энергии дана немецким врачом Ю. Майером (1814—1878) и не­мецким естествоиспытателем Г. Гельмгольцем (1821 — 1894).

Рассмотрим систему материальных то­чек массами m₁, m ₂ ,..., m_n, движущихся со скоростями v ₁, v ₂,..., v _n. Пусть F '₁, F '₂,..., F ' _n — равнодействующие внутренних кон­сервативных сил, действующих на каждую из этих точек, a f ₁, F ₂,..., F _n— равнодей­ствующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние некон­сервативные силы; равнодействующие этих сил, действующих на каждую из ма­териальных точек, обозначим f ₁, f ₂,..., f_n. При v<<с массы материальных точек

постоянны и уравнения второго закона Ньютона для этих точек следующие:

Двигаясь под действием сил, точки системы за интервал времени dt соверша­ют перемещения, соответственно равные d r ₁, d r ₂,..., d r _n. Умножим каждое из урав­нений скалярно на соответствующее перемещение и, учитывая, что dr_i = v_idt, получим:

Сложив эти уравнения, получим

Первый член левой части равенства (13.1)

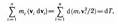
где dT есть приращение кинетической энергии системы. Второй член

равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dП системы (см. (12.2)).

Правая часть равенства (13.1) задает работу внешних неконсервативных сил,

действующих на систему. Таким образом, имеем

d(T+ П )=dA. (13.2)

При переходе системы из состояния 1 в ка­кое-либо состояние 2

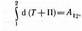
т. е. изменение полной механической энер­гии системы при переходе из одного со­стояния в другое равно работе, совершен­ной при этом внешними неконсервативны­ми силами. Если внешние неконсерватив­ные силы отсутствуют, то из (13.2) следует, что

d(Т+П) = 0,

откуда

Т+П = E=const, (13.3)

т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохране­ния механической энергии: в системе тел, между которыми действуют только кон­сервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.

Механические системы, на тела кото­рых действуют только консервативные си­лы (внутренние и внешние), называются консервативными системами. Закон сохра­нения механической энергии можно сфор­мулировать так: в консервативных систе­мах полная механическая энергия сохра­няется.

Закон сохранения механической энер­гии связан с однородностью времени, т. е. инвариантностью физических зако­нов относительно выбора начала отсчета времени. Например, при свободном паде­нии тела в поле сил тяжести его скорость и пройденный путь зависят лишь от на­чальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.

Существует еще один вид систем — диссипативные системы, в которых меха­ническая энергия постепенно уменьшается за счет преобразования в другие (немеха-нические) формы энергии. Этот процесс получил название диссипации (или рассе­яния) энергии. Строго говоря, все системы в природе являются диссипативными.

В консервативных системах полная механическая энергия остается постоян­ной. Могут происходить лишь превраще­ния кинетической энергии в потенциаль­ную и обратно в эквивалентных количе­ствах, так что полная энергия остается неизменной. Поэтому, как указывает Ф. Энгельс, этот закон не есть просто за­кон количественного сохранения энергии, а закон сохранения и превращения энер­гии, выражающий и качественную сторо­ну взаимного превращения различных форм движения друг в друга. Закон со­хранения и превращения энергии — фун­даментальный закон природы, он справед­лив как для систем макроскопических тел, так и для систем микротел.

В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механи­ческой энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количест­во энергии другого вида. Таким образом, энергия никогда не исчезает и не появля­ется вновь, она лишь превращается из одного вида в другой. В этом и заключает­ся физическая сущность закона сохране­ния и превращения энергии — сущность неуничтожимости материи и ее движения.

Удар абсолютно упругих и неупругих тел

Примером применения законов сохране­ния импульса и энергии при решении ре­альной физической задачи является удар абсолютно упругих и неупругих тел.

Удар (или соударение) — это столкно­вение двух или более тел, при котором взаимодействие длится очень короткое время. Исходя из данного определения, кроме явлений, которые можно отнести к ударам в прямом смысле этого слова(столкновения атомов или биллиардных шаров), сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т. д. При ударе в телах воз­никают столь значительные внутренние силы, что внешними силами, действующи­ми на них, можно пренебречь. Это по­зволяет рассматривать соударяющиеся те­ла как замкнутую систему и применять к ней законы сохранения.

Тела во время удара претерпевают деформацию. Сущность удара заключает­ся в том, что кинетическая энергия относи­тельного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара име­ет место перераспределение энергии меж­ду соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего пре­жнего значения. Это объясняется тем, что нет идеально упругих тел и идеально глад­ких поверхностей. Отношение нормальных составляющих относительной скорости тел после и до удара называется коэффици­ентом восстановления e:

e = v'_n/v_n.

Если для сталкивающихся тел e=0, то такие тела называются абсолютно неупру­гими, если e=1 —абсолютно упругими.

На практике для всех тел 0<e<1 (например, для стальных шаров e»0,56, для шаров из слоновой кости e»0,89, для свинца e»0). Однако в не­которых случаях тела можно с большой точностью рассматривать либо как абсо­лютно упругие, либо как абсолютно не­упругие.

Прямая, проходящая через точку со­прикосновения тел и нормальная к повер­хности их соприкосновения, называется линией удара. Удар называется централь­ным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсо­лютно неупругие удары.

Абсолютно упругий удар — столкнове­ние двух тел, в результате которого в обо­их взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинети­ческую энергию

.

Для абсолютно упругого удара вы­полняются закон сохранения импульса и закон сохранения кинетической энергии.

Обозначим скорости шаров массами m ₁ и m ₂ до удара через v₁ и v₂, после удара — через v'₁ и v'₂ (рис. 18). При пря­мом центральном ударе векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припи­шем движению вправо, отрицательное — движению влево.

При указанных допущениях законы сохранения имеют вид

Произведя соответствующие преобра­зования в выражениях (15.1) и (15.2), по­лучим

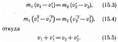
Решая уравнения (15.3) и (15.5), находим

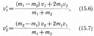
Разберем несколько примеров.

Проанализируем выражения (15.8) и (15.9) для двух шаров различных масс:

а) m ₁ =m ₂. Если второй шар до удара висел неподвижно (v ₂=0) (рис. 19), то после удара остановится первый шар (v'₁=0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (v' ₂ = v ₁ );

б) m ₁> m ₂.

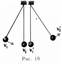
Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (v' ₁ <v ₁ ). Скорость второго шара после удара боль­ше, чем скорость первого после удара (v'₂>v'₁) (рис.20);

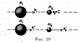
в) m ₁< m₂. Направление движения первого шара при ударе изменяется — шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т.е. v' ₂ <v ₁ (рис. 21);

г) m ₂>> m ₁ (например, столкновение шара со стеной). Из уравнений (15.8) и (15.9) следует, что v' ₁ =-v ₁, v' ₂ »2 m₁v₁/m₂ » 0.

2) При m ₁= m 2 выражения (15.6) и (15.7) будут иметь вид

v' ₁ =v ₂, v' ₂ =v ₁,

т. е. шары равной массы «обмениваются» скоростями.

Абсолютно неупругий удар — столкно­вение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.

Продемонстрировать абсолют­но неупругий удар можно с помощью ша­ров из пластилина (глины), движущихся навстречу друг другу (рис. 22).

Если массы шаров m₁ и m₂, их скоро­сти до удара v₁ и v₂, то, используя закон сохранения импульса, можно записать

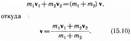
Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигал­ся шар, обладающий большим импульсом. В частном случае если массы шаров равны (m ₁ =m ₂ ), то

v = (v₁+v₂)/2.

Выясним, как изменяется кинетиче­ская энергия шаров при центральном аб­солютно неупругом ударе. Так как в процессе соударения шаров между ними дей-ствуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механи­ческой энергии не должен соблюдаться. Вследствие деформации происходит «по­теря» кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту «потерю» можно определить по раз­ности кинетической энергии тел до и после удара:

Если ударяемое тело было первона­чально неподвижно (v ₂ = 0), то

Когда m ₂ >>m ₁ (масса неподвижного тела очень большая), то v<<v ₁ и почти вся кинетическая энергия тела при ударе пере­ходит в другие формы энергии. Поэтому, например, для получения значительной де­формации наковальня должна быть мас­сивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей (m ₁ >>m ₂ ), тогда v»v ₁ и практически вся энергия затрачи­вается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.

Абсолютно неупругий удар — пример того, как происходит «потеря» механиче­ской энергии под действием диссипативных сил.

Механика твердого тела

§ 16. Момент инерции

При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) отно­сительно оси вращения называется физи­ческая величина, равная сумме произведе­ний масс n материальных точек системы на квадраты их расстояний до рассматри­ваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу

где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с коорди­натами х, у, z.

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой Л и радиусом R относительно его геометрической оси (рис.23). Разобьем

цилиндр на отдельные полые концентриче­ские цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним — r+dr. Момент инерции каждого полого цилиндра dJ = r²dm (так как dr<<r, то считаем, что расстояние всех точек ци­линдра от оси равно r), где dm — масса всего элементарного цилиндра; его объем 2prhdr. Если r — плотность материала, то dm= r• 2prhdr и dJ = 2prr³dr. Тогда мо­мент инерции сплошного цилиндра

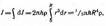
но так как p R'²h — объем цилиндра, то его масса m = pR²hr, а момент инерции

J = 1/2R².

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относи­тельно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, про­ходящей через центр масс С тела, сло­женному с произведением массы m тела на квадрат расстояния а между осями: J = J_c + ma². (16.1)

Таблица 1

В заключение приведем значения мо­ментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).

Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвиж­ной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными мас­сами m ₁, m ₂ ,..., m_n, находящиеся на рас­стоянии r ₁, r ₂,..., r_n от оси вращения. При вращении твердого тела относительно не­подвижной оси отдельные его элементар­ные объемы массами m_i, опишут окружно­сти различных радиусов r_i и имеют раз­личные линейные скорости v_i. Но так как мы рассматриваем абсолютно твердое те­ло, то угловая скорость вращения этих объемов одинакова:

w = v ₁ /r ₁ = v ₂ /r ₂ =... = v_n/r_n. (17.1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

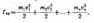
или

Используя выражение (17.1), получим

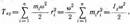
где J_z — момент инерции тела относитель­но оси 2. Таким образом, кинетическая энергия вращающегося тела

T_вр = J_zw²/2. (17.2)

Из сравнения формулы (17.2) с вы­ражением (12.1) для кинетической энер­гии тела, движущегося поступательно (T= mv²/2), следует, что момент инерции вращательного движения — мера инер­тности тела. Формула (17.2) справедлива для тела, вращающегося вокруг непод­вижной оси.

В случае плоского движения тела, на­пример цилиндра, скатывающегося с на­клонной плоскости без скольжения, энер­гия движения складывается из энергии поступательного движения и энергии вра­щения:

где m — масса катящегося тела; v_c — ско­рость центра масс тела; J _с — момент инерции тела относительно оси, проходя­щей через его центр масс; w — угловая скорость тела.

Момент силы. Уравнение динамики вращательного движения твердого тела

Моментом силы F относительно неподвиж­ной точки О называется физическая вели­чина, определяемая векторным произведе­нием радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):

M = [ rF ].

Здесь М — псевдовектор, его направление совпадает с направлением поступательно­го движения правого винта при его враще­нии от г к F.

Модуль момента силы

M = Frsina= Fl, (18.1)

где a — угол между г и F; rsina = l — кратчайшее расстояние между линией дей­ствия силы и точкой О — плечо силы.

Моментом силы относительно непод­вижной оси z называется скалярная вели­чина М_z, равная проекции на эту ось век­тор а М момента силы, определенного от­носительно произвольной точки О данной оси 2 (рис.26). Значение момента М_z не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора М, то момент силы представля-

ется в виде вектора, совпадающего с осью:

М _z = [ rF ]_z.

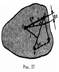
Найдем выражение для работы при вращении тела (рис.27). Пусть сила F приложена в точке В, находящейся от оси вращения на расстоянии r, a — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твер­дое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dj точка приложения В проходит путь ds= rdj, и работа равна произведению проекции силы на направление смещения на величину смещения:

dA=F sinardj. (18.2) Учитывая (18.1), можем записать dA=M_zdj,

где Fr sina = Fl =M_z — момент силы от­носительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол пово­рота.

Работа при вращении тела идет на увеличение его кинетической энергии:

dA = dT, но

Учитывая, что w=dj/dt, получим

Уравнение (18.3) представляет собой уравнение динамики вращательного дви­жения твердого тела относительно непод­вижной оси.

Можно показать, что если ось враще­ния совпадает с главной осью инерции (см. §20), проходящей через центр масс, то имеет место векторное равенство

где J — главный момент инерции тела (момент инерции относительно главной оси).

Момент импульса и закон его сохранения

При сравнении законов вращательного и поступательного движений просматрива­ется аналогия между ними, только во вра­щательном движении вместо силы «вы­ступает» ее момент, роль массы играет момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.

Моментом импульса (количества дви­жения) материальной точки А относитель­но неподвижной точки О называется физи­ческая величина, определяемая векторным произведением:

L = [ rp | = [ r m v ],

где r — радиус-вектор, проведенный из точки О в точку A; p = m v — импульс ма­териальной точки (рис.28); L —псевдо­вектор, его направление совпадает с на­правлением поступательного движения правого винта при его вращении от r к p. Модуль вектора момента импульса

L = rp sinalfa =mvr sinalfa= pl,

где a — угол между векторами r и p, l — плечо вектора р относительно точки О.

Моментом импульса относительно не­подвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О дан­ной оси. Значение момента импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого те­ла вокруг неподвижной оси z каждая от­дельная точка тела движется по окружно­сти постоянного радиуса r_i с некоторой

скоростью v_i. скорость v_i; и импульс m _iv_i

перпендикулярны этому радиусу, т. е. ра­диус является плечом вектора m_i v _i. Поэто­му можем записать, что момент импульса отдельной частицы

L_iz = т_iv_ir_i (19.1)

и направлен по оси в сторону, определяе­мую правилом правого винта.

Момент импульса твердого тела отно­сительно оси есть сумма моментов импуль­са отдельных частиц:

Используя формулу (17.1) v_i = wr_i, получим

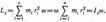
т. е.

L_z = J_zw. (19.2)

Таким образом, момент импульса твердого тела относительно оси равен произведе­нию момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем уравнение (19.2) по времени:

т. е.

dL_z/dt= M_z

Это выражение — еще одна форма урав­нения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место век­торное равенство

d L /dt= М. (19.3)

В замкнутой системе момент внешних сил М =0 и d L /dt=0, откуда

L = const. (19.4)

Выражение (19.4) представляет собой закон сохранения момента импульса: мо­мент импульса замкнутой системы сохра­няется, т. е. не изменяется с течением времени.

Закон сохранения момента импуль­са — фундаментальный закон природы, Он связан со свойством симметрии про­странства — его изотропностью, т. е. с ин-

вариантностью физических законов отно­сительно выбора направления осей коор­динат системы отсчета (относительно поворота замкнутой системы в простран­стве на любой угол).

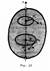
Продемонстрировать закон сохране­ния момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидя­щий на скамье, которая без трения враща­ется вокруг вертикальной оси, и держа­щий в вытянутых руках гантели (рис. 29), приведен во вращение с угловой скоро­стью w₁. Если человек прижмет гантели к себе, то момент инерции системы умень­шится. Поскольку момент внешних сил равен нулю, момент импульса системы со­храняется и угловая скорость вращения w₂ возрастает. Аналогично, гимнаст во время прыжка через голову поджимает к тулови­щу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.

Сопоставим основные величины и уравнения, определяющие вращение те­ла вокруг неподвижной оси и его поступа­тельное движение (табл.2).

Свободные оси. Гироскоп

Для того чтобы сохранить положение оси вращения твердого тела с течением време­ни неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, кото­рые не изменяют своей ориентации в про­странстве без действия на нее внешних сил. Эти оси называются свободными ося­ми (или осями свободного вращения). Можно доказать, что в любом теле су­ществуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллеле­пипеда проходят через центры противопо­ложных граней (рис. 30). Для однородно­го цилиндра одной из главных осей инер­ции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоско­сти, перпендикулярной геометрической оси цилиндра. Главными осями инерции шара

являются любые три взаимно перпендику­лярные оси, проходящие через центр масс.

Для устойчивости вращения большое значение имеет, какая именно из свобод­ных осей служит осью вращения.

Можно показать, что вращение во­круг главных осей с наибольшим и наи­меньшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым. Так, если подбросить тело, имеющее форму параллелепипеда, приведя его одновре­менно во вращение, то оно, падая, будет устойчиво вращаться вокруг осей <

Дата добавления: 2014-01-11