Тонкая линза. Формула линзы

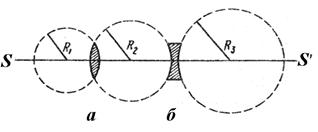Линзой называется прозрачное тело, ограниченное двумя криволинейными поверхностями. На рис. 3.5 изображены поперечные сечения двояковыпуклой а и двояковогнутой б сферических линз. Прямая SS ^', проходящая через центры кривизны

Рис. 3.5

поверхностей, образующих линзу, называется главной оптической осью линзы. Рассмотрим только тонкие линзы, толщина О ₁ О ₂которых пренебрежительно мала по сравнению с радиусами кривизны линзы (рис. 3.6).

Рис. 3.6

Рис. 15. 6

У тонкой линзы имеется точка О, обладающая тем свойством, что проходящие через нее лучи практически не преломляются линзой. Эту точку называют оптическим центром линзы; она лежит на пересечении главной оптической оси со средним сечением NN^' линзы. Любая прямая РР^', проходящая под углом к главной оптической оси через оптический центр линзы, называется побочной осью.

Рис. 15. 6

Линзу можно представить как совокупность множества призм (рис. 3.7). Тогда становится очевидным, что выпуклая линза отклоняет лучи к оптической оси, а вогнутая – от оптической оси, поэтому выпуклая линза называется собирающей, а вогнутая – рассеивающей.

Рис. 3.7

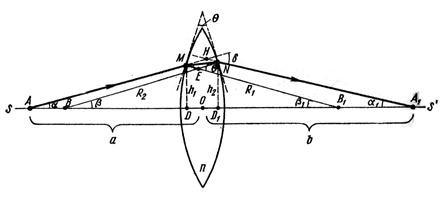
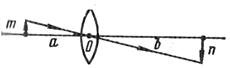
Покажем, что лучи, исходящие из некоторой точки А, лежащей на оптической оси, под небольшим углом αк этой оси, собираются линзой в одну точку А ₁, расположенную также на оптической оси и называемую изображением точки А (рис. 3.8).

		Рис. 3.8
	Рис. 3.8

Проведем плоскости, касательные к поверхностям линзы в точках М и N, и проведем в эти точки радиусы кривизны R ₁и R ₂линзы. Тогда луч AMNA можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом Ө. Учитывая малость углов α, β, α₁, β ₁и толщины линзы, можно записать следующие приближенные равенства:

h ₁≈ h ₂, АD ≈ a, A ₁ D ₁ ≈ b, α ≈ tg α ≈ h ₁/ a,

(3.5)

α₁ ≈ tg α₁ ≈ h ₁/ b, β ≈ sin β ≈ h ₁/ R ₂, β ₁≈ sin β ₁= h ₁/ R ₁.

Из треугольников AHA ₁и BEB ₁следует, что

δ = α + α₁ и Ө = β + β ₁.

Принимая во внимание формулы (3.5), получим

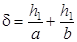и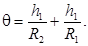

Но, согласно формуле (3.4), δ = (n – 1)Ө. Поэтому

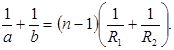(3.6)

Полученное соотношение называется формулой линзы. В формулу не входит высота h ₁. Это означает, что расстояние b не зависит от местоположения точки М, т.е. все лучи, исходящие из точки А, соберутся после преломления различными частями линзы в одной точке А ₁.

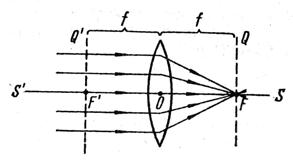Если точка А находится бесконечно далеко от линзы (а = ∞),т.е. лучи падают на линзу параллельно главной оптической оси (рис. 3.9), то, согласно формулы (3.6)

Рис. 3.9

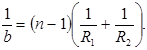
Соответствующее этому случаю расстояние b = OF = f называется фокусным расстоянием линзы:

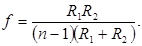(3.7)

При данной окружающей среде f зависит только от показателей преломления и радиусов кривизны линзы. Точки F и F ', лежащие по обе стороны линзы на расстоянии, равном фокусному, называют фокусами линзы. Плоскости, проходящие через фокусы перпендикулярно главной оптической оси, называются фокальными плоскостями линзы.

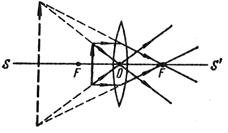
Можно показать, что лучи, падающие на линзу параллельно побочной оптической оси, сходятся после преломления в точке N, лежащей в фокальной плоскости (рис. 3.10).

	Рис. 3.10

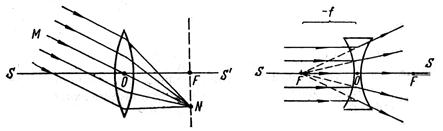
Принимая во внимание формулу (3.7), можно записать формулу линзы (3.6) в виде

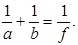(3.8)

Величина, обратная фокусному расстоянию, называется оптической силой линзы:

D = 1/ f.

Оптическая сила выражается в диоптриях (дп).

Рис. 3.11

Линейный размер изображения nопределяется по линейному размеру mиз очевидного соотношения (рис. 3.11)

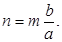
Отношение

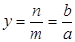(3.9)

называется линейным увеличением.

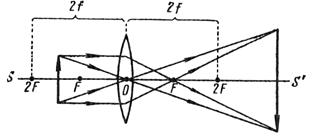
Изображение, даваемое линзой, можно получить, используя геометрическое построение. Для этого достаточно провести от каждой из крайних точек предмета по два луча. Один луч должен быть параллельным оптической оси (проходящим через фокус после преломления в линзе), другой – центральным (не преломляется линзой). Пересечение двух таких лучей дает изображение крайней точки предмета. Примеры построения изображений приведены на рис. 3.12.

	Рис. 3.12

Дата добавления: 2014-01-11