Опыты Штерна и Герлаха. Спин электрона

Орбитальный момент импульса и магнитный момент электрона в классической и квантовой механике

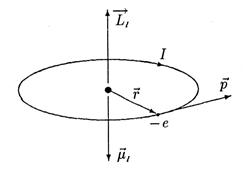Представим себе, что электрон в атоме движется со скоростью v по орбите радиуса r (рис. 10.3). Как любая движущая частица, электрон обладает моментом импульса 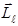, который равен произведению момента инерции на угловую скорость:

.

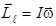Вектор 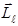перпендикулярен плоскости, в которой лежит орбита электрона, а его модуль

Рис. 10.3

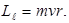
Движущийся по орбите электрон создает электрический ток, сила которого

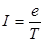, где - период обращения электрона вокруг ядра.

Электрический ток, текущий в замкнутом контуре, характеризуется магнитным моментом 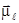. Направление вектора 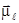связано с направлением тока правилом правого винта (рис. 10.3). Модуль магнитного момента равен произведению силы тока на площадь контура S:

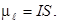Так как S = πr ², получаем .

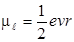Отношение магнитного момента 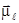частицы к ее механическому моменту 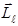, т. е. к ее моменту импульса, называют гиромагнитным отношением. Для электрона на орбите это отношение равно

.

Так как векторы 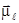и 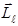антипараллельны, справедливо равенство

.

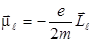В квантовой механике (из-за наличия волновых свойств) модуль орбитального момента импульса принимает дискретные значения. Используя уравнение Щредингера можно показать, что

,

где l – орбитальное квантовое число, которое может принимать следующие значения:

l = 0, 1, 2, …, n – 1.

Проекция этой физической величины на направление поля в пространстве определяется формулой:

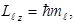
где магнитное квантовое число m_l принимает значения:

m_l = 0, ±1, ±2 …, ± l.

Равенство 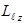и 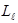запрещено соотношениями неопределенностей. Действительно, если бы выполнилось равенство отмеченных величин, произведение неопределенностей координаты и импульса в направлении поля (оси z) было бы равно 0.

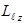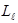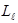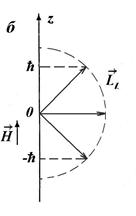
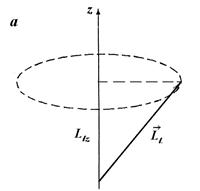
В квантовой механике определенные значения имеют и . Проекции на другие направления остаются неопределенными. Учитывая сказанное, вектор орбитального момента импульса 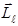можно представить как вектор, который равномерно вращается вокруг оси z, образуя с этой осью угол θ (рис. 10.4 а), определяемый соотношением

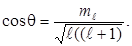
П ри заданном значении l m_l может принимать (2 l + 1) значение.

	Рис. 10.4

Например, при l = 1, , а L_lz =0, ± 1 (рис. 10.4б).

Магнитный момент электрона, обусловленный орбитальным движением, 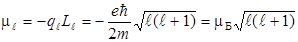, а его проекция на направление поля 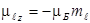, где 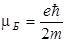- магнетон Бора.

Рис. 10.5

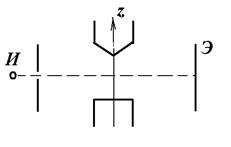По законам квантовой механики орбитальные моменты импульса и магнитные моменты и их проекции, на направление магнитного поля, у электронов в атоме должны принимать дискретные значения. В справедливости данного факта необходимо было убедиться, так как он противоречил законам классической физики. Непосредственно измерить момент импульса электрона в атоме невозможно. Однако можно измерить проекцию магнитного момента атома на направление внешнего магнитного поля. Такие измерения осуществили Штерн и Герлах в 1922 г. Принципиальная схема их установки приведена на рис. 10.5. И – источник атомов (вещество нагревалось до высокой температуры, при которой наблюдалось интенсивное испарение атомов). Поток атомов пролетал через неоднородное магнитное поле. На атомы в этом поле должна действовать сила

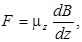
где 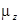- проекция магнитного момента атома на направление поля, а 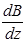- градиент магнитной индукции. Если бы 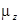могло принимать любые значения, то распределение интенсивности попадания частиц на экране было бы таким, как приведено на рис. 10.6 а, при дискретных значениях 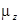должно наблюдаться распределение рис. 10.6 б. Эксперименты показали, что поток атомов в неоднородном поле разбивается на несколько дискретных пучков. Но был обнаружен и неожиданный результат: если использовать атомы первой группы таблицы Менделеева (Cu, Ag, Au), магнитное поле

разбивает поток этих атомов на 2 потока (рис. 10.6 в). Эти элементы не должны были отклонятся магнитным полем. При проведении эксперимента считали, что магнитный момент атома равен суммарному магнитному моменту валентных электронов (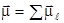). У элементов 1 группы один валентный электрон, который находится в состоянии с l =0, следовательно, у него 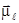и 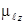равны нулю. Чтобы объяснить, почему же эти атомы отклоняются магнитным полем Гоудсмит и Уленбек высказали предположение о том, что электроны обладают собственным моментом импульса и магнитным моментом (спином).

По аналогии собственный момент импульса электрона стали определять, используя формулу:

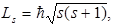
где s – спиновое квантовое число, проекция же спинового момента импульса на направление поля 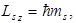где число проекций на направление поля z равно (2 s +1). Так как из эксперимента следовало, что 2 s + 1 = 2, то s = 1/2 и m_s = ± ½.

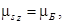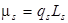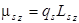Из эксперимента следовало, что а так как и то

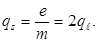
Спиновое гиромагнитное отношение в 2 раза больше орбитального гиромагнитного отношения. Поэтому и говорят, что спин обладает «удвоенным» магнитным моментом.

Лекция 11

Дата добавления: 2014-01-11