Привести примеры типовых спектрально эффективных сигналов и соответствующие значения расстояния между сигналами

Бинарные противоположные сигналы.

В этом случае М =2, т.е. требуется образование сигналов S(t, x₁) и S(t, x₂), достаточно N =1. Векторы

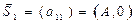
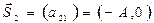
направлены противоположно друг другу

,

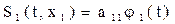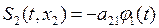
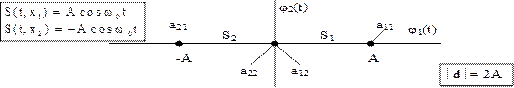
R= -1

Рис.3.7. Вершины векторов бинарных противоположных сигналов.

Бинарные ортогональные сигналы.

В этом случае при М=2 достаточно N=2.

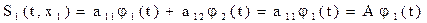
Рис.3.8. Вершины векторов бинарных ортогональных сигналов.

Бинарные ортогональные сигналы обеспечивают меньшее расстояние между концами векторов, чем противоположные сигналы. Однако на практике иногда такого рода сигналы используются.

М-арные ортогональные сигналы.

В этом случае N=M, и число ортогональных функций численно равно размеру алфавита. Каждому x_i соответствует своя j_j, т.е.

……………….

.

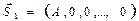
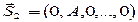
При этом, j_j(t) могут быть ортогональные гармонические функции и

x₁ передаётся сигналом .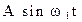

x₂ передаётся сигналом .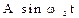

……………………………………

x_N передаётся сигналом .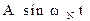

Для удовлетворения условия ортогональности частоты w₁, w₂,..., w_N должны быть кратны частоте 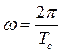. Только в этом случае

,

где n и m - целые числа и R=0.

Биортогональные сигналы.

Пусть М - размер алфавита - чётное число. Образуем ортогональных сигналов 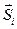. Кроме того, для каждого 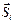сигнала образуем противоположный ему сигнал .

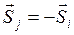Для N = 2:

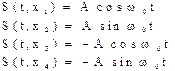
Рис.3.9. Вершины векторов биортогональных сигналов.

Сигналы с прямоугольной конфигурацией векторов.

Для образования такого рода сигналов берётся N колебаний j_j(t). Размер алфавита М при этом может быть равен 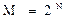. При этом геометрическая конфигурация векторов выбирается такой, чтобы концы векторов находились в вершинах N-мерного куба.

Например, при N=2

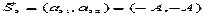
Двумерный куб (квадрат)

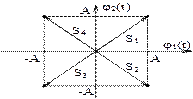
Рис.3.10. Вершины векторов сигналов с прямоугольной конфигурацией векторов.

Пример реализации функции j_j(t) и соответствующих сигналов при N=2, М =4 представлен на рис.3.11.

Рис.3.11. Пример реализации функции j_j(t) исигналов с прямоугольной конфигурацией векторов.

10. Почему и для чего применяют НЧ корректор АЧХ вида 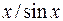и приподнятого косинуса в спектрально эффективных системах?

Спектр синхронного телеграфного сигнала БВН равен

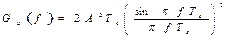(4.2)

с нулями на частотах f_k=kf_c=k/T_c, k =±1,±2,… и занимает достаточно широкую полосу частот. Для уменьшения внеполосных излучений и удельных затрат полосы частот - β_∆f применяют НЧ фильтрацию модулированной огибающей сигнала, например, сигнала БВН. Однако при этом имеют место межсимвольные искажения (МСИ).

Вместе с тем, согласно теореме Котельникова и математической модели ряда (2.15), если на ФНЧ с прямоугольнойАЧХ и частотой среза F_в = f_с /2(Гц) подавать модулирующие δ -импульсы с частотой следования f_с , то можно получить минимум β_∆f. При этом отклики вида sinx/x на эти импульсы можно наблюдать в моменты kT_c независимо и без МСИ.

Однако реальные прямоугольные импульсы сигнала БВН имеют амплитудный спектр вида sinx/x и отличается от равномерного спектра δ - импульса. В этом случае достаточно АЧХ идеального ФНЧ (2.16´) дополнить корректором с АЧХ вида х / sinx и можно получить β_∆f= 0,5[с Гц/симв.] без межсимвольных искажений. Однако АЧХ идеального ФНЧ не реализуема.

Вместе с тем, согласно теореме Найквиста о частичной симметрии: реализуемФНЧ с линейной ФЧХ и симметричной АЧХ относительно частоты Найквиста F_в=f_с/2, который сохраняет моменты пересечения импульсной характеристики с нулевой осью, т.е. так же отсутствуют межсимвольные искажения.

Одной из аппроксимирующих функций этой АЧХ является функция приподнятого косинуса (косинус на пьедестале). Выражение для этой функции, объединенное с характеристикой амплитудного корректора вида х / sinx имеет вид

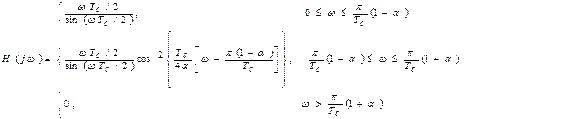(4.3)

где α -коэффициент скругления (рис.4.4). При α = 0 ФНЧ с минимальной полосой f_в =1/2 Т_с нереализуем. При α =1 ширина полосы ФНЧ в 2 раза шире минимальной теоретической.

11. В какой части модулированного радиосигнала закодирована информация источника сообщений?

Из этого выражения следует, что передаваемая информация b_i сигнала u(t), закодирована в комплексной огибающей

12. Огибающая модулированного сигнала ФМ-2 величина действительная или комплексная?

С учетом общего описания ФМ сигналов (4.4),(4.5) для ФМ-2 на интервале 0 ≤ t ≤ Т_с должны выполнятся соотношения:

для фазы: φ[u(t)] ≡ 0 при u(t) =1, φ[u(t)]≡ π при u(t) ≡ -1, соответственно для комплексной огибающей:

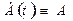при u(t) =1, 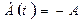при u(t)≡-1.

Т.о. комплексная огибающая ФМ-2 принимает два значения А и –А на действительной оси комплексной плоскости (сигнального созвездия) и совпадает с b(t).

Дата добавления: 2014-01-11