Моделирование

1. Имитируем удар, то есть мысленно нанесем удар по объекту путем определения координат взрыва. В силу идентичности закона рассеивания и его характеристик с законами распределения случайных чисел такими координатами могут быть 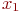и 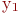, взятые из последовательностей случайных чисел.
2. Вычислим расстояние 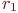от места взрыва ракеты до цели:

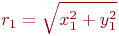
1. Оценим результаты имитации удара, то есть установим факт поражения или непоражения объекта:
• если 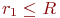, то объект поражен;
• если 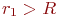, то объект непоражен.
2. Если объект поражен, запомним этот факт увеличением 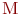на единицу, то есть 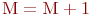(в начале ).
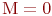3. Для нахождения вероятности поражения объекта повторим имитацию нанесения удара 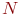раз.
4. Оценим вероятность через частость поражения объекта:

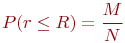
Возможность оценки вероятности частостью доказывается теоремой Я. Бернулли: при неограниченном числе однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте (Бернулли Якоб 1 - самый старший из восьми представителей этой швейцарской семьи - выдающихся ученых).

Чем больше число 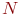(число реализаций, число испытаний, число прогонов модели), тем точнее будет оценка вероятности .

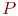В рассмотренном примере 3.1 при 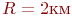, , 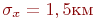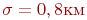оценки вероятностей 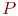поражения цели при различном числе реализаций модели показаны в табл. 3.1.

Таблица 3.1. Оценки вероятностей поражения цели
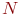
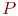
	0,8	0,75	0,7615	0,7644

При 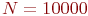, тех же характеристиках рассеивания и других радиусах поражения 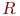получим:

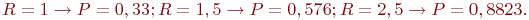
В одной из последующих тем мы установим количественную связь между числом реализаций модели 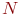, требуемой точностью и доверительной вероятностью результата моделирования, в данном случае оценки вероятности .

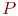Данный пример иллюстрирует сущность метода имитационного моделирования, который заключается в следующем.

1. Создается модель, поведение которой подчиняется тем же вероятностным законам, что и интересующий нас процесс.
2. По известным законам распределения для отдельных характеристик процесса выбираются их случайные значения.
3. Вычисляются параметры исхода процесса при случайных значениях характеристик, полученных на этапе 2, и запоминаются. Этапы 2 и 3 соответствуют одному статистическому испытанию.
4. В результате 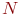статистических испытаний (повторений этапов 2 и 3) получают 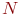значений параметров исхода процесса. Вероятностные характеристики параметров исхода процесса получают в результате статистической обработки полученных случайных величин.

Статистическая обработка и оценка точности результатов моделирования основываются на предельных теоремах теории вероятностей: теореме Чебышева и теореме Бернулли.

Рассмотрим еще один пример.

Пример 3.2. Транспорт 1 с грузом отправился из пункта А в пункт С через пункт В. Одновременно из пункта D в пункт Е через пункт В отправился транспорт 2. Скорости движения транспортов распределены по нормальному закону с математическими ожиданиям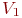и и 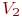и стандартными отклонениям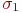и и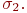

Построить алгоритм имитационной модели (ИМ) с целью определения вероятности встречи транспортов 1 и 2 в пункте В. Расстояние от пункта А до пункта В 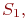а от пункта D до пункта В - 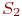.Событие встречи считать состоявшимся, если их времена прибытия в пункт В либо равны, либо отличаются на величину, не превышающую .

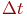Решение

Построим схему движения транспортов 1 и 2 (рис. 3.2).

Возьмем две последовательности нормально распределенных случайных чисел:

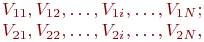
характеристики которых соответствуют матожиданиям и стандартным отклонениям скоростей движения транспортов 1 и 2.

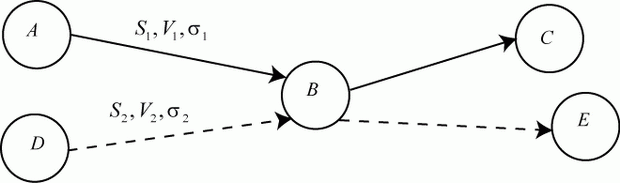
Рис. 3.2. Схема движения транспортов

1. Имитируем движение транспортов 1 и 2 до пункта В со скоростям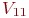и и 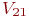соответственно, взятыми из последовательностей нормально распределенных случайных чисел.
2. Вычислим время 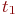и 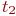прибытия в пункт В транспортов 1 и 2 соответственно:

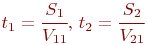
1. Оценим результат имитации движения транспортов 1 и 2, т. е. установим факт наличия или отсутствия их встречи:
• если 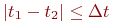, встреча состоялась;
• если 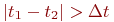, встреча не состоялась.
2. Если встреча состоялась, зафиксируем этот факт увеличением значения 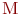на 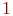, т. е. 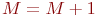(вначале ).
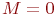3. Для нахождения вероятности встречи транспортов 1 и 2 повторим имитацию их движения 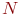раз.

Рассчитаем вероятность встречи:

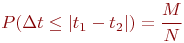
Результаты моделирования при 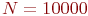и характеристиках движения транспортов: , , :

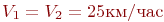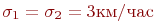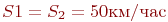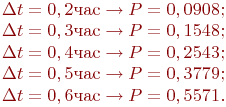
Очевидно, изложенный процесс имитации легко может быть реализован на компьютере. Представим алгоритмы моделей примеров 3.1 и 3.2 схемами (рис. 3.3 и 3.4).

В рассмотренных примерах исследуются различные процессы. Но алгоритмы моделей этих процессов (для сравнения рядом с алгоритмом задачи 3.2 (рис. 3.3) показан и алгоритм задачи 3.1 (рис. 3.4) имеют общую, практически идентичную часть (блоки 1, 5…8, на рис. 3.3 и 3.4 они выделены) и часть, которая непосредственно имитирует исследуемый процесс (блоки 2… 4).

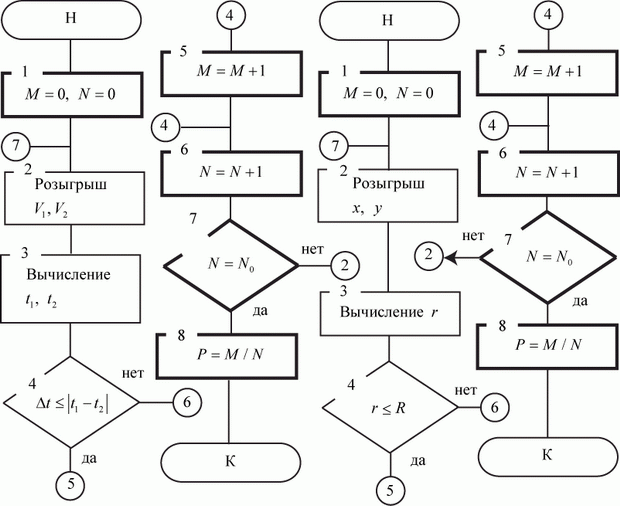
увеличить изображение
Рис. 3.3.

Подобное сходство и различие еще раз подтверждают сформулированную нами ранее сущность имитационного моделирования.

Пример 3.3. По объекту наносится не одиночный, а три последовательных ракетных удара. При поражении объекта любой ракетой пуски прекращаются. Остальные условия те же, что и в примере 3.1.

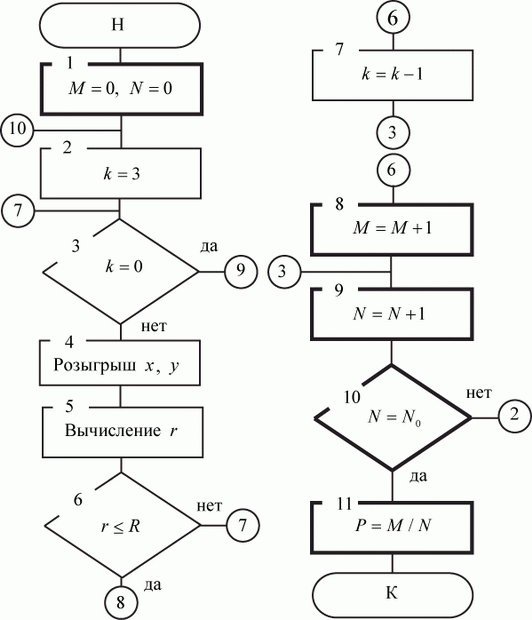
Алгоритм ИМ приведен на рис. 3.5. На нем выделены блоки 1, 8…11, выполняющие те же функции, что блоки 1, 5…8 в алгоритмах ИМ на рис. 3.3 и 3.4. Блоки 2…7 непосредственно имитируют нанесение удара по объекту, т. е. выполняют одну реализацию (один прогон модели). В блоке 2 переменной 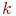присваивается начальное число пусков ракет. Далее эта переменная используется для организации внутреннего цикла по числу пусков. После каждого пуска значение k уменьшается на 1 (блок 7). При 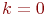(блок 3) реализация завершается. Завершается она также и при поражении объекта (блок 6). Но при этом предварительно значение переменной 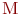увеличивается на 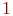. По завершении 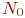реализаций рассчитывается оценка математического ожидания вероятности поражения объекта тремя последовательными пусками ракет.

увеличить изображение
Рис. 3.5. Алгоритм модели нанесения удара тремя ракетами

Как отмечалось вначале, название метода - имитационное моделирование не очень удачно в том смысле, что несет в себе тавтологию: моделирование и есть имитация. Однако название прижилось. Очень часто метод называют статистическим моделированием из-за необходимости статистической обработки накапливаемого результата - в случае вероятностных операций.

Иногда статистическое моделирование называют "метод Монте-Карло", по городу, где процветает игра в рулетку, исход которой случаен и образуется своеобразным датчиком случайных исходов - рулеткой.

Дата добавления: 2014-01-11