Средняя квадратичная

Средняя простая

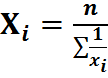(4)

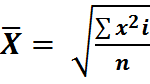(5)

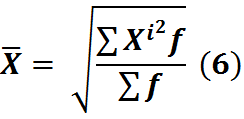
Применяется когда производство либо =1 либо одинаково

Кроме производственного среднего применяется среднее геометрическое, будет далее ряды динамики для определения средних размеров – используют средне кубическое.

Средне геометрические будут далее в теме «геометрические динамики»

Применятся для определенных средних размеров,

Свойства средней арифметической:

Вычисление среднеарифметического частного сопряженного с большими затратами времени. Процедуру расчета можно упростить, если выскользнув след свойствами:

1)Ср. арифметические из пост чисел= этому постоянному.

2)Если все пропорционально изменить, то средне арифметическое не изменится.

3)Если все варианты уменьшить или увеличить на одно и тоже число, то все уменьшится или увеличится на одинаковое кол-во раз.

4)Если все варианты увеличится или уменьшить в один число раз, то среднее тоже увеличится или уменьшится в тоже число раз.

Таблица 1

№	Районы Брянска	Число школ	Ср. число уч в шк	Средне чисто уч приходит.
	Бежецкий
	Советский
	Володарка
	Фокинский
		Х1?	Х2?	Х3?

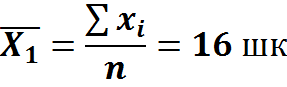
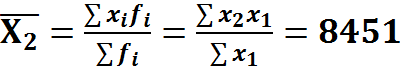в школе

Среднее число учащихся на 1 учителя = среднее число учащихся в школах/ среднее число учащихся приход на 1 учит

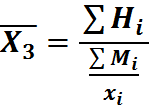
Лекция №6 Дата: 8.10.12

Тема 6: Структурные средние

Помимо средних существует система структурных показателей: мода и

Медианна

М (мода) наиболее часто встречающийся вариант ряда

В дискретном ряду мода определяется, как значение признака с наиболее частной без вычисления определения моды не представляет трудностей.

Таблица 1

Размер обуви								итого
Число пар

1.1 Модой является 35 размер обуви.так как этого размера больше всего

1.2 Мода для инертно ряда определяется по приблизительной формуле

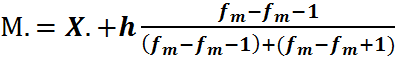(1)

Х.- нижняя граница предельного интегрирования

h - величина

Fm – частного модельного интегрирования

Fm-₁ –предмет модельного

Fm+₁ – предмет следующий за модельным

Распространение студентов по возрасту Таблица 1

Возрастные группы	До 20	20-25	25-30	30-35	35-40	40-45	>45
Число студентов
Сумма неконечных подсчетов

Для начисления модуля в интервальном ряду в начале определяют модульный интервал, в пределах которого находится мода

Затем находят приближенное значение модальной величины признака по формуле (1)

Т.к на интервале 25-30 существует наиболее частного (1054) модельный интервал будет находится в этих пределах.

M.=1054-872/25+5(1054-872)+(1054+781)= 27 (лет)

Это означает, что модульный возраст составляет 27 лет.

Это означает,т.о мода наиболее привычная величина распределения.

Мода- средняя величина по-разному характеризуют совокупности в целом и мода по обобщающему значению уступает ей.

Мода- это описательная характеристика, она описывает количество, структуру, строение

Ме( медиана) – это вариант который приходит на середину ряда, расположенного в порядке возрастания или убывания чисел значений признаков.

Медиана делит ряд на 2 равные части.

Для интервального вариационного ряда алгоритм определения методологии в следующем.

1) Определить модельный интервал на которою приходится медиана.

2) По приближенной формуле определим медиану.

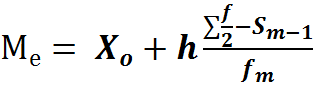(2)

Х₀- нижняя граница интервала который содержит медиану.

H - величина интервала.

Сумма∑ F - сумма частот или число членов ряда

Sm-₁ – сумма накопленных частот для предшествующая медианному.

Fm – частота медианного интервала.

Сумма∑ F = 3 462

Сумма ∑F/2 = 1731

Это означает, что медиальный интервал находится в переделах 35-30 лет

Ме= 25+5=1731-1216/154=27,4(лет)

Это означат что одна половина имеет возраст до 27,4 лети, а вторая больше.

Медиана, так же ка и мода является,описательной характеристикой.

Дата добавления: 2014-01-11