Основні інформаційні характеристики дискретних джерел повідомлень

Вступ

Час – 4 год.

Навчальні питання

Лекція 11(3.1). Двійкові коди з виявленням та виправленням однократної помилки

1.... Основні інформаційні характеристики дискретних джерел повідомлень. 1

2.... Коди, їх класифікація та основні характеристики. 3

3.... Двійкові коди, що виявляють помилки. 6

4.... Двійкові коди, що виправляють однократні помилки. 11

Література.

1. Жураковський Ю.П., Гніліцький В.В. Теорія інформації та кодування в задачах: Навчальний посібник. – Житомир: ЖІТІ, 2002, с. 121 – 126, 131 – 142.

В першому питанні пригадаємо основні положення теорії інформації та кодування, а далі почнемо розглядати коди, що виявляють помилки

Дискретне джерело інформації – це таке джерело, яке може виробити (згенерувати) за скінчений відрізок часу тільки скінчену множину повідомлень. Кожному такому повідомленню можна співставити відповідне число, та передавати ці числа замість повідомлень.

Дискретне джерело інформації є достатньо адекватною інформаційною моделлю дискретних систем, а також неперервних систем, інформаційні сигнали про стан яких піддають аналого-цифровому перетворенню; таке перетворення виконується в більшості сучасних автоматизованих систем управління.

Первинні характеристики дискретного джерела інформації – це

· алфавіт,

· сукупність ймовірностей появи символів алфавіту на виході дискретного джерела

· та тривалості символів.

Алфавіт – множина 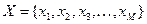символів, які можуть з’явитися на виході дискретного джерела; 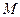– потужність, тобто кількість різноманітних символів алфавіту.

Якщо всі ймовірності, які визначають виникнення символів на виході джерела, не залежать від часу, джерело називають стаціонарним.

Для опису джерел, які не мають пам’яті, достатньо мати значення безумовних ймовірностей p (x_i) виникнення символів x_i, i =1, 2, 3,…, M на його виході.

Більшість реальних джерел інформації є джерелами з пам’яттю. Розподіл ймовірностей виникнення чергового символу на виході дискретного джерела з пам’яттю залежить від того, які символи були попередніми. Таке джерело інформації називають марковським, оскільки процес появи символів на його виході адекватний ланцюгам Маркова; останні в свою чергу отримали таку назву на честь російського математика Маркова (старшого) Андрія Андрійовича (1856 – 1922), який заклав основи розділу теорії випадкових процесів.

Кількість інформації – одне із основних понять теорії інформації, яка розглядає технічні аспекти інформаційних проблем, тобто вона дає відповіді на запитання такого типу:

· якою повинна бути ємність запам’ятовуючого пристрою для запису даних про стан деякої системи,

· якими повинні бути характеристики каналу зв’язку для передачі певного повідомлення

· тощо.

Кількісна оцінка інформації пов’язана з поняттям ентропії. Ентропія є мірою невизначеності, непрогнозованості ситуації. Зменшення ентропії, що відбулось завдяки деякому повідомленню, точно збігається з кількістю інформації, яка міститься в цьому повідомленні.

Для дискретного немарковського (без пам’яті) джерела інформації ентропія 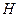визначається за таким виразом:

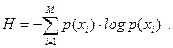
(1.1)

Зазначимо, що 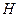не залежить від того, якими є випадкові події або величини (якщо 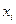– випадкова величина), а визначається тільки значеннями ймовірностей. Це означає, що ентропія є характеристикою розподілу ймовірностей.

Значення 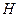показує, яку кількість інформації в середньому дає поява одного символу на виході дискретного джерела інформації. Ця міра запропонована американським математиком і інженером Клодом Шенноном.

Якщо основа логарифма в (1.1) дорівнює двом, то одиниці вимірювання H, а також кількості інформації називають бітами або двійковими одиницями.

Ентропія дискретного розподілу ймовірностей завжди невід’ємна і набуває максимального значення H_max, коли всі мають однакові значення:

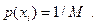
(1.2)

В цьому разі маємо міру кількості інформації, яку ще до Шеннона було запропоновано англійським математиком Р.Хартлі. Підставимо (1.2) в (1.1), отримаємо

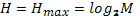. (1.3)

Значення H_max збігається з кількістю двійкових комірок пам’яті, які необхідно мати, щоб зафіксувати за допомогою двійкового коду інформацію про один із M можливих станів системи, або про символ, що з’явиться на виході дискретного джерела інформації.

Ентропія дорівнює нулю, якщо ймовірність появи одного з символів є одиниця (при цьому, звичайно, ймовірність появи будь - якого іншого символу буде дорівнювати нулю); в такій ситуації невизначеність відсутня.

Продуктивність 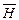джерела інформації – це кількість інформації, що виробляється джерелом за одиницю часу:

,

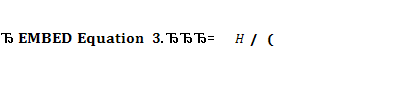(1.4)

де 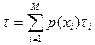– середня тривалість символу, 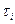– тривалість символу .

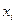Надмірність (надлишок) R дискретного джерела інформації дає відносну оцінку використання потенційних можливостей джерела з алфавітом заданої потужності :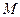

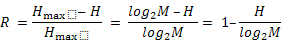
(1.5)

Надмірність може приймати значення від 0 до 1. Вона дорівнює нулю, якщо 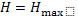; в цьому випадку дискретне джерело інформації буде виробляти максимально можливий інформаційний потік. Із першої теореми Шеннона виходить, що при застосуванні ефективного кодування надмірність може бути зведена практично до нуля, внаслідок чого об’єм повідомлення буде зменшено майже в 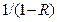разів.

Ентропія, продуктивність та надмірність – інтегральні інформаційні характеристики дискретного джерела інформації.

Дата добавления: 2014-01-11