Примеры. Процессы массового обслуживания в экономических системах

Процессы массового обслуживания в экономических системах. Потоки, задержки, обслуживание. Формула Поллачека-Хинчина.

Большинство экономических систем модно представить как систему массового обслуживания.

а) Автозаправочная станция (линия – бензоколонка, заявки – машины).

б) Телефонная станция (линии – каналы связи, заявки – вызовы абонента).

в) Парикмахерская (линии – мастера, заявки – клиенты).

Системы массового обслуживания (СМО) - это обобщенное название объектов определенной структуры, имеющих заданные связи и взаимодействующие ("обслуживающие") с неограниченным числом перемещаемых особых объектов, называемых "требованиями" или "заявками" [5]. В качестве типичного примера СМО принято рассматривать телефонную сеть, имеющей в качестве связанных элементов структуры - коммутаторы, а в качестве требований - телефонные вызовы. Более современный пример - сеть ЭВМ, для обмена пакетами информации. Структура простейшей СМО и пример более сложной структуры приведены на рис.1.1

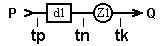
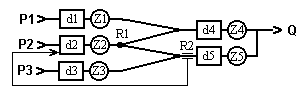
Рис.1.1. Структура простейшей и более сложной СМО.

Основные элементы СМО: Р - входной поток требований, d1 - очередь (накопитель) поступающих требований, Z1 – обслуживающая система, Q – поток обслуженных требований, R1 - элемент деления потока требований, R2 - элемент организации обратного потока требований. Процесс обслуживания каждого i-того требования в простейшей СМО характеризуется следующими моментами времени: 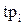- время прибытия, 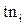- начало обслуживания, 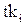- время конца обслуживания.

Входной поток требований P задаётся вектором 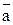, компонентами которого являются интервалы между поступающими заявками. Каждому поступившему требованию соответствует некоторая длительность его пребывания в очереди 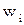и длительность обслуживания 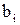, которые образуют соответственно вектора 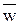и 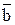. Перечисленные параметры описывают процесс прохождения требования через два уровня СМО, что иллюстрирует диаграмма на рис.1.2.

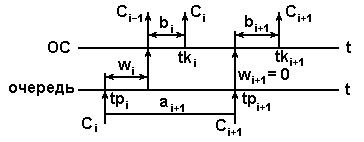
Рис.1.2. Диаграмма процесса работы простейшей СМО.

Время прибытия 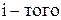требования равно:

.

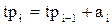Время конца обслуживания 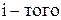требования определяется выражением:

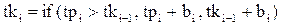
Для индикации факта нахождения 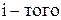требования в СМО используется функция присутствия требования к системе:

,

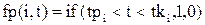где t – текущее непрерывное время.

Количество требований в системе в момент времени t определяется следующим образом:

.

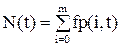Дисциплина СМО - это порядок принятия заявок в очередь или к обслуживанию.

СМО является системой с отказами, если в ней существуют очереди с ограниченным временем пребывания заявки. После истечения допустимого интервала заявки могут исчезать из системы или возвращаться к её входному потоку. Возможные правила дисциплин:

1. Линии занимаются в порядке прибытия заявок.

2. Заявки извлекаются из очереди в произвольном порядке.

3. Заявки применяются к обслуживанию по минимальному остатку длительности ожидания.

4. Заявки принимаются к обслуживанию, по какому-либо вторичному признаку заявки.

Моменты поступления требований и длительности их обслуживания - случайные величины. Если законы распределения этих случайных величин известны, то используется следующая система обозначений простейших СМО:

A/B/m/K/M,

где А - тип закона распределения интервалов между соседними требованиями,

В - тип закона распределения длительности обслуживания требований,

m - количество однотипных параллельных обслуживающих систем,

К - емкость накопителя (очереди),

М - мощность источника требований (количество телефонных аппаратов, подключенных к коммутатору).

Обозначение типов законов распределения:

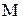- показательное распределение: ,

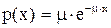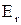- распределение Эрланга,

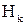- гипергеометрическое распределение,

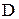- равномерное распределение,

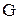- произвольное распределение.

Основные соотношения теории СМО:

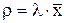- где 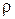- коэффициент использования СМО, 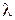- средняя скорость поступления требований, 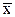- среднее время обслуживания.

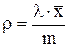- коэффициент использования СМО, состоящей из 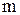приборов.

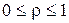- условия стабильности работы СМО.

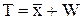- среднее время пребывания требования в системе, W – среднее время пребывания в очереди.

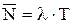- формула Литтла, 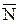- среднее число требований в системе.

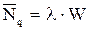- средняя длина очереди.

Рассмотрим пример использования треугольного распределения. Пример связан с динамическими характеристиками системы управления базами данных (СУБД) в экономической информационной системе.

Пример. Предположим, что база данных находится на компьютере, не входящем в состав какой-либо вычислительной" сети. Поэтому пользователь, работающий с этой базой, имеет во время работы монопольный доступ к ней. Известны структуры и частоты запросов пользователей к этой базе данных. Рассмотрим три случая физической организации базы данных (рис. 1.3).

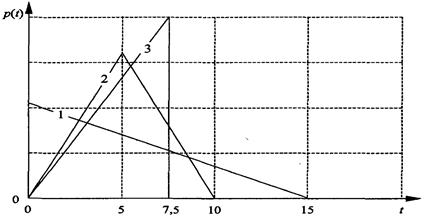
Рис.1.3. График плотности вероятностей для треугольного распределения:

1 - максимум слева; 2 - максимум в центре; 3 - максимум справа

Первый случай. Допустим, что администратор базы данных (системный программист) осуществил физическую организацию данных, которая обладает следующими свойствами:

• наиболее вероятное время ответа на запрос близко к 0 с;

• минимальное вероятное время ответа не менее 0 с;

• максимальное вероятное время ответа не превьппает 15 с;

• распределение вероятностей представлено линией 1 на рис. 1.6.

Этот системный программист обеспечил минимальное время для наиболее вероятных запросов за счет увеличения времени для менее вероятных. Среднее время получения ответа в этом случае t = 5 с.

Второй случай. Администратор базы данных по просьбе пользователей

решил уменьшить время ответа на те запросы, которые редко возникают. Для этого он переделал физическую организацию данных и получил следующие ее свойства:

• наиболее вероятное время ответа на запрос равно 5 с;

• минимальное вероятное время ответа не менее 0 с;

• максимальное вероятное время ответа не преЬьпиает 10 с;

• распределение вероятностей показано линией 2 на рис. 1.6.

Таким образом, системный программист обеспечил снижение времени ответа для менее вероятных запросов за счет увеличения времени ответа для наиболее в^оятных. Среднее время получения ответа осталось тем же: t = 5 с.

Третий случай. Администратор базы данных решил еще более уменьшить время ответа на менее вероятные запросы. Для этого он опять переделал физическую организацию данных и получил следующие свойства:

• наиболее вероятное время ответа на запрос равно 7,5 с;

• минимальное вероятное время ответа не менее 0 с;

• максимальное вероятное время ответа не превышает 7,5;

• распределение вероятностей изображено линией 3 на рис. 1.6.

Этот системный программист обеспечил дальнейшее снижение времени ответа для менее вероятных запросов за счет увеличения времени ответа для более вероятных. Среднее время получения ответа и в этом случае не изменилось: t = 5 с.

Возникает естественный вопрос: «Какая физическая организация лучше?». Если отбросить факторы, определяющие большую или меньшую важность запросов, и вспомнить, что база данных не имеет множественного доступа из вычислительной сети, то можно утверждать, что все три способа организации данных одинаковы, так как пользователи этой базы имеют одно и то же среднее время ответа.

Однако если подключить компьютер с нашей базой к локальной вычислительной сети и разрешить доступ к базе данных большому числу пользователей этой сети из рабочих компьютеров этих пользователей, то необходимо учитывать возникновение очереди запросов к базе данных при ее монопольном использовании. Предположим, что число пользователей довольно велико и выполняются условия предельной теоремы о суперпозиции потоков событий (в нашем случае возникновение запроса к базе данных – это событие). Тогда поток запросов к базе простейший (экспоненциальное распределение интервала поступления). Поэтому выполняются условия, при которых справедлива следующая формула для

оценки средней задержки запросов в очереди (формула Поллачека- Хинчина):

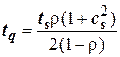
где t_q - искомая средняя задержка в очереди; t_s - среднее время обслуживания;

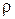- загрузка обслуживающего узла (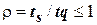); с_s;- коэффициент вариации времени обслуживания.

Если известно среднеквадратичное отклонение времени обслуживания

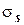, то c_s = 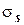/ t_s. В трех рассмотренных случаях t_s = t = 5c. Загрузка не изменяется, так как поток запросов к базе данных тот же самый. Однако разброс значений в первом случае примерно в 3 раза больше, чем в третьем. Соответственно с_s может быть больше приблизительно в 9 раз (т.е. на порядок!), а это часть множителя в числителе формулы.

После этого можно сделать вывод, что задержка в очереди в первом

случае будет значительно больше, чем в третьем. Во втором случае задержка в очереди также будет превосходить задержку, возникающую в третьем случае. Поэтому наиболее рациональным относительно возникающих задержек является третий способ организации базы данных.

Дата добавления: 2014-01-11