
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделирование нормального распределения
|
|
|
|
Будем обозначать через 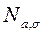 - случайную величину, распределенную по нормальному закону с плотностью
- случайную величину, распределенную по нормальному закону с плотностью

Если а=0, 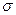 =1, то говорят о стандартной нормальной случайной величине, которую обозначим N. Связь между
=1, то говорят о стандартной нормальной случайной величине, которую обозначим N. Связь между 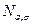 и N простая:
и N простая:
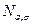 =a+
=a+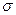 N
N
Поэтому достаточно имитировать N. Разработаны многочисленные способы имитации этой величины. Рассмотрим некоторые из них.
Метод полярных координат.
Утверждение. Пусть Х и У независимые случайные величины со стандартным нормальным распределением. Рассмотрим случайную точку на плоскости - (Х,У) и ее полярные координаты 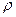 и
и 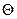 :
:

 (9.1)
(9.1)
Тогда 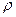 и
и 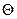 будут независимыми случайными величинами, распределенными по следующим законам:
будут независимыми случайными величинами, распределенными по следующим законам:
- имеет функцию распределения 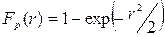
- распределена равномерно на [0,2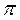 ].
].
Наоборот, если 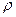 и
и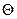 имеют указанные распределения и независимы, то величины Х и У, вычисленные по формулам (9.1), независимы и имеют стандартное нормальное распределение. Доказательство очевидно из следующих преобразований:
имеют указанные распределения и независимы, то величины Х и У, вычисленные по формулам (9.1), независимы и имеют стандартное нормальное распределение. Доказательство очевидно из следующих преобразований:
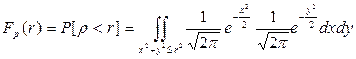 =
=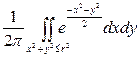 = =
= =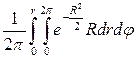 =
=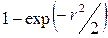
И обратно
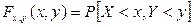 =
=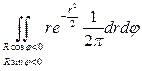 =
=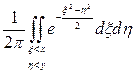 = =
= =

Рассмотрим способ имитации. Используя метод обратной функции, получим
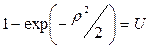 Откуда
Откуда 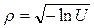
Полярный угол 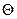 получается по формуле
получается по формуле 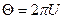 . Окончательно алгоритм имитации будет следующий
. Окончательно алгоритм имитации будет следующий
- от ДСЧ получаем 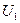 и
и 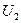 .
.
- вычисляем сразу пару значений N:
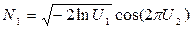 ,
, 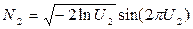 .
.
Приведенный метод имитации N является точным, легко программируется и точно работает. Известен как метод Бокса и Маллера.
Известна модификация этого метода, дающая точные результаты быстрее. По этому методу генерируются два случайных числа 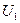 и
и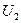 . Далее полагая
. Далее полагая  и
и 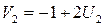 , вычисляют
, вычисляют 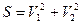 . При
. При 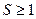 начинают цикл снова. При S<1 вычисляют
начинают цикл снова. При S<1 вычисляют
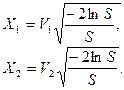
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 261; Нарушение авторских прав?; Мы поможем в написании вашей работы!