Оценка точности и необходимого количества реализаций модели

Определим необходимое число прогонов модели для достижения заданной точности вычислений в связи с оценкой вероятности повторения некоторого события.

Пусть требуется по результатам моделирования найти вероятность p некоторого события А. Например, вероятность поступления k заявок в СМО в течение определенного срока и т.п.

Произведем N прогонов модели, фиксируя каждый раз появление или непоявление события А. Пусть событие А зафиксировано при М прогонах. Тогда оценкой для вероятности p служит частота p~ =М/N.

Эта оценка несмещенная М[p~]=p. В курсе теории вероятностей доказывается интегральная предельная теорема

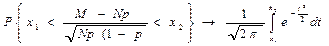
Эта теорема фактически утверждает, что оценка p~ асимптотически нормальна. Поясним на примере. Пусть

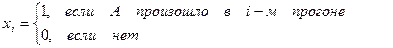
Тогда M[Xi]=1p+0(1-p)=p; D[Xi]=(1-p)(1-p)p+(0-p)(0-p)(1–p)=p(1-p)

М=х1+х2+х3+...+хN

p=М/N

М[p]=Д{M[x1]+M[x2]+...+M[xN]}=- Д (p+p+...+p)=p

D[p~]=Д{D[x1]+D[x2]+...+D[xn]}=Д p(1-p)

Асимптотическая нормальность означает, что

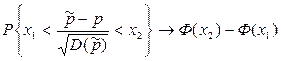
Подставляя сюда найденные оценки, получаем формулировку интегральной теоремы.

Воспользуемся асимптотической нормальностью для оценки N количества прогонов, необходимых для достижения заданной точности вычисления оценки p. При уровне доверительной вероятности 1-a. Из условия асимптотической нормальности следует

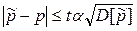
Потребуем, чтобы правая часть не превосходила e, получим

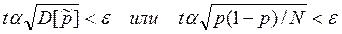
Откуда .

В этой формуле t_а находится по таблицам нормального закона, e - заданная точность. Выражение p(1-p) неизвестно, т.к. p - это и есть разыскиваемая вероятность. Но нетрудно избавиться от p. Рассмотрим график этой функции на отрезке 0<p<1 (рис. 10.2).

Рис.10,2

Из графика видно, что p(1-p)<1/4. Требуемая точность будет достигаться, если взять . Эта оценка может оказаться сильно завышенной при p, близких к 0 и 1.

Пример. Пусть p близко к 0,1. p(1-p)=0.1*0.9=0.09;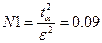

Рис.10.3. Схема обработки данных с использованием правил автоматической остановки

, т.е. использование грубой оценки увеличивает число прогонов почти в 3 раза.

В этих случаях рекомендуется последовательная процедура, состоящая в следующем:

I. Вначале осуществляют небольшое число прогонов Nо(Nо=100-200), и оценивают p~ по этим прогонам.

2. Рассчитывают и окончательно оценивают p по N прогонам.

Возможна и другая схема вычислений, в которой N заранее не рассчитывается. Схема вычислений представлена на рис.11.3. N - номер прогона, Nk - номер контрольного прогона. Контроль осуществляется через DN шагов. Вначале осуществляется No прогонов. Условием окончания служит 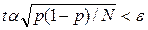где N - вычисленное к данному моменту число прогонов, p - полученная к данному моменту оценка. Замечание. Описанная методика неприменима, если p слишком близко к нулю или к единице. Тогда можно для оценки p (а также и в любом другом случае) использовать неравенство Чебышева

Это приводит к следующей оценки N:

Полученная оценка довольно грубая, но заведомо надежная. Она может завышать количество прогонов примерно в 5 раз.

Дата добавления: 2014-01-11