
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пусть заданы векторы в прямоугольной системе координат
|
|
|
|
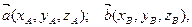 тогда линейные операции над ними в координатах имеют вид:
тогда линейные операции над ними в координатах имеют вид:
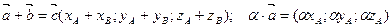
Скалярное произведение векторов.
Определение. Скалярным произведением векторов  и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.

 ×
× = ï
= ï ïï
ïï ïcosj
ïcosj
Свойства скалярного произведения:
1)  ×
× = ï
= ï ï2;
ï2;
2)  ×
× = 0, если
= 0, если  ^
^ или
или  = 0 или
= 0 или  = 0.
= 0.
3)  ×
× =
=  ×
× ;
;
4)  ×(
×( +
+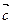 ) =
) =  ×
× +
+  ×
×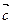 ;
;
5) (m )×
)× =
=  ×(m
×(m ) = m(
) = m( ×
× ); m=const
); m=const
Если рассматривать векторы 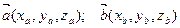 в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то

 ×
× = xa xb + ya yb + za zb;
= xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:

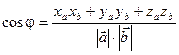 ;
;
Пример. Найти (5 + 3
+ 3 )(2
)(2 -
-  ), если
), если 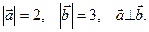
10 ×
× - 5
- 5 ×
× + 6
+ 6 ×
× - 3
- 3 ×
× = 10
= 10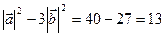 ,
,
т.к. 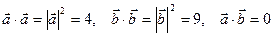 .
.
Пример. Найти угол между векторами  и
и  , если
, если 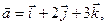
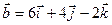 .
.
Т.е.  = (1, 2, 3),
= (1, 2, 3),  = (6, 4, -2)
= (6, 4, -2)
 ×
× = 6 + 8 – 6 = 8:
= 6 + 8 – 6 = 8:
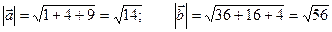 .
.
cosj = 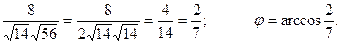
Пример. Найти скалярное произведение (3 - 2
- 2 )×(5
)×(5 - 6
- 6 ), если
), если 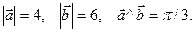
15 ×
× - 18
- 18 ×
× - 10
- 10 ×
× + 12
+ 12 ×
× = 15
= 15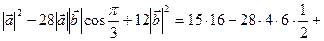
+ 12×36 = 240 – 336 + 432 = 672 – 336 = 336.
Пример. Найти угол между векторами  и
и  , если
, если 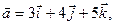
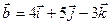 .
.
Т.е.  = (3, 4, 5),
= (3, 4, 5),  = (4, 5, -3)
= (4, 5, -3)
 ×
× = 12 + 20 - 15 =17:
= 12 + 20 - 15 =17:
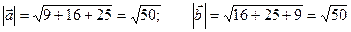 .
.
cosj = 
Пример. При каком m векторы  и
и 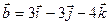 перпендикулярны.
перпендикулярны.
 = (m, 1, 0);
= (m, 1, 0);  = (3, -3, -4)
= (3, -3, -4)
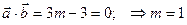 .
.
Пример. Найти скалярное произведение векторов 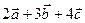 и
и 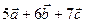 , если
, если 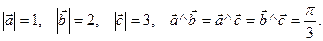
(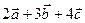 )(
)(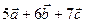 ) =
) = 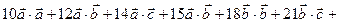
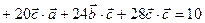
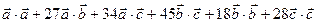 = 10 +
= 10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
Векторное произведение векторов.
Определение. Векторным произведением векторов  и
и  называется вектор
называется вектор 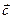 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) 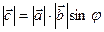 , где j - угол между векторами
, где j - угол между векторами  и
и  ,
,
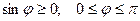
2) вектор 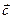 ортогонален векторам
ортогонален векторам  и
и 
3)  ,
,  и
и 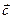 образуют правую тройку векторов.
образуют правую тройку векторов.
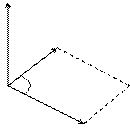 Обозначается:
Обозначается: 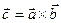 или
или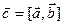 .
.
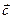

j

Свойства векторного произведения векторов:
1) 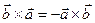 ;
;
2) 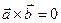 , если
, если  ïï
ïï или
или  = 0 или
= 0 или  = 0;
= 0;
3) (m )´
)´ =
=  ´(m
´(m ) = m(
) = m( ´
´ );
);
4)  ´(
´( +
+ 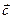 ) =
) =  ´
´ +
+  ´
´ 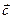 ;
;
5) Если заданы векторы  (xa, ya, za) и
(xa, ya, za) и  (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами
(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами 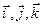 , то
, то

 ´
´ =
=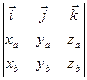
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах  и
и  .
.
Пример. Найти векторное произведение векторов 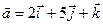 и
и
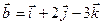 .
.
 = (2, 5, 1);
= (2, 5, 1);  = (1, 2, -3)
= (1, 2, -3)
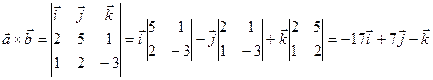 .
.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),
С(0, 1, 0).
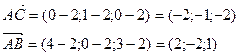
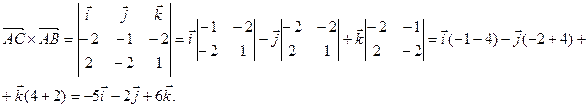
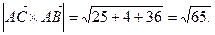
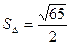 (ед2).
(ед2).
Пример. Доказать, что векторы 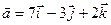 ,
, 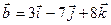 и
и 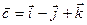 компланарны.
компланарны.
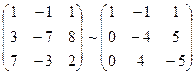 , т.к. векторы линейно зависимы, то они компланарны.
, т.к. векторы линейно зависимы, то они компланарны.
Пример. Найти площадь параллелограмма, построенного на векторах 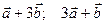 , если
, если 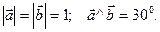
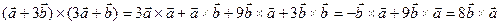
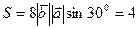 (ед2).
(ед2).
Смешанное произведение векторов.
Определение. Смешанным произведением векторов  ,
,  и
и 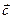 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на вектор, равный векторному произведению векторов
на вектор, равный векторному произведению векторов  и
и 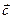 .
.
Обозначается 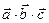 или (
или ( ,
,  ,
,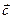 ).
).
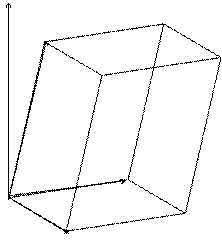
Смешанное произведение 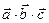 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах  ,
,  и
и 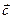 .
.
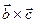

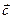

Свойствасмешанного произведения:
1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.
2)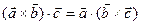
3)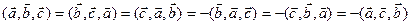
4)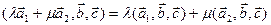
5) Объем треугольной пирамиды, образованной векторами  ,
,  и
и 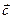 , равен
, равен
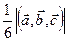
6)Если 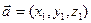 ,
,  , то
, то
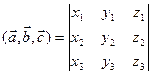
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем координаты векторов: 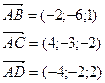
Найдем смешанное произведение полученных векторов:
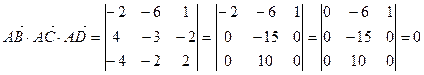 ,
,
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем координаты векторов: 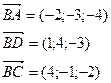
Объем пирамиды 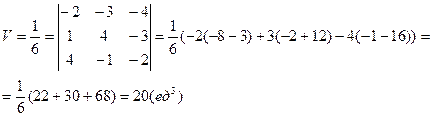
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
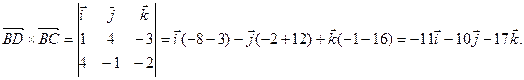
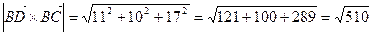
Sосн = 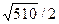 (ед2)
(ед2)
Т.к. V = 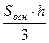 ;
; 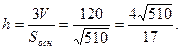 (ед)
(ед)
Аналитическая геометрия.
Уравнение поверхности в пространстве.
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
Общее уравнение плоскости.
Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:

Ax + By + Cz + D = 0,
где А, В, С – координаты вектора 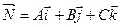 -вектор нормали к плоскости.
-вектор нормали к плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 348; Нарушение авторских прав?; Мы поможем в написании вашей работы!