Растровое представление эллипса

Рассматриваем эллипс, т.к. это более общий случай, из него получается окружность. Если в эллипсе, ориентированном вдоль осей координат, задать одинаковые горизонтальную и вертикальную координаты, окружность не получится, останется эллипс, т.к. в большинстве графических режимов вертикальный и горизонтальный масштабы различны. Точка растра имеет квадратную форму только в видеоадаптерах VGA. Для получения окружности надо рассчитать число пикселов по осям. В библиотеке BGI масштабирование уже проведено. При рисовании эллипса с одинаковыми размерами осей или окружности искажения формы нет. Для каждого графического драйвера и графического режима в BGI имеется коэффициент сжатия.

Как и для прямой, координаты многих пикселов будут иметь аппроксимированное значение, фигура будет "изломанной". Пример - rasrt\ellipse\ex1.cpp.

Как формируется эллипс? Решение "в лоб" - использовать алгебраическое уравнение. Пусть эллипс имеет координаты центра, размеры полуосей и , полуоси параллельны осям x и y. Вид уравнения:

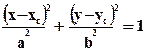
Построение эллипса через уравнение, как и для прямой, нерационально по времени, т.к. вычисления по формуле громоздки, содержат долго выполняющиеся операции умножения, деления, вызов функции извлечения квадратного корня. Пример программы - в [ 3 ].

Итерационный алгоритм для эллипса аналогичен алгоритму Брезенхема для прямой. Изображение формируется попиксельно, очередной пиксел выбирается по критерию близости к истинному значению. Т.к. эллипс симметричен относительно осей координат, достаточно иметь алгоритм формирования изображения в первом квадранте. Далее - симметричное инвертирование координат. Если эллипс не симметричен относительно осей координат, можно привести его к симметричной координатной системе поворотом осей координат. Для пересчета имеются специальные алгоритмы, ссылка на один из них (статья на английском языке) в [ 3 ].

Уравнение простейшего эллипса с центром в начале координат и полуосями b (по оси y) и a (по оси x)

.

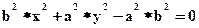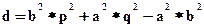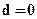Используется так называемый "алгоритм средней точки". Он выбирает, какой из соседних пикселов ближе к эллипсу, вычисляя, находится ли средняя между пикселами точка вне или внутри эллипса. Подставим координаты средней точки в уравнение эллипса: . , если точка лежит на эллипсе, , если точка находится внутри эллипса, 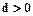, если точка находится вне эллипса. Следовательно, по знаку функции можно определить ближайший пиксел.

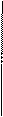А А

М М

В В

Средняя точка М лежит внутри эллипса, Средняя точка М лежит вне эллипса,

выбирается ближайшая точка А. выбирается ближайшая точка В.

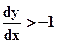Возникает вопрос: какую пару соседних пикселов исследовать на близость? Выбор зависит от наклона касательной к эллипсу. Пусть . Наклон вычисляется как . Если , выбираются соседние вертикальные пикселы. Если 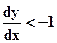, выбираются соседние горизонтальные пикселы.

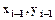
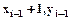
A

М

А М В

B

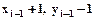
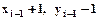
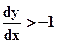
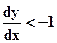
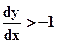
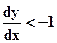
Очередной пиксел выбирается итеративно по отношению к предыдущему пикселу. Если 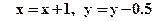. Если . Сравнивая d для двух соседних точек, можно вывести итерационные формулы для d.

При .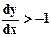

При

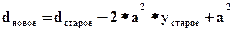
Т.к. в квадрате - константы, их вычисляем перед циклом один раз. В итерационном цикле изменяемая координата имеет приращение 1, поэтому вместо умножения на квадрат можно использовать сложение с вычисленной вне цикла константой (квадратом). Так сложные операции умножения, деления, вычисления квадратного корня заменяются простыми операциями сложения и вычитания.

Формулы для подсчета d определяются точкой, где 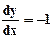. Как ее найти? Можно продифференцировать уравнение эллипса и приравнять результат к -1:

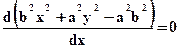
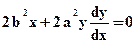
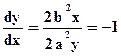
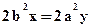
Обычно алгоритм начинается в точке и заканчивается в точке . Движение идет по часовой стрелке. Первоначально 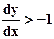. Следовательно, выбор осуществляется между пикселами по вертикали. Затем пикселы выбираются по горизонтали до достижения оси x. Для производится замена вертикального нахождения новой средней точки на горизонтальное. Инкремент для d можно вычислить:

Каждая из полученных точек сразу отображается в остальных трех квадрантах. Пример С-программы - в [ 3 ]. Здесь же приведена более эффективная программа на ассемблере.

В изображении эллипса имеются некоторые проблемы. Когда эллипс мал и для его изображения требуется сравнительно мало пикселов, аппроксимация выглядит как многоугольник (вместо плавной кривой - ломаная). Аналогична ситуация для "тонких" эллипсов с большой разницей между a и b. Выход состоит в переходе к более высокому разрешению (может быть на том же адаптере путем сокращения количества цветов). Другая проблема - вырожденные в прямую эллипсы (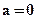или 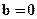). Здесь 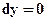или , или , следовательно итерация правильно не заканчивается. В программе перед циклом нужна проверка на вырождение.

Дата добавления: 2014-01-11