Некоторые алгоритмы заполнения областей

Задачи заполнения некоторой замкнутой области также называются задачами закраски. Требуется заполнить внутреннюю часть области пикселами определенного цвета. Рассмотрим 2 класса таких задач: заполнение многоугольников и заполнение области с затравкой.

Для заполнения многоугольника пригоден алгоритм проверки принадлежности точки многоугольнику. Но он не эффективен, т.к. требует перебора всех точек растра. Область перебора можно сократить, вписав многоугольник в прямоугольник со сторонами, параллельными осям, и рассматривая только точки этой области.

Можно сделать другое улучшение. Аналогично тесту на принадлежность точки многоугольнику пересечем прямоугольник горизонталью и зафиксируем точки ее пересечения с много-

угольником (рис. а). Пары

упорядоченных в направле-

нии оси абсцисс точек пере-

сечения дают интервалы, ле-

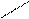
жащие внутри многоугольни-

а) б) в) ка. Теперь вместо одной точ-

ки можно закрасить сразу группу точек, лежащую на некоторой горизонтали внутри многоугольника. Данная схема заполнения называется заполнением в порядке сканирования строк. Алгоритм относится к типу алгоритмов построчного сканирования.

Скорость работы алгоритма можно повысить, если проверять на пересечение со сканирующей прямой не все ребра, а только те, ординаты концов которых лежат по разные стороны этой прямой (рис. б). Используется массив координат концов отрезков, образующих многоугольник, который, как правило, всегда есть.

Для выпуклых многоугольников алгоритм еще проще, т.к. есть всего 2 точки пересечения на каждой растровой прямой (рис. в). Генерируя с помощью алгоритма Брезенхема растровое представление 2 противолежащих ребер для одной и той же ординаты, получаем пикселы, лежащие на границах интервала заполнения.

Задача заполнения области с затравкой формулируется следующим образом. Предполагается, что граница области задана на растровой плоскости набором символов определенного цвета и указаны координаты одной из внутренних точек этой области. Такая точка называется затравочной.

Простейший алгоритм выполняет перебор всех точек и анализ их окрестностей. Возможен анализ в рамках 4- и 8-связности. Для хранения координат точек используется стек. Сначала туда заносятся координаты затравочной точки. Извлечем из стека очередную точку, закрасим ее и исследуем ее 4- или 8-связную окрестность. Если исследуемая точка не лежит на границе фигуры и уже не закрашена, поместим ее в стек. По окончании исследования выберем из стека очередной пиксел, повторим алгоритм. Алгоритм заполняет области любой формы. Но он неэффективен, т.к. один пиксел обрабатывается многократно, стек может неконтролируемо расти.

Более эффективный алгоритм основан на построчном заполнении, что позволяет обрабатывать группы пикселов. Каждую строку можно разделить на интервалы, принадлежащие или не принадлежащие закрашиваемой области. Разделитель - граница области. Если набор пикселов образует связный интервал, принадлежащий внутренней части области, то пикселы над и под этим интервалом либо являются граничными, либо принадлежат внутренней части области. Эти внутренние символы могут служить затравочными для ниже- и вышележащих строк. Целесообразно проверять на возможность использования как затравочных пикселы, лежащие под или над одной из границ найденного интервала.

Пример -rastr\zakras\ line4.cpp из [ 1 ].

#include <conio.h>

#include <graphics.h>

#include <process.h>

#include <stdio.h>

#include <stdlib.h>

int BorderColor = WHITE;

int Color = GREEN;

int LineFill (int x, int y, int dir, int PrevXl, int PrevXr)

{

int xl = x;

int xr = x;

int c;

// Ищем сегмент строки: xl - левая граница, xr - правая граница

do

c = getpixel (--xl, y);

while ((c!= BorderColor) && (c!= Color));

do

c = getpixel (++xr, y);

while ((c!= BorderColor) && (c!= Color));

xl++;

xr--;

// Рисуем линию от xl до xr, y-координата, соответствующая затравочной точке

line (xl, y, xr, y);

getch(); // задержка для просмотра работы алгоритма

// Ищем затравочную точку на след. строке (dir=1) в интервале от xl до xr

for (x = xl; x<= xr; x++)

{

c = getpixel (x, y + dir);

if ((c!= BorderColor) && (c!= Color))

x = LineFill (x, y + dir, dir, xl, xr);

}

for (x = xl; x < PrevXl; x++)

{

c = getpixel (x, y - dir);

if ((c!= BorderColor) && (c!= Color))

x = LineFill (x, y - dir, -dir, xl, xr);

}

for (x = PrevXr; x < xr; x++)

{

c = getpixel (x, y - dir);

if ((c!= BorderColor) && (c!= Color))

x = LineFill (x, y - dir, -dir, xl, xr);

}

return xr;

}

void Fill (int x, int y)

{

LineFill (x, y, 1, x, x);

}

main ()

{

int driver = DETECT;

int mode;

int res;

initgraph (&driver, &mode, "c:\\tcpp\\bgi");

if ((res = graphresult ())!= grOk)

{

printf("\nGraphics error: %s\n", grapherrormsg (res));

exit (1);

}

circle (320, 200, 140);

circle (260, 200, 40);

circle (380, 200, 40);

getch ();

setcolor (Color);

Fill (320, 300);

getch ();

closegraph ();

}

Дата добавления: 2014-01-11