Метод излучательности

Оптимизация трассировки лучей

Метод трассировки лучей требует большого объема вычислений. Причем основная работа заключается в проверке пересечения луча с объектами сцены. В связи с этим простой перебор для многообъектных сцен неэффективен. Требуется сократить количество объектов, для которых проверяется пересечение с лучом.

Особенно долго ищется пересечение с объектами сложной формы. Объект можно поместить внутрь простой фигуры (например, сферы). Если луч не пересекает эту фигуру, то он не пересекает и объект, который исследовать не надо. Пересечение со сферой определить просто, можно использовать, например, аналитический метод (уравнение). Алгебраическое и геометрическое решение этой задачи приведено в [ 1 ] на стр. 122. Там же рассмотрено пересечение луча с плоскостью, выпуклым многоугольником, прямоугольным параллелепипедом. Вспомогательную фигуру пересечет небольшая часть рассматриваемых лучей. Эти лучи проверяются на пересечение со сложной фигурой. Здесь очевиден выигрыш за счет уменьшения количества лучей. Можно описать фигуру вокруг нескольких объектов. При пересечении - аналогичное разбиение группы на подгруппы и т.д. Строится дерево разбиений. Начальная простая фигура содержит всю сцену (аналог дихотомии). Количество проверок на пересечение для данного метода пропорционально O(log n), где n - общее количество объектов.

Ограничивающие фигуры построить не всегда легко. В простейшем случае пространство сцены, вписанное в минимальный исходный параллелепипед, разбивают на равные прямоугольные параллелепипеды. Для каждого из этих блоков составляют список всех объектов, полностью или частично входящих в блок. При проверке пересечения луча берутся только блоки, которые пересекает луч. В блоке объекты сортируются в порядке удаления от начала луча в блоке (аналогично оптимизации путем разбиения картинной плоскости при удалении невидимых линий и поверхностей. Достоинство этого метода оптимизации - простота, следующий блок можно выбирать при помощи алгоритма Брезенхема (блок вдоль луча).

Основной недостаток метода трассировки лучей - неэффективность работы с диффузными поверхностями и зависимость подсчитываемой освещенности от положения наблюдателя. Из-за этого при изменении положения наблюдателя вся сцена перестраивается. Метод излучательности устраняет этот недостаток. В основе метода лежит закон сохранения энергии в замкнутой системе. Все объекты разбиваются на фрагменты, для этих фрагментов составляются уравнения баланса энергии.

Пусть все объекты являются чисто диффузными, т.е. отражают (рассеивают) все равномерно по всем направлениям. Тогда для i -того фрагмента уравнение имеет вид:

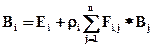i = 1.. n

где 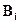- энергия, отбрасываемая i -тым фрагментом сцены,

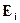- собственная излучательность фрагмента,

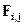- доля энергии j -того фрагмента, попадающая на i -тый фрагмент (коэффициент формы),

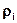- коэффициент отражения.

Если пройти по всем объектам, получим систему линейных алгебраических уравнений.

Из закона сохранения энергии следует, что 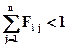для всех i. Система уравнений имеет так называемое сильное диагональное преобладание, для ее решения можно использовать эффективные итерационные методы (типа Гаусса-Зейделя). При этом за небольшое число итераций достигается приемлемое решение.

Для определения цвета фрагмента системы линейных уравнений записываются для каждого из 3 основных цветов. При этом коэффициенты формы определяются только геометрией объектов и от цвета не зависят.

Обычно после определения освещенности каждого фрагмента производят билинейную интерполяцию освещенности по всем объектам (см. закраску методом Гуро), получают плавные естественные переходы цветов. После выбора точки наблюдения объекты проектируются на картинную плоскость и строится изображение.

Наиболее трудоемкий процесс - вычисление коэффициентов формы, которые описывают геометрию сцены. Для этого существуют специальные приемы. Они кратко описаны в [ 1 ].

Дата добавления: 2014-01-11