Политропический процесс. Теплоемкость. Принцип равномерного распределения энергии по степеням свободы и границы его применимости

Лекция 12

Изопроцессы, рассмотренные ранее являются идеализированными. Их нельзя осуществить на практике. К ним можно только приблизиться.

В природе протекают реальные процессы, которые называются политропическими.

Политропическим называется всякий процесс изменения состояния газа, при котором теплоемкость остается постоянной (С = const).

Запишем первое начало термодинамики:

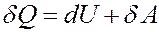(1)

Для политропического процесса получим:

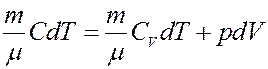(2)

где C – молярная теплоемкость при политропическом процессе. Исключим из (2) температуру. Для этого запишем уравнение Клапейрона-Менделеева и продифференцируем его:

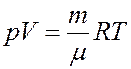
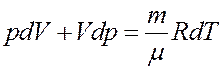
Из последнего уравнения:

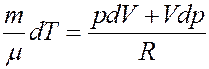(3)

Подставим (3) в (2):

(4)

Преобразуем (4):

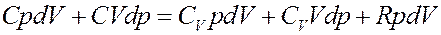(5)

Перегруппируем члены в (5):

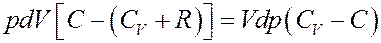(6)

В (6) C_V + R = C_p – молярная теплоемкость при постоянном давлении. Тогда:

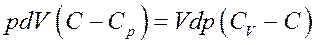
Или:

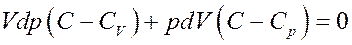(7)

Умножим (7) на

(8)

Обозначим в (8)

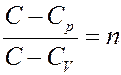
С учетом этого перепишем (8) в виде:

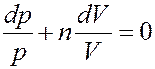(9)

Для данного газа C = const, C_p = const, C_V = const, а значит и n = const. Учитывая это, проинтегрируем (9):

Или:

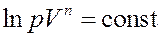
Окончательно:

(10)

Уравнение (10) – это уравнение политропы. Используя уравнение состояния можно получить уравнение политропы в переменных (T,V) (T,p):

(11)

Все изопроцессы являются частными случаями политропического процесса.

Докажем это.

1). Адиабатный процесс: C = 0, тогда

2). Изотермический процесс: С = ∞, тогда:

3). Изобарический процесс: C = C_p, тогда:

4). Изохорический процесс: C = C_V, тогда:

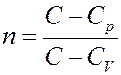
Если С → С_V, то n →±∞. Отсюда следует:

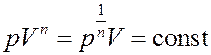
тогда:

,

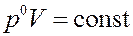или: V = const.

n	Процесс
	Изобарический
	Изотермический
γ	Адиабатный
±∞	Изохорический

Определим работу, которая выполняется при политропическом процессе:

(12)

Запишем уравнение политропы:

(13)

где p ₁, V ₁ – давление и объем газа в начальном состоянии, p ₂, V ₂ – давление и объем газа в конечном состоянии, p, V – давление и объем газа в промежуточном состоянии. Из (13) получим:

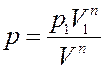(14)

Подставим (14) в (12):

(15)

Рассмотрим случай, когда n ≠ 1, тогда:

С учетом этого из (15) получим:

Или:

(16)

Запишем уравнение Клапейрона-Менделеева:

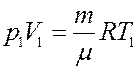
С учетом этого из (16) получим:

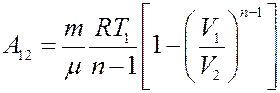(17)

Уравнения (16) и (17) позволяют определить работу для любого политропического процесса, кроме изотермического процесса (n = 1).

Теплоемкость: Теплоемкостью тела или системы (ТДС) называется количество теплоты, необходимое для изменения температуры тела (системы) на 1K.

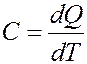
Теплоемкость единицы массы данного вещества называется удельной теплоемкостью, теплоемкость 1 моля – молярной теплоемкостью.

Между удельной c и молярной теплоемкостью C существует простая связь:

где µ - молярная масса данного вещества.

Количество теплоты – функция процесса, поэтому и теплоемкость также функция процесса. То есть теплоемкость одного и того же вещества разная при разных процессах перехода из одного состояния в другое ее нельзя считать характеристикой только самого вещества. Разных процессов бесконечно много, поэтому теплоемкость может принимать значения от - ∞ до +∞.

Особое значение в физике имеет теплоемкость при постоянном объеме C_V и теплоемкость при постоянном давлении C_p.

Молярная теплоемкость при изохорическом процессе (V = const):

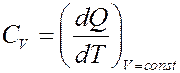
При этом процессе A = pdV = 0. Согласно I началу термодинамики вся теплота, переданная телу (системе) идет на увеличение его внутренней энергии:

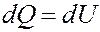
Тогда для 1 моля вещества:

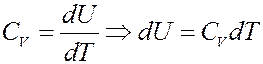
Для газа массой m получим:

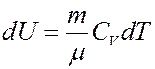(18)

Внутренняя энергия функция параметров состояния, поэтому уравнение (18) определяет приращение внутренней энергии тела (системы) при любом процессе.

Молярная теплоемкость при постоянном давлении:

Тогда для одного моля вещества:

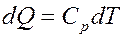
Для газа массой m получим:

(19)

При изобарическом процессе теплота, полученная газом, частично идет на увеличение его внутренней энергии, а частично на работу, выполненную газом. Из (18) и (19) следует, что C_p > C_V.

Запишем первое начало термодинамики для изобарического процесса с учетом (18) и (19):

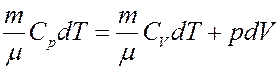(20)

Продифференцируем уравнение Клапейрона-Менделеева, учитывая, что p = const:

(21)

Перепишем (20) с учетом (21):

Из последнего уравнения получим:

(22)

(22) – уравнение Майера.

Классическая теория теплоемкости газов была разработана Больцманом и Максвеллом. В основе этой теории лежит теорема Максвелла-Больцмана о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и на каждую степень свободы молекулы приходится энергия:

.

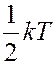Числом степеней свободы механической системы называется число независимых обобщенных координат, которые определяют ее положение и конфигурацию в пространстве.

Положение одноатомной молекулы (материальная точка) полностью определяется тремя ее декартовыми координатами. Следовательно, такая молекула имеет три степени свободы i = 3. Кинетическая энергия одноатомной молекулы:

,

Значит, на одну степень свободы молекулы приходится энергия:

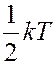
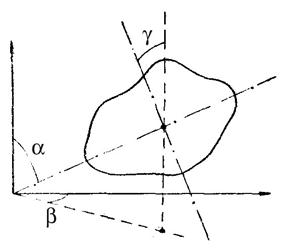
Рис.1. К определению числа степеней свободы

Положение твердого тела в пространстве можно определить, задав три декартовы координаты его центра инерции (масс), два угла, полярный α и азимутальный β, указывающих направление какой-либо оси, связанной с телом и проходящей через его центр масс, а также углом γ, определяющим направление другой связанной с телом оси, перпендикулярной первой и проходящей через центр масс.

Таким образом, твердое тело имеет шесть степеней свободы. Изменение координат центра масс (x, y, z) при неизменных углах α, β и γ обусловлено поступательным движением твердого тела. Поэтому эти степени свободы называются поступательными. Изменение любого из углов α, β и γ при неизменном положении центра масс (x, y, z) обусловлено вращением тела. Эти степени свободы называются вращательными.

Следовательно, из шести степеней свободы абсолютно твердого тела три степени свободы являются поступательными и три вращательными.

Система из N материальных точек (молекул) имеет 3 N степеней свободы, потому что положение каждой из N точек (молекул) должно быть задано тремя координатами (x, y, z).

Любая жесткая связь, которая устанавливается между двумя точками и обеспечивает их неизменное взаимное расположение, уменьшает число степеней свободы на единицу. Например, двухатомная молекула, которая состоит из двух жестко связанных атомов, имеет пять степеней свободы рис.2 (число степеней свободы для двух несвязанных атомов равно 3*2 = 6).

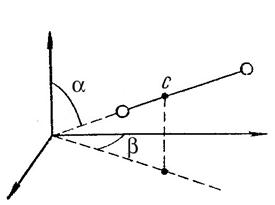
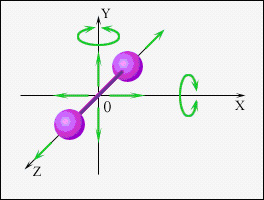
Рис.2. Число степеней свободы двухатомной молекулы.

Положение двухатомной молекулы можно определить тремя координатами центра масс (x, y, z) и двумя углами α и β, которые определяют направление оси молекулы в пространстве. Отсюда следует, что три степени свободы будут поступательными, а две - вращательными. Вращательные степени свободы соответствуют вращению вокруг двух взаимно перпендикулярных осей x и y. Вращение вокруг оси z, проходящей через ось молекулы, не изменяет положение и конфигурацию молекулы в пространстве (рис.2).

Трехатомная молекула имеет шесть степеней свободы: три поступательных и три вращательных (рис.3).

Рис.3. Число степеней свободы трехатомной молекулы.

Если связь между атомами не жесткая, а упругая необходимо учитывать колебательные степени свободы. На каждую колебательную степень свободы приходится 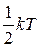в виде кинетической энергии и 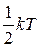в виде потенциальной энергии.

Таким образом, число степеней свободы может быть рассчитано как сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы следующим образом:

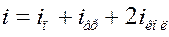
Если число степеней свободы i, то средняя энергия молекулы:

Внутренняя энергия 1 моля такого газа:

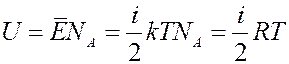
Тогда молярная теплоемкость при V = const:

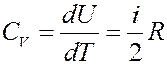(23)

С учетом (23) молярная теплоемкость при p = const:

(24)

Отношение теплоемкостей:

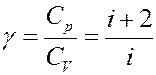(25)

Если:

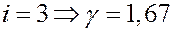
Численные значения C_p и C_V, а также и γ совпадают с экспериментальными данными, полученными при комнатных температурах для одноатомных и двухатомных газов. Для многоатомных молекул экспериментальные данные значительно отличаются от теоретических. Согласно классической теории теплоемкость не зависит от температуры. Эксперименты при низких и высоких температурах показывают, что теплоемкость зависит от температуры.

При низких температурах теплоемкость всех веществ меньше, чем при высоких. Эти отступления от классической теории свидетельствуют о неточности теоремы о равномерном распределении энергии по степеням свободы, которая лежит в основе классической теории.

Молекулы состоят из атомов, которые в свою очередь складываются из еще меньших элементарных частиц. Движение элементарных частиц не подчиняется законам классической механики. В многоатомных молекулах надо учитывать внутриатомные процессы, которые подчиняются законам квантовой механики. Полное объяснение всех экспериментальных результатов дает квантовая теория теплоемкости.

Дата добавления: 2014-01-11