Steps for solving a separate first order differential equations

A separable fist order differential equation.

Definition 3.1. A first order differential equation is separable if it can be put in the form

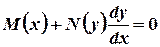
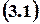
or in the equivalent differential form

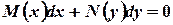
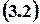
When we write the equation by this way we say that we have separated the variables.

1. If differential equation is given in the form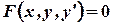, than we make a substitution 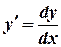and multiply both parts of equations by .

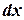2. Separate the variables and write the equation in the form .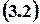

3. Integrate 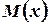with respect to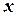, 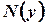- with respect to, and right-hand side of equation - with respect to any variable.

Example 3.1. Find the general integral, the general solution and the particular solution satisfying such initial conditions

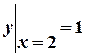
of the differential equation

.

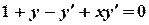Solution. Make substitution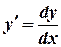

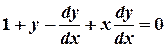
Multiply by 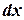and separate variables

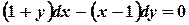
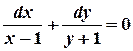
Integrate both parts of the equation

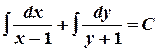
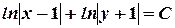
We have found the general integral of the differential equation.

For finding the general solution we need to solve last equation with respect to

Because 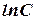is also arbitrary constant we will make substitution.

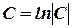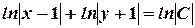
By properties of the logarithms

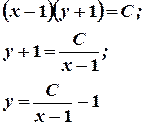
We have found the general solution of the differential equation.

Let to find C. Using the initial condition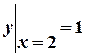, we obtain

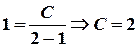
Substituting 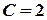into the general solution we shall get

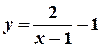
This is the particular solution of the given differential equation.

Example #3.1 (The problem of the change in population over the time.)

Solution. From the an example of §1 we have

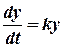, initial condition.

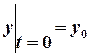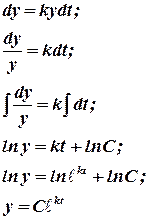
Using initial condition we will find C

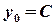, then

.

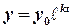From last equation we can make the conclusion:

1) when 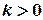then the population increases;

2) when 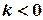then the population decreases;

3) when 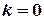then the population remains constant over the time.

Дата добавления: 2014-01-11