
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Expansion of the proper rational fraction into partial fractions
|
|
|
|
Integration of the partial rational fractions.
Example 7.2.
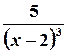 ;
; 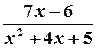 ;
;  - partial fractions.
- partial fractions.
I. 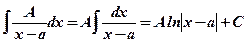 ;
;
II. 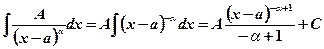 , where
, where 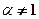
.
III. 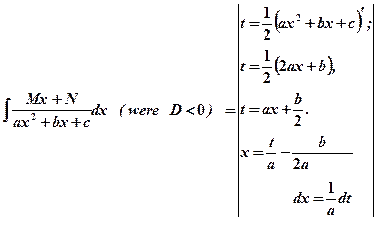 .
.
As a result of this substitution considered integral leads to the sum of table integrals
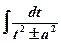 and
and 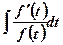 .
.
IV. 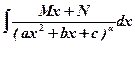
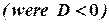 .
.
Integrals in the form IV can be evaluated by substitution which was used for integrals in the form III.
Let  - proper irreducible rational fraction. Consider two cases:
- proper irreducible rational fraction. Consider two cases:
Case 1. 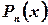 has only real roots
has only real roots 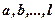 multiplicity of
multiplicity of 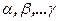 , so
, so
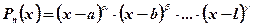 then
then
 =
=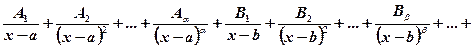
+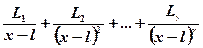 (7.1), were
(7.1), were 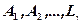 - coefficients must be found.
- coefficients must be found.
Case 2. 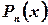 except real roots
except real roots 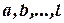 multiplicity of
multiplicity of 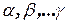 , has roots which are solutions of equation
, has roots which are solutions of equation 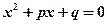 when
when 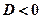 , so
, so
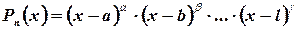
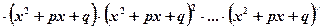 then
then
 =
=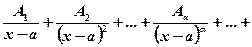
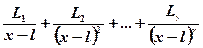 +
+
+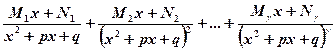 (7.2) were
(7.2) were 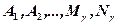 - coefficients must be found.
- coefficients must be found.
Example 7.3. Decompose rational fraction into the sum of partial fractions.
a) 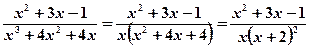
Solution:
Using expansion (7.1) we have
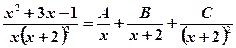 , where
, where 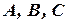 - unknown coefficients.
- unknown coefficients.
To find unknown coefficients we reduce the fractions of the right side of last equation to the common denominator and equate numerators of both sides of the equation.
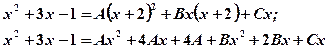
Equate the coefficient of corresponding powers of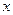 , and solve the resulting equations for the unknown coefficients
, and solve the resulting equations for the unknown coefficients
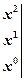
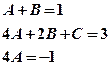
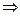
 ;
;
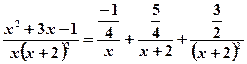 .
.

|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 467; Нарушение авторских прав?; Мы поможем в написании вашей работы!