Правило Байеса

Пусть имеется группа событий 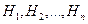(классов, к которым относятся входные сообщения), обладающая следую­щими свойствами:

1) все события попарно несовместны: ;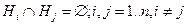

2) их объединение образует пространство элементарных исходов W:

.

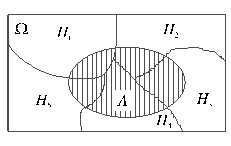
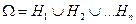В этом случае будем говорить, что H ₁, H ₂,..., H_n образуют полную группу событий. Такие события иногда называют гипотезами.

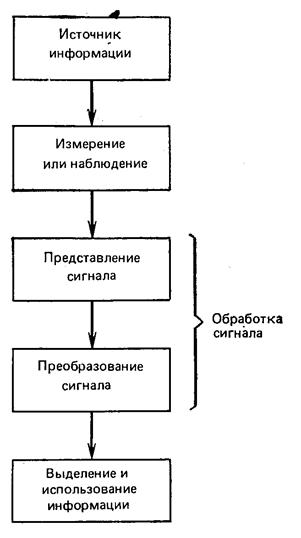
Рис. 7.2. Декодирование сигнала и выделение информации.

Пусть 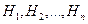- полная группа событий и 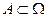– некоторое событие. Тогда по формуле Байеса исчисляется вероятность реализации гипотезы 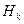при условии, что событие А произошло. Формула Байеса, полученная Т. Байесом в 1763 году, позволяет вычислить апостериорные вероятности событий через априорные вероятности и функции правдоподобия.

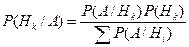
Здесь А – конкретное наблюдение (измерение). Формулу Байеса еще называют формулой вероятности гипотез. Будем считать, что у нас достаточно данных для определения вероятности принадлежности объекта каждому из классов. Вероятность 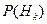называют априорной вероятностью гипотезы 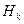, а вероятность 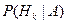– апостериорной вероятностью, поскольку задает распределение индекса класса после эксперимента (a posteriori – т.е. после того, как измерение было произведено). Также будем считать, что известны функции распределения вектора признаков для каждого класса 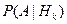. Они называются функциями правдоподобия A по отношению к H _k. Если априорные вероятности и функции правдоподобия неизвестны, то их можно оценить методами математической статистики на множестве прецедентов. Байесовский подход исходит из статистической природы наблюдений. За основу берется предположение о существовании вероятностной меры на пространстве образов, которая либо известна, либо может быть оценена. Цель состоит в разработке такого классификатора, который будет правильно определять наиболее вероятный класс для пробного образа. Тогда задача состоит в определении "наиболее вероятного" класса.

Если априорные вероятности и функции правдоподобия неизвестны, то их можно оценить методами математической статистики на множестве прецедентов. Например, 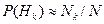, где 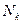– число прецедентов из 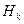. N – общее число прецедентов. 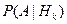может быть приближено гистограммой распределения вектора признаков для прецедентов из класса .

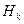Рассмотрим случай двух классов 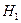и 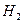. Естественно выбрать решающее правило таким образом: объект относим к тому классу, для которого апостериорная вероятность выше. Такое правило классификации по максимуму апостериорной вероятности называется Байесовским: если 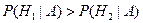, то А классифицируется в 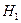, иначе в 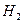. Таким образом, для Байесовского решающего правила необходимо получить апостериорные вероятности 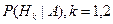. Это можно сделать с помощью формулы Байеса.

Итак, Байесовский подход к статистическим задачам основывается на предположении о существовании некоторого распределения вероятностей для каждого параметра. Недостатком этого метода является необходимость постулирования как существования априорного распределения для неизвестного параметра, так и знание его формы.

Дата добавления: 2014-01-11