Процедура принятия решения. Динамическое программирование.Процедура динамического программирования сводится к нелинейному нормированию во времени двух развертывающихся во времени речевых

Динамическое программирование. Процедура динамического программирования сводится к нелинейному нормированию во времени двух развертывающихся во времени речевых процессов - входного и эталонного речевых событий. Впервые процедура динамического программирования была предложена для распознавания изолированных слов в работах [Величко, Винцюк, Слуцкер].

Он был также модифицирован для распознавания слитной речи, но в силу большой вычислительной емкости этот метод в реальных системах широкого распространения не получил.

При обучении некоторым образом формируются эталонные образы слов в виде последовательности векторов параметров речевого сигнала 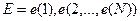. Каждый вектор 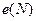описывает речевой сигнал на интервале наблюдения, длительность которого обычно выбирается равной среднему периоду основного тона, равному 15 мсек.

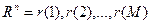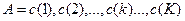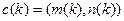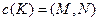При распознавании последовательность входных векторов сравнивается с эталонной последовательностью на плоскости (Рис. 14), вдоль осей которой откладываются входная R и эталонная E последовательности. Последовательность точек , где , , и 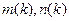– точки на осях, соответствующие сравниваемым векторам параметров последовательностей, задает функцию деформации, определяющую временное согласование сравниваемых образов.

В качестве меры расхождения между векторами признаков 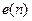и 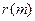вводится расстояние между ними, например,

,

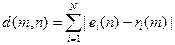где 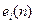и 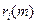– компоненты векторов 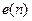и 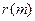, соответственно.

Взвешенная сумма расстояний для функции деформации:

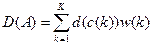, (7.16)

где 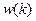– весовой коэффициент, который определяется по формулам:

- для симметричной формы процедуры:

,

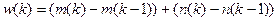- для ассиметричной формы:

,

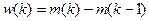или:

.

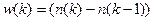Значения 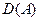служат оценкой качества функции деформации. Минимальные значения достигаются при оптимальном согласовании временных расхождений между образами. Компенсируя в выражении для 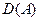влияние числа точек на меру, можно написать функциональное уравнение, решение которого определяет нормализованное по времени расстояние между образами,

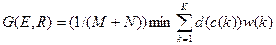. (7.17)

На функцию деформации накладываются ограничения по монотонности:

,

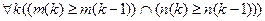по непрерывности:

,

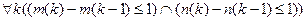и на область допустимых значений (Рис. 16):

,

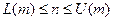где 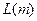и – границы изменения значения n для данного значения m.

Иногда вводится ограничение на наклон функции деформации. Если точка 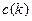продвигается вперед в направлении оси n (или m) последовательно t раз, то не допускается, чтобы 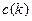перемещалось дальше в том же направлении, не сделав по крайней мере p шагов в направлении диагонали.

Если ограничения на наклон слишком жесткие, временная нормализация малоэффективна, если ограничения слишком мягкие, то плохо различаются образы, относящиеся к разным классам. Экспериментально показано, что наилучшие результаты дает процедура с ограничением .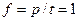

Алгоритм процедуры динамического программирования при этих условиях можно представить следующим образом:

начальное условие

;

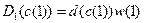функциональное уравнение

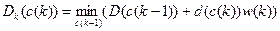; (7.17)

окончательное решение

.

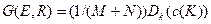Предполагается, что 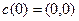. Соответственно 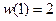. Для 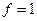уравнение (7.17) выглядит следующим образом:

.

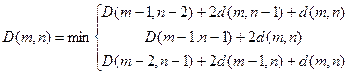При распознавании реализация контрольного слова сравнивается с каждым эталоном, в результате чего формируется последовательность нормализованных расстояний: 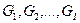. Решение принимается по правилу:

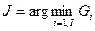
Иногда процедура временной нормализации осуществляется от конца слова к его началу.

Скрытые Марковские модели. Используем методы статистического моделирования для интерпретации речевых событий, поступающих на вход системы.

Для эффективного учета временных вариаций речевого сигнала используем подход на основе скрытых Марковских моделей (СММ). Для этого предположим, что речевой сигнал, являющийся нестационарным процессом, можно представить в виде кусочно-стационарного процесса. В этом случае речевому высказыванию, представленному последовательностью векторов признаков Y, можно поставить в соответствие последовательность дискретных стационарных состояний:

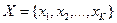, (7.18)

где 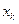– состояние процесса в момент времени n.

На входе системы, использующей статистические методы моделирования, имеется последовательность векторов признаков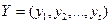, полученных в результате первичной обработки (например, речевой волны). Для выработки статистических гипотез берется некоторое множество классов 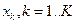, к которым эти гипотезы должны быть отнесены. В общем случае задача классификации может рассматриваться как статистическая задача распознавания образов, что позволяет построить оптимальный классификатор на основе критерия максимума апостериорной вероятности:

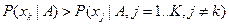, (7.19)

где – 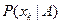вероятность принадлежности заданного образа классу .

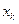Пусть 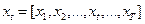– множество состояний модели, из которых формируются модели речевых высказываний, следовательно, 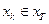и состояние модели 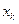в момент времени t можно обозначить как .

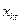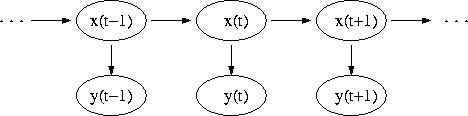
Рис. 7.11.

Введенная таким образом модель описывает дважды стохастический процесс: последовательность состояний модели, моделирующих временную структуру речи, является выборочной функцией некоторого случайного процесса; наблюдаемый процесс, определяемый локально-стационарными свойствами речевого сигнала, также является случайным процессом. Модель является скрытой, так как основной процесс (последовательность состояний) непосредственно не наблюдается. Основной процесс перехода между стационарными состояниями является Марковским, так как статистические данные текущего состояния зависят только от его собственных характеристик и характеристик предыдущего состояния.

Для конечных стохастических процессов знание исходов уже наблюдавшихся экспериментов не влияет на прогноз относительно последующего эксперимента. Для Марковских процессов знание непосредственно предшествующего исхода влияет на этот прогноз.

Марковские процессы с дискретным временем называются Марковскими цепями. Конечной Марковской цепью называется конечный стохастический процесс такой, что для любого высказывания 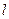, истинность которого зависит лишь от исходов экспериментов до n-го:

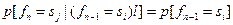(7.20)

(предполагается, что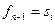и 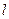совместимы).

Пусть Марковская цепь первого порядка из K-состояний задается [9] матрицей переходных вероятностей 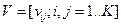, и вектором начальных вероятностей 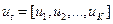. Очевидно,

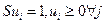(7.21)

и

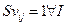, (7.22)

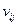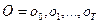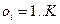так как есть вероятность перехода из состояния i в состояние j, если текущим состоянием является i. Для любой последовательности с конечным числом состояний , где , вероятность генерации O Марковской цепью может быть вычислена как:

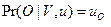
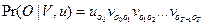. (7.23)

Предположим, что 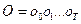не может наблюдаться непосредственно. Вместо нее мы наблюдаем стохастический процесс 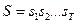, генерируемый подлежащей последовательностью состояний 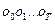. Каждое состояние проявляет себя через функцию плотности вероятности 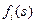. Используем обозначение 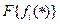для множества таких функций. Плотность вероятности наблюдения 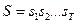, порожденного данной последовательностью состояний O, генерированных Марковской цепью с матрицей переходных вероятностей V и начальной вероятностью u, есть, таким образом:

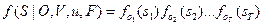. (7.24)

Каждое 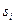здесь - вектор без неопределенности. Отсюда следует, что плотность вероятности наблюдения S при данных V и u есть:

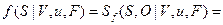
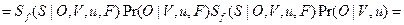
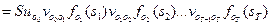. (7.25)

Стохастический процесс S характеризуется плотностью 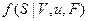и множеством функций плотности вероятности F, которые предполагаются известными и независимыми от Марковской цепи. Триада 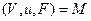называется далее (скрытой) Марковской моделью, а условная плотность для стохастического процесса S может быть записана как .

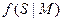Далее рассмотрим применение скрытых Марковских моделей для решения задачи распознавания (временных) образов. Она вновь рассматривается как задача классификации. Необходимо распознать последовательность, о которой известно, что она принадлежит к некоторому словарю W, состоящему из I слов W(1), W(2),..., W(I). Каждое слово W(i) представлено моделью . При этом дается последовательность наблюдений 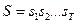. Тогда мы применяем правило максимального правдоподобия и классифицируем S как слово W(i) тогда и только тогда,

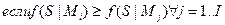. (7.26)

Указанная проблема вновь разбивается на две части: оценка 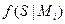и нахождение модели M, максимизирующей правдоподобие данного наблюдения S. Первая задача эффективно решается, например, с помощью оценочного алгоритма Baum [7] для некоторого класса скрытых Марковских моделей, включая таковые с Гауссовскими авторегрессионными плотностями вероятностей. Вторая задача эффективно решается с помощью алгоритмов динамического программирования (алгоритм Витерби) [8].

Дата добавления: 2014-01-11