
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Figure 8.1
|
|
|
|
The area under the curve.
Suppose 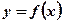 is nonnegative, continuous throughout
is nonnegative, continuous throughout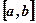 . We want to define the area of the region enclosed by the graph of the function
. We want to define the area of the region enclosed by the graph of the function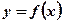 , the
, the 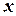 -axis and the vertical lines
-axis and the vertical lines 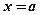 and
and 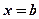 . We call this area the area under the curve
. We call this area the area under the curve 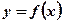 from
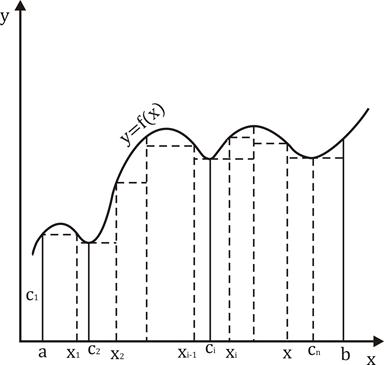
from 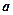 to
to 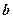 .
.
We partition 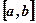 into
into 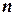 subintervals of the length
subintervals of the length 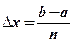 by choosing the points
by choosing the points 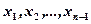 such that
such that
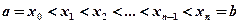 .
.
The vertical lines through the points 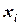 divide the region into vertical strips. We approximate each strip with an inscribed rectangle with base
divide the region into vertical strips. We approximate each strip with an inscribed rectangle with base 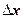 and the height which is equal to the minimum value of the function on the rectangle base
and the height which is equal to the minimum value of the function on the rectangle base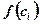 . So, the area of
. So, the area of 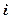 -th rectangle equals
-th rectangle equals 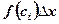 and the sum of the areas of the rectangles will be
and the sum of the areas of the rectangles will be
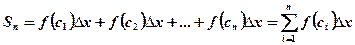
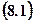
This formula approximates the area under the curve 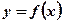 from
from 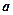 to
to 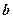 .
.
The area approximation given by formula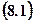 may not be particularly good if the number of the rectangles is small. To increase approximation we can by approaching the number
may not be particularly good if the number of the rectangles is small. To increase approximation we can by approaching the number 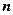 to the infinity
to the infinity
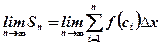
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 492; Нарушение авторских прав?; Мы поможем в написании вашей работы!