
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы распределения носителей в зонах полупроводников
|
|
|
|
Зонная структура полупроводников

Зонные структуры полупроводников:
(a) – собственный полупроводник при Т ≠ 0,
(б) – электронный полупроводник при Т = 0,
(в) – дырочный полупроводник при Т = 0.
Энергетические уровни распределены по высоте разрешенной зоны неравномерно: плотность их меняется от границы в глубь зоны. Таким образом, каждому уровню с энергией W соответствует определенная плотность P(W), то есть число уровней, отнесенное к единице энергии и единице объема твердого тела. Вблизи “дна” и “потолка” каждой из разрешенных зон плотность плотность уровней P (φ) с нормированной энергией (в вольтах) φ = W/e (для узких интервалов энергии d φ) выражается следующей формулой:
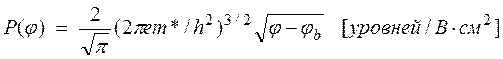
где φb – граница зоны, m * - эффективная масса. Энергия отсчитывается от граничного уровня φb внутрь зоны.
Вероятность нахождения электрона на том или ином уровне дается распределением Ферми-Дирака:
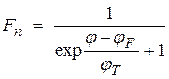
“Темпер. потенциал” φT = kT/e ≈ T/11600, φT (300K) ≈ 0,025 В.

Плотность уровней энергии, функция вероятности и концентрация носителей в собственном полупроводнике.
φF – уровень Фе рми, который в невырожденных полупроводниках всегда лежит в запрещенной зоне.
При T ≠ 0 для зон проводимости и валентной зоны (т.е. для областей энергий, достаточно отличных от энергии Ферми φF) распределение Ф-Д переходит в распределение Максвелла - Бльцмана (т.к. ׀ φ - φF ׀ >> φT):
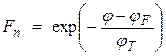 ,
, 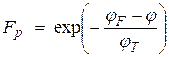
Концентрация свободных электронов в зоне проводимости:
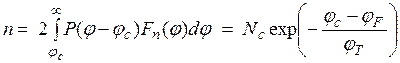 ,
,
где 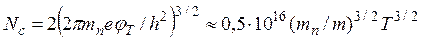 - эфф. плотность состояний (на 1 см3) в зоне проводимости. При получении этой формулы было использовано соотношение:
- эфф. плотность состояний (на 1 см3) в зоне проводимости. При получении этой формулы было использовано соотношение:
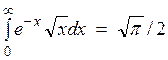
Концентрация свободных дырок в валентной зоне:
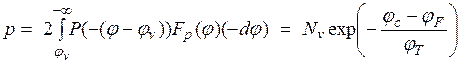 ,
,
где 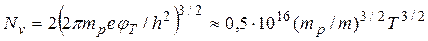 - эфф. плотность состояний (на 1 см3) в валентной зоне.
- эфф. плотность состояний (на 1 см3) в валентной зоне.
 ,
, 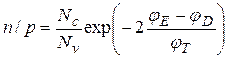 , где
, где 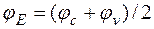
Уровень Ферми является функцией концентраций носителей.
Задача определения уровня Ферми (обр. задача) определяется интегралом:
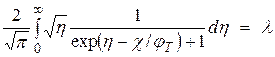 , (*)
, (*)
где χ – хим. потенциал.
В случае электронов 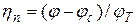 ,
,  ,
,  .
.
В случае дырок 
 ,
, 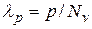 ,.
,.
 или
или 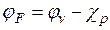 ,
,
φF – эл.-хим. потенциал, характеризующий и диффузию, и дрейф частиц. Поэтому в условиях равновесия φF = const.
1. Случай χ < 0, ׀ χ ׀ >> φT (невырожденные полупроводники: λ < 1).
В этом случае уравнение (*) существенно упрощается:
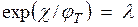 ,
,
Отсюда получаем следующие выражения:
 ,
, 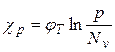
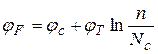 или
или 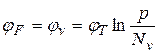 .
.
2. Случай χ > 0, ׀ χ ׀ >> φT (вырожденные п/п или полуметаллы: λ > 1).
В этом случае, аппроксимируя функцию  ступенчатой функцией, которая равна 1 при
ступенчатой функцией, которая равна 1 при 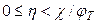 и равна 0 при
и равна 0 при 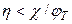 , из уравнения (*) получаем выражение:
, из уравнения (*) получаем выражение:
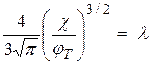 .
.
Отсюда следует, что
 ;
; 
Эти выражения справедливы при λ >> 1 (практически при λ > 3) в силу того, что рассматривается случай ׀ χ ׀ >> φT. Полупроводники, у которых концентрация свободных носителей существенно превышает эффективную плотность состояний в разрешенной зоне, называют вырожденными или полуметаллами. Для них распределение максвелла – Больцмана недействительно и в случае сильного вырождения заменяется ступенчатой функцией: 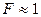 при
при 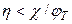 и
и 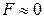 при
при 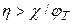 . Критерии вырождения:
. Критерии вырождения: 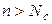 и соответственно
и соответственно  .
.
Потенциал Ферми для вырожденных полупроводников лежит внутри соответствующей разрешено зщоны, поскольку хим. потенциалы χn и χp положительны.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 878; Нарушение авторских прав?; Мы поможем в написании вашей работы!