Создание матриц и базовые матричные операции

ИСПОЛЬЗОВАНИЕ МАТРИЦ В MATLAB.

Базовой структурой данных в MATLAB является матрица (matrix): двухмернaя, имеющая прямоугольную форму структура данных, в которой хранится набор элементов данных в простом и легко доступном формате. Эти элементы данных могут быть числами, символами, логическими единицами true или false, или даже другими типами структур данных MATLAB. В MATLAB используются двухмерные матрицы для хранения отдельных чисел, а также, линейных последовательностей данных. В этих случаях размерности 1×1 и 1×n, соответственно, где n – длина числовой последовательности. MATLAB также поддерживает структуры данных, которые имеют больше чем два измерения. В MATLAB эти структуры данных имеют название arrays (массивы). MATLAB является вычислительной средой, основой которой является матрица. Все вводимы в MATLAB данные хранятся в форме матрицы или многомерного массива.

Матрица – это двух мерный массив вещественных или комплексных чисел. В MATLAB имеется ряд функций, которые позволяют создавать различные типы матриц. Простейший способ создания матрицы в MATLAB – использовать оператор констора матрицы, []. Этот оператор создает строку в матрице при вводе элементов (показаны ниже как E) в скобках. Каждый элемент необходимо отделять запятой или пробелом:

row = [E1, E2,..., Em] row = [E1 E2... Em]

Например, для того, чтобы создать матрицу из пяти элементов, напечатайте

A = [12 62 93 -8 22];

Для того, чтобы начать новую строку, надо закончить текущую точкой с запятой:

A = [row1; row2;...; rown]

В этом примере вводится матрица, состоящая из 3-х строк и 5-и столбцов (3×5) чисел. Все строки должны иметь одинаковое число элементов,

A = [12 62 93 -8 22; 16 2 87 43 91; -4 17 -72 95 6]

A =

12 62 93 -8 22

16 2 87 43 91

-4 17 -72 95 6

Этот оператор констора матрицы может создавать только двухмерные матрицы (включая 0×0, 1×1, 1×n,).

Специализированные матричные функции.

Функция	Описание
ones	Создает матрицу или массив, состоящий из всех единиц
zeros	Создает матрицу или массив, состоящий из всех нулей
eye	Создает матрицу с единицами на диагонали и остальными нулями
аccumarray	Распределяет элементы входной матрицы в соответствии с заданным положением в выходной матрице
diag	Преобразует вектор в диагональную матрицу
magic	Создает квадратную матрицу, в которой сумма элементов строк, или элементов столбцов, или элементов главных диагоналей одинакова
rand	Создает матрицу или массив случайных чисел имеющих равномерное распределнием
randn	Создает матрицу или массив случайных чисел или случайных массивов имеющих нормальное распределнием
randperm	Создает вектор (1-на-n матрицу) содержащий случайное размещение заданного числа целых

Например, для создания волшебной квадратной матрицы 5×5 воспользумся функцией magic,

A = magic(5)

Конкатенация (объединение) матриц.

Матричная конкатенация – это объединение одной или большего числа матриц, для получения новой матрицы. Скобки [] используются не только как конструктор матрицы, но также как оператор конкатенации. Результатом выражения C = [A B] является конкатенация матриц A и B по горизонтали. Результатом выражения C = [A; B] является конкатенация матриц A и B по вертикали. This example constructs a new matrix C by concatenating matrices A and B in a vertical direction:

A = ones(2, 5) * 6; % матрица 2×5 все элементы которой равны 6

B = rand(3, 5); % матрица 3×5 состоящая из случайных чисел

C = [A; B] % конкатенация матриц A и B по вертикали

Функции матричной конкатенации

Функция	Описание
cat	Конкатенация матриц вдоль заданного направления
horzcat	Конкатенация матриц по горизонтали
vertcat	Конкатенация матриц по вертикали
repmat	Конкатенация матриц по горизонтали и по вертикали
blkdiag	Создания блочной диагональной матрицы из существующих матриц

Генерирование числовых последовательностей, оператор двоеточие (:).

Оператор двоеточие (first:last) генерирует матрицу 1×n (или вектор) последовательных чисел от первого числа до последнего. По умолчанию получаем последовательность чисел, увеличивающихся на единицу, каждое последующее на 1 больше предыдущего.

A = 10: 15

A =

10 11 12 13 14 15

Последовательность чисел не обязательно должна состоять из целых положительных. Она может содержать отрицательные числа, а также дроби:

A = -2.5: 2.5

A =

-2.5000 -1.5000 -0.5000 0.5000 1.5000 2.5000

Для генерирования числовых последовательностей с шагом, отличным от 1, оператор двоеточие может использоваться со указанием величины приращения элементов (first:step:last). Величина step указывает шаг приращения (уменьшения, если step является отрицательным числом) элементов последовательности чисел. Например,

A = 10: 5: 50

A =

10 15 20 25 30 35 40 45 50

Шаг может быть дробным или отрицательным числом,

A = 3: 0.2: 3.8

A =

3.0000 3.2000 3.4000 3.6000 3.8000

A = 9:-1: 1

A =

9 8 7 6 5 4 3 2 1

Индексация матриц.

Для доступа к отдельному элементу матрицы задайтеномерстроки и номерстолбца используя следующу запись A(n, m), где A – матричная переменная. Номерстолбца всегда указывается первым, а номерстолбца – втрым, например,

A = magic(4)

A =

16 2 3 13

5 11 10 8

9 7 6 12

4 14 15 1

для доступа к элементу в 4-й строке, 2-й колонке напечатайте

A(4, 2)

ans =

Для массивов, которые имет размерность большую двух, необходимо задавать дополнительные индексы, которые следуют за индексами строк и столбцов.

Линейная индексация матриц. Вы можете обращаться к элементу матрицы используя единственный индекс, A(k). MATLAB хранит матрицы и массивы не в той форме, в которой они появляются в командном окне, а как единый столбец элементов. Этот единый столбец составлен из столбцов матрицы, каждый столбц присоединяется к предыдущему. Так, матрица A

A = [2 6 9; 4 2 8; 3 5 1]

A =

2 6 9

4 2 8

3 5 1

в действительности хранится в памяти как последовательность

2, 4, 3, 6, 2, 5, 9, 8, 1

Элемент с строке 3, столбец 2 матрицы A (значение = 5) может быть идентифицирован как элемент 6 в действительной хранимой последовательности. Для доступа к этому элементу, есть возможность использовать стандартный синтаксис A(3,2), или есть возможность применить A(6), относящуюся к линейной индексации.

Обращение к последовательности элементов. Для матрицы A размерности 4×4, сумму элементов 4-го столбца можно вычислить набрав

A = magic(4);

A(1,4) + A(2,4) + A(3,4) + A(4,4)

Можно уменьшить размер выражения используя оператор двоеточие. Индексные выражения, включающие двоеточия, обращаются к последовательности элементов матрицы. Выражение,

A(1:m, n)

обращается к элементам в строках с 1-й по m-ю, n-го столбца матрицы A. Используя эту запись, можно вычислить сумму элементов 4-го столбца матрицы A более компактно:

sum(A(1:4, 4))

Обращение к элементам, которые не следуют друг за другом. Для этого используйте оператор двоеточия с величиной шага. Выражение m: 3: n означает обращение к каждому третьему элементу матрицы. При линейной индексации имеем:

B = A;

B(1:3:16) = -10

B =

-10 2 3 -10

5 11 -10 8

9 -10 6 12

-10 14 15 -10

MATLAB поддерживает тип индексации массивом, при которой один массив используется как индекс в другом массиве. Этот тип индексации может быть основан на задании в массиве индексов либо номеров, либо размещения элементов. В приведенном ниже примере массив B состоит из индексов 1, 3, 6, 7, и 10 массива A. В этом случае, числовые значения элементов массива B соответствуют положению элементов в массиве A:

A = 5:5:50

A =

5 10 15 20 25 30 35 40 45 50

B = [1 3 6 7 10];

A(B)

ans =

5 15 30 35 50

Ключевое слово end (конец). MATLAB предоставляет ключевое слово end для доступа к последнему элементу массива. В предыдущем примере можно использовать запись

B(1:3:end) = -10

Описание всех элементов строки или столбца. Двоеточие само по себе относится ко всем элементам строки или столбца матрицы. Используя следующую запись может быть вычислена сумма элементов во 2-м столбце волшебной квадратной 4×4 матрицы A:

sum(A(:, 2))

ans =

Используя двоеточие в линейной индексации можно обратиться ко всем элементам всей матрицы.

A(:)

ans =

.

.

.

Получение информации о матрице.

Функции, возвращающие информации о форме матрицы.

Функция	Описание
length	Возвращает величину самой длинной размерности
ndims	Возвращает число размерностей
numel	Возвращает число элементов
size	Возвращает длину каждой размерности

Изменение размерности и формы матриц.

Способы увеличения размерности матрицы.

• Конкатенация новых элементов

• Размещение элементов за границами матрицы

Конкатенация наиболее подходит, если необходимо добавить к матрице новые элемнты или блоки, совместимые по размерности с исходной матрицей.

Для добавления одного или большего числа элементов к матрице, которые не совместимы по размерности с исходной матрицей, часто можно разместить новые элементы за границами исходной матрицы. MATLAB автоматически дополнит матрицу нулями, для того, чтобы она была прямоугольной.

Пример. Дана матрица 3×5,

A = [ 10 20 30 40 50;...

60 70 80 90 100;...

110 120 130 140 150];

ее необходимо дополнить 4-й строкой. Разместим новый элемент в 1-м столбце не существующей 4-й строки исходной матрицы. MATLAB расширит матрицу A добавлением новой 4-й строки, заполнив нулями колонки со 2-й по 5-ю.

A(4,1) =0

A =

10 20 30 40 50

60 70 80 90 100

110 120 130 140 150

0 0 0 0 0

Размерность матрицы может быть уменьшена за счет удаления строк и столбцов из матрицы присваиванием удаляемым строкам и столбцам значения пустого массива.

Пример. Дана матрица 4×4,

A = magic(4)

A =

16 2 3 13

5 11 10 8

9 7 6 12

4 14 15 1

из нее необходимо удалить 2-й столбец,

A(:, 2) = []

результат:

A =

16 3 13

5 10 8

9 6 12

4 15 1

Для удаления единственного элемента или последовательности элементов может быть использована линейная индексация. При этом результатом будет преобразование оставшихся элементов в вектор-строку,

A(2: 2: 10) = []

в результате получим:

A =

16 9 3 6 13 12 1

Функции, изменяющие форму матрицы

Функция	Описание
reshape	Изменяет форму матрицы
rot90	Вращает матрицу на 90 градусов
fliplr	Поворачивает матрицу относительно вертикальной оси
flipud	Поворачивает матрицу относительно горизонтальной
flipdim	Поворачивает матрицу относительно заданного направления
transpose	Поворачивает матрицу относительно ее главной диагонали, заменяя вектора-строки на вектора-столбцы, и наоборот
ctranspose	Транспонирует матрицу и заменяет каждый элемент комплексно-сопряженным

Примеры применения функций, изменяющих форму матрицы.

Используя матрицу А, имеющую размерность 3×4 построить матрицу В размерности 2×6:

A = [1 4 7 10; 2 5 8 11; 3 6 9 12]

A =

1 4 7 10

2 5 8 11

3 6 9 12

B = reshape(A, 2, 6)

B =

1 3 5 7 9 11

2 4 6 8 10 12

Для транспонирования матрицы можно использовать как функцию transpose, так и оператор (.')s:

B = A.'

B =

1 2 3

4 5 6

7 8 9

10 11 12

Скаляры. Скалярная величина – это любое отдельное вещественное или комплексное число, которое представлено вMATLAB как матрица размерности 1×1:

A = 5;

ndims(A)

ans =

size(A)

ans =

1 1

Функция isscalar определяет, содержит ли переменная скалярную величину:

isscalar(A)

ans =

Векторы. Вектор – это матрица, одина из размерностей которой равна единице, а другие больше единицы. Пример числового вектора-строки:

A = [5.73 2-4i 9/7 25e3.046 sqrt(32) 8j]

size(A)

ans =

1 7

Пример числового вектора-столбца:

В = [5.36; 7.01; 9.44]

В =

5.36

7.01

9.44

size(В)

ans =

3 1

isvector(А), isvector(В)

ans =

ans =

Матричные операции.

Сложение и вычитание матриц

Для сложения и вычитания матриц необходимо, чтобы обе матрицы имели одинаковый размер или одна из них была скаляром. Сложение и вычитании матриц осуществляется поэлементно. Например,

A = pascal(3);

B = magic(3);

X = A + B

X =

9 2 7

4 7 10

5 12 8

Y = X – A

Y =

8 1 6

3 5 7

4 9 2

Векторное произведение и транспонирование

Вектор-строка и вектор-столбец могут быть перемножены, если они имеют одинаковую длину. Имеется два вида произведения векторов – внутреннее и внешнее. Результатом внутреннего произведения является вектор, а внешнего – матрица. Например:

v = [2 0 -1];

u = [3; 1; 4];

x = v*u

x =

y = u*v

y =

6 0 -3

2 0 -1

8 0 -4

Для матриц с вещественными элементами, операция транспонирования (оператор апостроф (')) меняет местами a_ij и a_ji. MATLAB использует также оператор апостроф (') для транспонирования матриц с комплексными числами, при этом кроме транспонирования комплексные числа заменяются на комплексно-сопряженные. Для транспонирования матриц с комплексными числами без замены на комплексно-сопряженные, используется оператор точка-апостроф (.'). Например,

B = magic(3)

X = B'

B =

8 1 6

3 5 7

4 9 2

X =

8 3 4

1 5 9

6 7 2

Транспонирование превращает вектор-строку в вектор-столбец, и наоборот:

x = v'

x =

-1

y = u'

y =

3 1 4

Умножение матриц. Произведение матриц определяется таким образом, чтобы отражать состав базовфых линейных преобразований и обеспечивать компактное представление систем совместимых линейных уравнений. Матричное произведение матриц C = AB определено, когда размерность столбцов матрицы A равна размерности строк матрицы B, или когда один из множителей скаляр. Если A имеет размерность m×p и B – размерность p×n, их произведение C имеет размерность m×n. Например,

A=[1 2 3;4 5 6];

B=[1 2;3 4; 5 6];

С=A*B

С =

22 28

49 64

Матрица может быть умножена справа на вектор-столбец (длина вектора-столбца должна быть равна длине строки матрицы) и слева на вектор-строку (длина вектора-строки должна быть равна длине столбца матрицы), например:

A=[1 2 3;4 5 6];

u = [3; 1; 4];

Х = A*u

Х =

B=[1 2;3 4; 5 6];

v = [2 0 -1];

Y = v*B

Y =

-3 -2

Любая матриц и любой вектор могут быть умножены на скаляр, например,

A=[1 2 3;4 5 6];

7*A

ans =

7 14 21

28 35 42

v = [2 0 -1];

3*v

ans =

6 0 -3

Единичная матрица (общепринятое обозначение I) – это матрица любой размерности, все элементы главной диагонали которой равны единице, а остальные элементы равны нулю. Эти матрицы имеют свойство, AI = A и IA = A в случае соответствия размерностей A и I. В MATLAB функция eye(m,n) возвращает единичную прямоугольную матрицу m×n и eye(n) возвращает единичную квадратную матрицу n×n.

Нормы векторов и матриц. p -норма вектора x

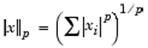
вычисляется функцией norm(x,p). Эта функция определена для любого значения p > 1, наиболее часто используемые значения p 1, 2, и ∞. По умолчанию p = 2, что соответствует Евклидовой длине:

v = [2 0 -1];

[norm(v,1) norm(v) norm(v,inf)]

ans =

3.0000 2.2361 2.0000

p -норма матрицы A,

может быть вычислена для p = 1, 2, and ∞ функцией norm(A,p). Опять, по умолчанию p = 2:

C = fix(10*rand(3,2));

[norm(C,1) norm(C) norm(C,inf)]

ans =

19.0000 14.8015 13.0000

Дата добавления: 2014-01-11