Т4. Если является комплексным корнем полинома , то комплексно-сопряженное число также является корнем этого полинома

Т3. (о разложении полинома на простые множители) Любой полином степени можно представить в виде произведения коэффициента при старшей степени на множителей вида, где – корни уравнения, т.е.

Т2. Любой полином степени имеет хотя бы один корень (действительный или мнимый).

Сл.Если является корнем уравнения, то остаток деления равен нулю, т.е..

Рассмотрим основные теоремы алгебры:

.

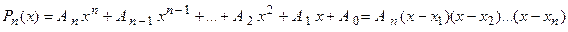Док-во. Воспользуемся следствием из теоремы Безу: . Поступая аналогично, найдем, что

, …, , .

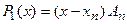Пример 1. Разложить на простые множители полином .

Найдем корни уравнения . Дискриминант уравнения 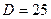, следовательно, 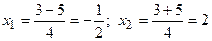. Таким образом, разложение полинома на простые множители имеет вид: .

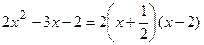Пример 2. Найти корни полинома .

Найдем корни уравнения 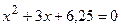. Дискриминант уравнения 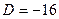, следовательно, . Отсюда видно, что .

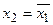З1. Из данного примера видно, что комплексно-сопряженные корни представляются в разложении полинома на простые множители в виде квадратных многочленов с отрицательными дискриминантами.

О1. Если корень 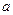повторяется в разложении полинома на простые мно-жители 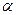раз, то он называется кратным корнем или корнем кратности .

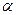Пример 3. Разложить на простые множители полином .

Данный полином представляет собой полный квадрат, поэтому после сворачивания он принимает вид , т.е. корень является корнем кратности 2.

2. Итегрирование рациональных дробей.

Метод неопределенных коэффициентов.

О2. Отношение двух полиномов 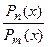называется рациональной дробью. Если , то дробь называется правильной, а в случае, когда 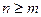– неправильной.

Пример 4. Выяснить, какие дроби явлются правильными, а какие – непра-вильными:

а) 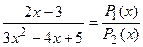– правильная рациональная дробь;

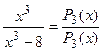
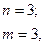
б) – неправильная рациональная дробь;

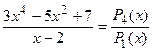
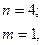
в) 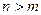– неправильная рациональная дробь.

Если рациональная дробь неправильная, то можно выделить “целую” часть так же, как и в случае обычной неправильной дроби:

_ 257 3 – знаменатель дроби

85 – целая часть

_ 17

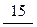
2 – остаток деления

При делении полинома на полином надо обращать внимание на старшие степени этих полиномов и числовые множители при них. В качестве примера выделения “целой” части у неправильной дроби рассмотрим отношение

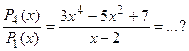
Итак, 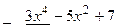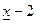– знаменатель дроби

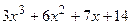– «целая часть»

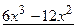
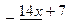
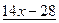
– остаток деления

Таким образом, можно записать, что .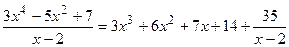

З2. Деление числителя на знаменатель дроби прекращается тогда, когда в остатке деления получается полином, порядок которого становится меньше порядка полинома, стоящего в знаменателе.

Итегрирование рациональных дробей проводится по следующей методической схеме: Если рациональная дробь неправильная, то выделяют “целую” часть, которая легко интегрируется (интегралы от “целой” части являются табличными (см. таблицу неопределенных интегралов от степенной функции в Лекции № 1 Второго семестра)) и правильную рациональную дробь, интегрирование которой проводится следующим образом (покажем схему на конкретном примере):

Пример 5. Вычислить .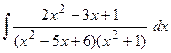

Дата добавления: 2014-01-11