Сходимость положительных рядов

Схема проектирования безопасности деятельности

Рассмотренные методологические вопросы безопасности позволяют представить проектирование безопасных условий деятельности в виде ло­гической последовательности (алгоритма) необходимых действий и соот­ветствующих им результатов.

Логико-методическая схема анализа и проектирования безопасности деятельности

Последовательность действий

Результат действий

1. Декомпозиция проектируемых или существующих объектов на элементы   2. Идентификация опасностей, создаваемых каждым элемен­том, определенным в п.1 3. Построение "дерева причин и опасностей" 4. Количественная и качествен­ная оценка опасностей, сра­внение с допускаемыми значе­ниями и уровнем риска 5. Определение целей     6. Комплексная оценка объектов по параметрам безопасности 7. Анализ возможных принципов, методов и средств обеспече­ния безопасности 8. Анализ достоинств и недос­татков, потерь и выгод по каждой альтернативе 9. Анализ приемлемых методов, принципов и средств 10. Расчёты 11. Оценка эффективности

Конкретизируются: 1. Предметы труда 2. Средства труда: машины, сооружения, здания 3. Продукты труда, полуфабрикат 4. Энергия (электрическая, пневматическая и др.) 5. Технологические процессы, операции, действия 6. Природно-климатические факторы 7. Растения, животные 8. Персонал 9. Рабочие места, цехи, участки и т.д. Перечень опасностей     Причины опасностей   Перечень причин и опасностей, защита от которых необходима     Количественное определение па­раметров условий труда, которые должны быть достигнуты Принятые интегральные или балльные показатели Набор принципов, методов, альтернатив     Выбор приемлемого варианта     Выбор конкретных методов, средств, принципов Конкретные решения Показатели технического, социального, экономического эффектов

Пусть имеем ряд A: 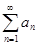, в котором все члены положительные: 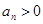(члены, равные нулю, можно выбросить из ряда без ущерба для сходимости-расходимости ряда).

Лемма. Если частичные суммы ряда S_n= a₁ + a₂+ … + a_n с положительными членами ограничены сверху (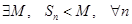), то ряд А сходится. Это связано с тем, что последовательность частичных сумм 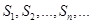строго монотонна и ограничена сверху. Следовательно, она имеет предел.

Признак сравнения. Пусть даны два ряда:

Пусть 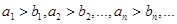Тогда из сходимости ряда А следует сходимость ряда В, из расходимости ряда В следует расходимость ряда А.

Действительно, если сходится ряд А, то есть если он имеет сумму, то частичные суммы ряда В будут ограничены сверху и будут строго монотонно возрастающими. По уже упоминавшемуся свойству монотонных ограниченных сверху последовательностей, частичные суммы ряда В будут иметь предел, ряд В также сходится.

Аналогично, если ряд В расходится, то это означает, что его частичные суммы неограничены сверху. Но тогда и последовательность частичных сумм ряда А будет неограниченной сверху и предела иметь не будет, ряд А также расходится.

На практике признак сравнения часто удобно применять в следующей предельной форме. Пусть есть ряды:

Если существует предел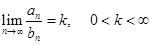, то ряды А и В сходятся одновременно (или расходятся одновременно).

Если же k= 0, то из сходимости ряда В следует сходимость ряда А. При k=¥, из расходимости ряда В следует расходимость ряда А.

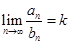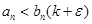Действительно, если , то для . Следовательно, для всех n>N. Тогда из сходимости ряда В: следует сходимость ряда и сходимость .

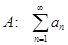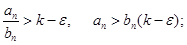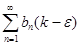Пусть ряд В расходится. Тогда Ряд расходится, следовательно и ряд 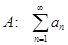расходится.

В частности, расходимость гармонического ряда 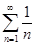следует из сравнения с расходящимся рядом 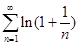, ибо .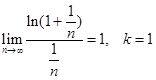

Еще пример: ряд 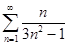расходится, ибо 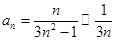, а ряд 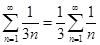расходится.

Дата добавления: 2014-01-11