Сходимость произвольных рядов

Ниже будут рассматриваться ряды, в которых имеется бесконечное количество положительных членов и бесконечное количество отрицательных членов. Такие ряды называют знакопеременными.

Остановимся сначала на рядах знакочередующихся. Их удобно записывать так: . Здесь полагаем все. В таком ряде знаки + и - чередуются и идут через один, откуда и название ряда.

Достаточный признак сходимости знакочередующегося ряда:

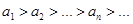Признак Лейбница. Если члены ряда : монотонно убывают: и если общий член стремится к нулю (), то ряд сходится. Cходящийся ряд называют рядом лейбницевского типа.

Для доказательства сначала рассмотрим частичные суммы с четными номерами:. Объединяем слагаемые в этой сумме: 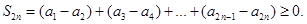Таким образом, равна сумме положительных слагаемых и следовательно, не убывает, является монотонно возрастающей последовательностью. Она ограничена сверху: . Итак, 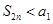- последовательность ограничена сверху. Она имеет предел: . Но если перейти к суммам нечетным, то будем иметь: . 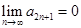Поскольку предел , то имеем окончательно: 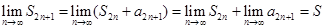. Другими словами, четные и нечетные частичные суммы имеют один и тот же предел. Отсюда заключаем, что ряд сходится. Попутно мы доказали, что .

На основании этого неравенства удобно оценивать сумму остатков и . Имеем: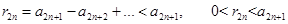

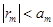Ясно, что . Объединяя неравенства для и , можно написать , где m – произвольное натуральное число, четное или нечетное. Таким образом, при замене суммы знакочередующегося ряда Лейбница на его частичную сумму мы совершаем ошибку, не превосходящую (по модулю) первого отброшенного члена рядя.

Пример 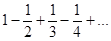- ряд сходится по признаку Лейбница, ибо 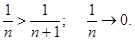Это ряд Лейбница. Позже будет показано, что .

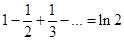Требование монотонности стремления членов знакочередующегося ряда к нулю существенное для его сходимости. Если оно не выполнено, то возможна расходимость ряда, несмотря на стремление к нулю его членов. В качестве примера такого поведения рассмотрим ряд: 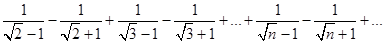. Члены этого ряда не удовлетворяют условию монотонности стремления к нулю: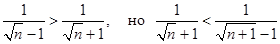. Для него имеем: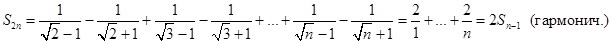

Но гармонический ряд расходится, поэтому рассмотренный знакочередующийся ряд также расходится.

Заметим, что в теореме Лейбница условия монотонности можно ослабить. Достаточно потребовать монотонности членов ряда, начиная с некоторого места (номера n). Т.е. первые члены знакочередующегося ряда могут не удовлетворять условию монотонности.

Поэтому если рассмотреть ряд 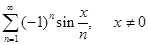, то увидим, что при любом фиксированном x, для достаточно больших n, имеет один определенный знак, и имеем ослабление условий, ряд сходится при любом x.

Дата добавления: 2014-01-11