
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Переместительное свойство абсолютно сходящихся рядов
|
|
|
|
Если ряд 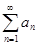 сходится абсолютно, то сходится (также абсолютно) и ряд
сходится абсолютно, то сходится (также абсолютно) и ряд 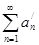 , полученный произвольной перестановкой членов исходного ряда.
, полученный произвольной перестановкой членов исходного ряда.
Существенно отметить, что перестановке могут подвергаться бесконечное множество членов исходного ряда.
Докажем. Пусть сначала имеем знакоположительный ряд 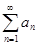 , т.е. для всех n, an> 0. Так как по нашему условию он сходится, то можно писать
, т.е. для всех n, an> 0. Так как по нашему условию он сходится, то можно писать 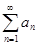 = S0, S0 – определенная величина. Рассмотрим k -ую частичную сумму ряда
= S0, S0 – определенная величина. Рассмотрим k -ую частичную сумму ряда 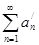 :
: 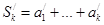 . Очевидно,
. Очевидно, 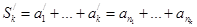 . Обозначим N= max (n1,…,nk). Тогда имеем очевидное неравенство:
. Обозначим N= max (n1,…,nk). Тогда имеем очевидное неравенство: 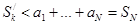 , ибо среди членов частичной суммы SN есть и члены
, ибо среди членов частичной суммы SN есть и члены 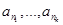 . Но SN £ S0 при любом N. Итак, при любом k имеем
. Но SN £ S0 при любом N. Итак, при любом k имеем 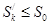 . Следовательно, частичные суммы
. Следовательно, частичные суммы 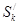 ряда
ряда 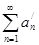 не только монотонно возрастают, но и ограничены сверху. Следовательно, последовательность
не только монотонно возрастают, но и ограничены сверху. Следовательно, последовательность 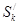 имеет предел при k®¥, то есть ряд
имеет предел при k®¥, то есть ряд 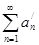 сходится. При этом для его суммы
сходится. При этом для его суммы  имеет место неравенство:
имеет место неравенство: 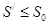 . Далее, меняя (в рассуждениях) ряды
. Далее, меняя (в рассуждениях) ряды 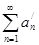 и
и 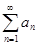 местами, можно доказать и неравенство:
местами, можно доказать и неравенство: 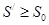 . Откуда получаем единственно возможное и непротиворечивое равенство:
. Откуда получаем единственно возможное и непротиворечивое равенство: 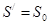 - суммы у рядов
- суммы у рядов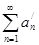 и
и 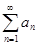 одинаковые.
одинаковые.
Если ряд 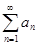 абсолютно сходится, то абсолютно сходится и ряд
абсолютно сходится, то абсолютно сходится и ряд 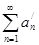 .
.
Для неабсолютно сходящихся рядов отметим два следующих свойства, которые следует иметь в виду при работе с такими рядами.
1. Можно показать, что если ряд 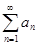 сходится неабсолютно, то ряд, составленный из одних только положительных его членов P:
сходится неабсолютно, то ряд, составленный из одних только положительных его членов P: 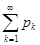 и ряд, составленный из одних только отрицательных его членов Q:
и ряд, составленный из одних только отрицательных его членов Q: 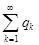 расходятся (не сходятся). Подчеркнем, что pk есть положительное
расходятся (не сходятся). Подчеркнем, что pk есть положительное 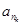 , а qk есть
, а qk есть 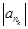 , причем здесь само
, причем здесь само 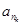 - отрицательное. Поясним кратко причину такого свойства условно сходящегося ряда.
- отрицательное. Поясним кратко причину такого свойства условно сходящегося ряда.
Ибо если сходится ряд P и сходится ряд A: 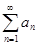 , то имеем:
, то имеем: 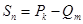 (
(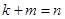 ), где
), где 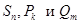 - частичные суммы рядов A, P и Q cоответственно. Нам известно, что существуют пределы последовательностей
- частичные суммы рядов A, P и Q cоответственно. Нам известно, что существуют пределы последовательностей 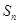 и
и 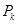 , следовательно существует и предел последовательности
, следовательно существует и предел последовательности 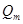 . Но тогда существует и предел суммы
. Но тогда существует и предел суммы 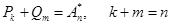 ,
,
т.е. сходится ряд  , чего нет на самом деле. Следовательно, ряды из только положительных членов и из только отрицательных членов условно сходящегося ряда расходятся, несмотря на то, что
, чего нет на самом деле. Следовательно, ряды из только положительных членов и из только отрицательных членов условно сходящегося ряда расходятся, несмотря на то, что 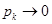 и
и 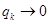 при
при 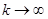 .
.
2. На этом основании можно доказать второе вышеупомянутое свойство условно сходящихся рядов (теорему Римана): в условно сходящемся ряде 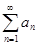 можно так переставить члены, что его сумма будет равна любому наперед заданному числу B.
можно так переставить члены, что его сумма будет равна любому наперед заданному числу B.
Например
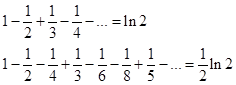
Наметим путь доказательства теоремы: Задаем число B. Из ряда 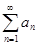 берем сначала только положительные члены
берем сначала только положительные члены 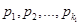 в таком количестве, чтобы выполнилось неравенство:
в таком количестве, чтобы выполнилось неравенство: 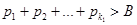 . Затем берем отрицательные члены ряда
. Затем берем отрицательные члены ряда 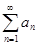 :
: 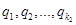 (все q <0) в таком количестве, чтобы было неравенство в другую сторону:
(все q <0) в таком количестве, чтобы было неравенство в другую сторону: 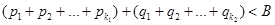 . Процесс прибавления новых положительных и новых отрицательных членов повторяем неограниченно. Уклонение получающихся сумм (фактически частичных сумм ряда с переставленными членами) от числа В не превосходит
. Процесс прибавления новых положительных и новых отрицательных членов повторяем неограниченно. Уклонение получающихся сумм (фактически частичных сумм ряда с переставленными членами) от числа В не превосходит 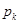 или
или 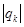 , k – достаточно большое. Следовательно, с ростом k уклонение новых частичных сумм от числа В стремится к нулю, так что сумма нового ряда, составленного из членов ряда
, k – достаточно большое. Следовательно, с ростом k уклонение новых частичных сумм от числа В стремится к нулю, так что сумма нового ряда, составленного из членов ряда 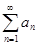 , будет равна В, что и требуется доказать в теореме Римана.
, будет равна В, что и требуется доказать в теореме Римана.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1724; Нарушение авторских прав?; Мы поможем в написании вашей работы!