Преимущества и недостатки различных схем хранения матриц

Для хранения разреженных матриц используется множество различних схем хранения, две из которых были продемонстрированы выше. При выборе конкретной схемы хранения надо обязательно принимать во внимание саму задачу, для решения которой используется та или иная схема хранения матрицы, и выбранный для нее метод решения.

Достоинство ленточного способа хранения разреженной матрицы - в его простоте. Однако у него есть и некоторые потенциально серьезные слабости. Прежде всего, если 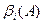сильно меняется при изменении 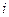, то диагональная схема хранения будет неэффективной (рис.5). Действительно, для примера, приведенного на рис.5, где ширина ленты равна 6, хранение матрицы по ленточной схеме не имеет никакого преимущества перед обычным хранением матрицы в виде двумерного массива.

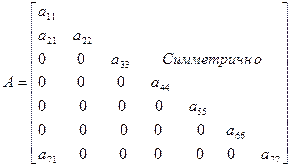
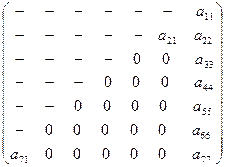
Рис.5.

Кроме того, имеются некоторые очень разреженные задачи, которые могут быть решены весьма эффективно, однако их нельзя упорядочить так, чтобы они имели малую ширину ленты. Таким образом, существуют задачи, для которых ленточные методы малопригодны.

Профильная схема хранения является более сложной в реализации, но при ее использовании учет разреженности матрицы проводится более эффективно, чем в ленточной схеме. Так для примера, приведенного на рис.5, оболочка матрицы будет определяться так, как показано на рис.6, а профиль равен 7, что явно говорит в пользу профильной схемы хранения матрицы в рассматриваемом примере.

Рис.6.

Дата добавления: 2014-01-11