Вывод преобразований Лоренца из требований

инвариантности уравнений Максвелла.

"Путь, которым шел Эйнштейн при открытии СТО, был крут и утомителен. Чтобы пройти его, потребовался глубокий анализ понятий пространства и времени и некоторые остроумнейшие мысленные эксперименты.

Путь, который мы собираемся избрать, будет широк и удобен. Мы будем исходить из всеобщей применимости уравнений Максвелла и огромного экспериментального материала, лежащего в их основе; наш путь (почти внезапно) окончится преобразованиями Лоренца со всеми их релятивистскими следствиями". А.Зоммерфельд.

Пункт 1. Четырехпотенциал и четырёхплотность тока.

Как известно, уравнения Максвелла могут быть представлены в виде двух волновых уравнений относительно векторного потенциала и скалярного потенциала 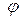. В вакууме они имеют вид

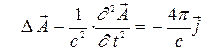; (1а)

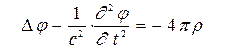. (1б)

Необходимо помнить, что представление уравнений Максвелла в виде (1) возможно лишь при учете дополнительного соотношения (калибровки Лоренца)

. (2)

Кроме того, полезно принять во внимание, что переменные части стороннего тока 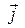и стороннего заряда 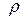связаны уравнением непрерывности

. (3)

Вначале обратим внимание на то, что, вводя новые координаты

, (4)

мы можем преобразовать оператор в левой части каждого волнового уравнения (1) к более компактному виду

. (5)

В операторе  (даламбертиане) легко узнать четырехмерное обобщение оператора Лапласа. С помощью  удаётся записать уравнения (1) в ещё более компактной форме

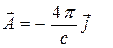 , . (6)

Эти координаты называются мировыми координатами. С их помощью все мировые события определяются в пространстве и во времени. Любому событию, имеющему координаты (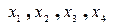), можно поставить в соответствие четырехобразование 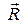, по форме напоминающее 4- вектор с проекциями (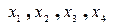). Это четырехобразование действительно имеет реальные признаки вектора в четырехмерном пространстве, который связывает координаты двух событий. Первое событие имеет координаты (0, 0, 0, 0) и заключается, например, в принятии решения о необходимости регистрировать все остальные события. Вторым является событие с координатами (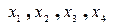). При таком подходе координаты любой пары событий в четырехмерном пространстве теперь тоже суть начала и концы векторов, которые характеризуют причинно-следственные связи между событиями. Однако определение 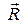как истинного вектора в четырёхмерном пространстве должно быть дополнено еще одним математическим условием

, (7*)

которому должны удовлетворять все истинные вектора и которое пока не доказано.

Подобно независимым координатам объединим потенциалы и 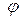в одно четырехмерное образование четырехпотенциал с компонентами

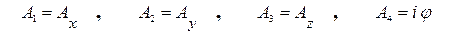(8)_A

и введём также четырехмерное образование четырёхплотность тока

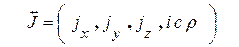. (8)_J

Оба волновых уравнения (6) объединяются в одно четырёхкомпонентное уравнение

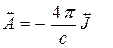 . (8)

Перейдем теперь к связывающему потенциалы и 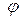дополнительному соотношению (2). Согласно (4) и (8)_A второй член в левой части калибровки Лоренца перепишется в виде

,

а все соотношение примет вид

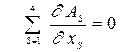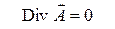(). (9)

Аналогичным образом можно преобразовать уравнение непрерывности

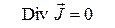(). (10)

В результате уравнения Максвелла примут наиболее компактную форму

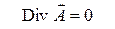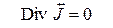, , . (11)

Основной задачей данного этапа является отыскание преобразований координат 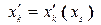и компонент 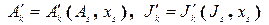двух новых четырёхобразований, в результате которых вид уравнений (11) оставался бы неизменным (или инвариантным).

Оказывается, что решить такую задачу нетрудно, если немного знать векторную алгебру трехмерного пространства. Из трёхмерной векторной алгебры известно, что уравнения типа (11) для какого-то трехмерного образования при переходе к другой системе координат останутся инвариантными, если компоненты преобразуются как компоненты вектора (т.е. компоненты удовлетворяют соотношению (7*) иявляется вектором), а преобразование координат является линейным и ортогональным преобразованием.

Свято веруя в корректность гипотезы о равноправии всех инерциальных систем отсчета, и, таким образом, в необходимость инвариантной записи уравнений Максвелла во всех ИСО в виде (11), А. Эйнштейн и вслед за ним мы делаем два фундаментальных утверждения, фактически формулируя два закона природы.

1. Четырехобразования и являются векторами в четырехмерном пространстве (или 4-векторами). В этом законе (понятии) заключено утверждение относительно поведения компонент 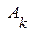и 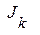при преобразовании мировых координат 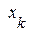. Суть закона в том, что при любом преобразовании координат компоненты 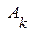и 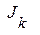должны преобразовываться как компоненты вектора в четырехмерном пространстве. Причем в качестве принципиально нового здесь имеется в виду связь четвертых компонент с тремя остальными.

Как четырехвектора и должны удовлетворять нескольким вполне определенным свойствам:

1) Скалярное произведение четырёхвектора на самого на себя («модуль» вектора или его «квадрат») не должно зависеть от системы координат:

( · ) = const_А, ( × )= const_J. (7*)

2) Скалярное произведение двух любых четырехвекторов не должно зависеть от системы координат. А поэтому справедливо, например, такое соотношение

( × )= const_AJ.

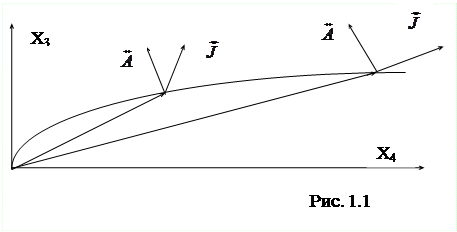
3) Вдоль какой-то мировой линии (траектории в четырехмерном пространстве) векторы и , разумеется, могут меняться (Рис. 1.1). Но в каждой точке четырехмерного пространства величина и "направление" (или "ориентация") каждого вектора не зависят от системы координат, которая выбрана для описания событий.

Пункт 2. Связь между мировыми координатами событий в разных ИСО

2. Мировые координаты одного и того же события в разных инерциальных системах отсчета связаны между собой только линейными ортогональными преобразованиями. В этом состоит второй закон природы. Его второй смысл заключается в том, что четырехобразование 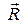есть истинный вектор в смысле формулы (7*).

Итак, в аспекте связи координат и времени в двух разных ИСО возможны лишь линейные ортогональные преобразования типа

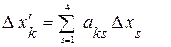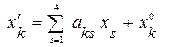(), (12)

в которых коэффициенты 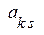являются постоянными величинами, связанными между собой соотношениями

, (13)

где 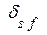– символы Кронекера.

Прежде всего, разберемся в физической природе трёх вариантов преобразований координат (12) на примерах трехмерного пространства.

а) 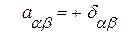, , 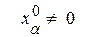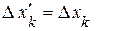. (14a)

Это преобразование обозначает перенос координат. Обобщая (14а) на четырехмерный случай, включим в него изменение начала отсчета времени и тем самым дополним его физический смысл. Преобразование связывает координаты двух неподвижных СО и потому не имеет отношения к обсуждаемой проблеме.

б) , , 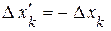. (14б)

Переход от штрихованных координат к нештрихованным осуществляется с помощью преобразования, где штрихованные и нештрихованные координаты нужно поменять местами, а заменить на ().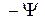

Теперь применим это ортогональное преобразование к нашему псевдодействительному четырехмерному пространству. Математически оно должно выражаться как вращение четырехмерной СК в пространстве 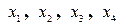. Всякое вращение в четырехпространстве можно разложить на 6 вращений в плоскостях (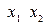), (), (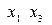), (), (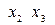), ()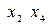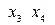. Вращения в первых трёх плоскостях соответствуют пространственным поворотам и потому преобразуют только пространственные координаты. Поэтому основной интерес в аспекте изменения времени в разных ИСО представляют вращения в плоскостях, содержащих ось OX₄.

Рассмотрим по аналогии с (16) "повороты" в плоскости (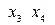) псевдодействительного пространства. Если угол 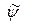есть '' угол поворота'' в псевдодействительном пространстве, то согласно (16) и (15) имеем

. 17)

Если событие 1) является началом отсчёта в обеих системах координат, то имеем

. (17')

В (17) компоненты четырёхобразования

(18)

по существу связаны между собой как проекции четырёхвектора (направленного из мировых координат события 1) в точку мировых координат 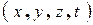события 2) на оси двух разных инерциальных систем отсчёта в четырёхмерном пространстве. Поскольку мы ищем преобразование разности координат двух событий в ИСО неподвижной и в движущейся относительно неё, то угол 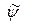должен зависеть только от величины скорости 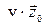системы 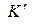относительно .

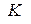В качестве примера, с помощью которого можно установить достаточно простую связь между координатами двух разных событий в двух различных ИСО и явную зависимость угла 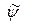от скорости 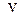, рассмотрим движение в системе 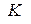начала координат системы 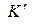. При этом будем считать, что в начальные моменты времени начала координат этой пары ИСО совпадали. Такими событиями могут быть, например, старт в 00 часов самолёта с аэродрома и одно из происшествий внутри самолёта через некоторый промежуток времени. Первое событие в обеих ИСО имеет все четыре координаты, равные нулю. Провожающие и пассажиры следят по своим синхронизированным на аэродроме часам за происходящим в самолете (вторым) событием. Его пространственные координаты в движущейся ИСО (самолёте) равны нулю. Поскольку в этом простом частном случае

; ;

;

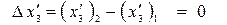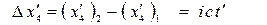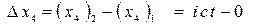
то из первой формулы (17) получаем

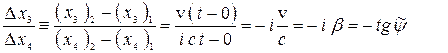(19)

явную зависимость от скорости 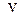угла 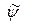''поворота'' СК в псевдодействительном пространстве. Выражая 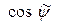и в виде соотношений

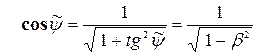,, (19)

получим из (17) формулы

; . (20)

Поскольку первое событие в каждой системе отсчёта находится в начале координат, то из формул (20) получаются выражения

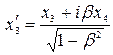; , (20´)

с помощью которых через координаты () второго события , установленные диспетчерами аэропорта, можно определить координаты () этого события, записанные пилотами в «черном ящике» самолёта.

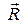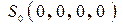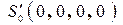На другом языке можно сказать, что формулы (20) являют собой однозначные соотношения между компонентами в двух разных ИСО четырёхобразования 1) , связывающего мировые координаты двух произвольных событий. В частном случае, когда одно событие (старт самолёта с аэродрома в полночь) в обеих ИСО имеет одинаковые нулевые координаты и , преобразования (20) компонент четырёхобразования 2) трансформируются в наиболее простую форму (20'), в которой координаты второго события в разных ИСО выражаются друг через друга как бы без привлечения координат первого события.

К соотношениям (20) необходимо добавить ещё два соотношения (равенства)

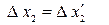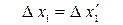; , (20)

которые связывают два компонента четырёхобразования 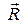, ориентированные ортогонально скорости 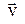. В рассматриваемом конкретном примере они равны нулю, но, разумеется, могут отличаться от нуля в общем случае.

Переходя к переменным 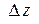и , из формул (20) получим

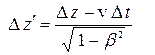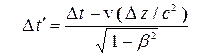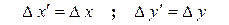; ; . (21)

Обратные преобразования согласно (16) получаются из (21) заменой 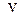на 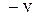, штрихованных координат на нештрихованные, и наоборот. Эти "обратные формулы" можно легко получить самостоятельно, если разрешить (21) относительно 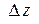и .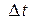

В предельном случае при (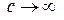) и и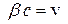з формул преобразования Лоренца получаются формулы преобразования Галилея

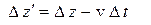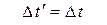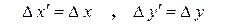, ,. (В. 1)

При 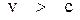в формулах (21) координаты становятся мнимыми. Это значит, что 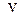не может быть больше .

Из (21) видно также, что 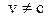, ибо при 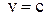знаменатель (21) обращается в нуль.

1) Пока что нельзя считать четырёхвектором, а его компоненты считать проекциями четырёхвектора.

2) Соотношения (20) позволяют установить связь между координатами двух событий в двух ИСО в произвольном случае.

Дата добавления: 2014-01-11