
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логічні основи комп'ютерної схемотехніки
|
|
|
|
Лекція №3. Основи булевої алгебри
ПЛАН:
1. Логічні основи комп'ютерної схемотехніки.
2. Аксіоми алгебри логіки
3. Мінімізація логічних елементів
4. Базові логічні елементи (комбінаційні схеми)
5. Реалізація логічних функцій із використанням комбінаційних схем
Література:
1. Прикладная теория цифровых автоматов / Самофалов К.Г., Романкевич А.М. и др. – Київ: Вища школа, 1987. – 369 с.
2. Бабич М. П., Жуков І. А. Комп’ютерна схемотехніка: Навчальний посібник. – К.: “МП-Прес”, 2004. – 412 с., іл.
Теоретичною основою комп'ютерної схемотехніки є алгебра логіки — наука, яка використовує математичні методи для розв'язання логічних задач. Алгебру логіки називають булевою на честь англійського математика Дж. Буля, який вніс найбільший вклад у розвиток цієї науки.
Основним предметом булевої алгебри є висловлювання — просте твердження, про яке можна стверджувати: істинне воно (позначають символом 1) або хибне (позначають символом 0). Зазвичай прості висловлювання позначають буквами, наприклад, Х\, Х2,..., Х,„ які у комп'ютерній схемотехніці називають змінними (аргументами). За допомогою логічних зв'язок НЕ, ЧИ, І, ЯКЩО... ТО... будують складні висловлювання, які називають мулевими (логічними) функціями і позначають буквами F, L, К, М, Р та ін.
Використання апарата алгебри логіки в комп'ютерній схемотехніці засноване на тому, що цифрові елементи характеризуються двома станами і через це можуть бути описані булевими функціями. Стандарт ДСТУ 2533-94 "Арифметичні і логічні операції. Терміни і визначення" конкретизував основні поняття булевої алгебри в системах оброблення інформації.
Змінну із скінченним числом значень (станів) називають перемикальною, а з двома значеннями — булевою. Функція, яка має як і кожна її змінна скінченне число значень, називається перемикальною (логічною). Логічна функція, число можливих значень якої і кожної її незалежної змінної дорівнює двом, є булевою. Таким чином, булева функція:— це окремий випадок перемикальної.
Операція — це чітко визначена дія над одним або декількома операндами, яка створює новий об'єкт (результат). У булевій операції операнди і результат набувають "булевого значення 1" (далі просто значення 1) і "булевого значення 0" (далі просто значення 0). Булеву операцію над одним операндом називають одномісною, над двома — двомісною і т.д.
Булеві функції можуть залежати від однієї, двох і в цілому від п змінних. Запис  означає, що деяка булева функція F залежить від змінних Х1,Х2, …, Хn. Основними булевими операціями є заперечення (операція НЕ, інверсія), диз'юнкція (операція ЧИ, логічне додавання, об'єднання) і кон'юнкція (операція І, логічне множення).
означає, що деяка булева функція F залежить від змінних Х1,Х2, …, Хn. Основними булевими операціями є заперечення (операція НЕ, інверсія), диз'юнкція (операція ЧИ, логічне додавання, об'єднання) і кон'юнкція (операція І, логічне множення).
Заперечення — це одномісна булева операція  (читається «не X» ), результатом якої є значення, протилежне значенню операнда.
(читається «не X» ), результатом якої є значення, протилежне значенню операнда.
Диз'юнкція — це булева операція 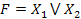 (читається «X1 чи Х2»), результатом якої є значення нуль тоді і тільки тоді, коли обидва операнди мають значення нуль.
(читається «X1 чи Х2»), результатом якої є значення нуль тоді і тільки тоді, коли обидва операнди мають значення нуль.
Кон'юнкція — це булева операція  (читається "Х1 і Х2"), результатом якої є значення одиниця тоді і тільки тоді, коли значення кожного операнда дорівнює одиниці. У виразі
(читається "Х1 і Х2"), результатом якої є значення одиниця тоді і тільки тоді, коли значення кожного операнда дорівнює одиниці. У виразі 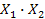 крапку можна опускати; часто застосовують записи
крапку можна опускати; часто застосовують записи  або
або  .
.
Операції заперечення, диз'юнкції і кон'юнкції можна задати за допомогою таблиць істинності, у яких зліва подані значення операндів, а справа — значення булевої функції.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2887; Нарушение авторских прав?; Мы поможем в написании вашей работы!