Релятивистская механика свободной материальной частицы

Реалізація логічних функцій із використанням комбінаційних схем

За допомогою суперпозицій, тобто підстановки в логічні формули замість змін­них деяких інших булевих виразів, можна одержати складніші функції будь-якого чи­сла змінних, наприклад

1)

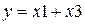
2)

3)

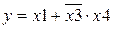
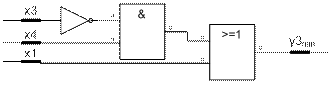
4)

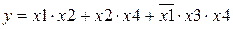
Наиболее общая формулировка закона движения механических систем даётся так называемым "принципом наименьшего действия" (или принципом Гамильтона). Согласно этому принципу каждая механическая система характеризуется определенной функцией обобщенных координат и импульсов , причем движение системы удовлетворяет следующему условию.

Пусть в моменты времени и система занимает определенные положения, характеризуемые двумя наборами значений координат и . Тогда между этими положениями система движется таким образом, чтобы интеграл

имел наименьшее возможное значение. Функция называется функцией Лагранжа данной системы, а интеграл - действием.

Рассмотрим две функции и , отличающиеся друг от друга на полную производную по времени от какой-либо функции координат и времени :

.

Вычисленные с помощью этих двух функций интегралы связаны соотношением

,

правая и левая части которого отличаются дополнительным членом, исчезающим при варьировании действия. Т.о., условие совпадает с условием , и вид уравнений остается неизменным. Это значит, что функция Лагранжа определена лишь с точностью до прибавления к ней полной производной по времени от любой функции координат и времени.

Другое доказательство того же утверждения можно представить в виде следующих математических соотношений:

,

ибо .

Пункт 1. Интеграл действия и функция Лагранжа свободной материальной частицы в ИСО.

Определим функцию Лагранжа свободной материальной частицы в ИСО, где – кинетическая и – потенциальная энергии. Поскольку пространство однородное, то не зависит от (можно считать, отсутствует). Поскольку время однородное, то и не зависят от времени. Следовательно, зависит только от . Поэтому тоже зависит только от .

В силу изотропии пространства функция не может зависеть также и от направления вектора , так что является функцией лишь его абсолютной величины (т.е. от квадрата )

. (1)

Обозначающий действие интеграл вдоль траектории частицы в мировом пространстве между двумя событиями

(2)

не должен зависеть от выбора той или иной ИСО. В противном случае в какой-то ИСО он был бы наименьшим, и эта ИСО была бы особой. Т.о., действие должно быть инвариантом относительно преобразования Лоренца (скаляром).

Далее из (2) ясно, что под интегралом должен стоять дифференциал от скаляра в первой степени. Однако единственный такой скаляр, который можно построить для свободной материальной частицы, движущейся по своей собственной траектории, есть собственное время объекта или пропорциональная ему величина (), где - постоянная, характеризующая данную частицу.

Как отмечалось в § 2, интеграл

имеет максимум при , т. е. при "перемещении" частицы вдоль прямой мировой линии, параллельной оси (когда частица в СО К находится в состоянии в одной точке). Аналогичным образом, если события в СО К не находятся в одной точке пространства, то можно выбрать СО К¢, в которой они одноместны. Тогда вновь интеграл между этими двумя событиями по прямой линии будет максимальным.

Создаваемая релятивистская теория движения материальных тел может получиться корректной только в том случае, если при движении тела по прямолинейной траектории действие будет минимальным, ибо именно в соответствии с этим принципом любая свободная материальная частица движется по прямой. Поэтому действие для рассмотренной свободной частицы должно иметь вид

, (3´)

где обозначает интеграл вдоль мировой линии между двумя выбранными событиями (т. е. между заданными мировыми координатами на траектории движения в 4-пространстве) и величина есть некоторая положительная постоянная, характеризующая данную частицу (). Сравнивая (2) и (3´), находим для свободной частицы в виде

. (3)

Величина , характеризующая частицу, по размерности должна быть энергией. В классической механике всякая частица характеризуется ее массой . Связь величин и находится из условия, что при предельном переходе наше выражение для должно перейти в классическое выражение . Для этого разложим в ряд по и, опуская члены высших порядков, получим

.

Поскольку в функции Лагранжа несущественны члены, являющиеся полными производными по времени, и постоянная величина () является именно таким членом, то при сравнении с классическим выражением её можно не учитывать. Опуская () и сопоставляя с , находим для постоянного коэффициента в формуле (3) явное выражение

. (4)

По размерности величина является энергией, что полностью отвечает физическому содержанию . Т.о., функция Лагранжа свободной материальной частицы может быть представлена в виде

. (5)

Пункт 2. Импульс и энергия свободной частицы

Импульсом частицы, как известно, называется вектор , компоненты которого равны производным от по компонентам () скорости . Символически вектор можно определить как градиент функции по компонентам скорости и, используя выражение (5), найти

. (6)

При малых скоростях (или в пределе при ) выражение (6) переходит в классическое.

По определению энергии системы найдём энергию свободной частицы

. (7)

Эта очень важная формула показывает, что в релятивистской механике энергия свободной частицы не обращается в нуль при , а остается конечной величиной

. (7')

Ее называют энергией покоя частицы. Именно из-за наличия энергия и функция Лагранжа не совпадают друг с другом в отсутствие потенциальной энергии (т.е. в однородном пространстве ).

При малых скоростях (или в пределе при ), разлагая (7) по степеням , получим такое выражение

, (7'')

которое за вычетом энергии покоя точно совпадает с классическим выражением для кинетической энергии частицы.

Сопоставляя формулы (6) и (7), можно заметить, что они перепишутся универсально

, (6*)¢

, (7*)

если под понимать величину

, (8)

которая зависит от скорости частицы в данной СО. Такая форма записи позволяет говорить об эквивалентности массы и энергии, понимая под этим возможность в разных единицах мерить одно и то же.

Т.о., энергия, измеряемая количеством "работы, которую тело может совершить", и масса, определяемая импульсом при данной скорости, являются взаимосвязанными понятиями: если есть одно, то есть и другое 1).

И еще один вывод : ни масса, ни энергия не инвариантны при преобразовании координат. Каждая величина согласно (7) и (8) зависит от СО наблюдателя. Масса покоя - минимальная масса, ибо находится в особой, выделенной СК, где тело покоится. Она скаляр и инвариант в том же смысле, в каком являются инвариантами СВО или длина стержня .

Из соотношений (6), (7), (8) можно получить полезные формулы, которые устанавливают связь между энергией, массой покоя и импульсом частицы. Исключая из выражений

величину , получим энергию в виде так называемой функции Гамильтона

.(9)

Соотношения (6), (7) и (8) позволяют также представить связь между и в виде

(10)

или, опуская вектора, в виде

. (10¢)

Частный случай. При (или ) энергия и импульс частицы обращаются в бесконечность. Это значит, что тело с отличной от нуля массой покоя не может двигаться со скоростью света. В релятивистской механике, однако, могут существовать частицы с массой покоя , которые движутся со скоростью света. Используя (10') для таких частиц имеем

. (10*)¢

Пункт 3. Уравнение движения релятивистской частицы.

Рассмотрим элементарную частицу в поле силы . Из теоретической механики известно, что под действием силы будет изменяться импульс частицы в соответствии с уравнением движения

, (**)

называемым в классической механике вторым законом Ньютона. Дифференцируя (6) по времени, получим релятивистский вариант уравнения движения элементарной частицы

. (11)

Представляют интерес два частных случая.

а) Сила . Поскольку скорость частицы изменяется только по направлению (но не по величине), то отсутствует составляющая ускорения, параллельная скорости. В этом случае , и уравнение движения имеет вид

. (11a)

Отношение силы к ускорению есть то, что было определено как масса (иногда ее называют поперечная масса ).

б) Сила . В этом случае скорость частицы изменяется только по величине и поэтому

.

Уравнение движения в этом случае имеет вид

, (11б)

и отношение силы к ускорению (продольная масса) имеет иную величину

1) В курсе общей физики масса определена как отношение силы к ускорению.

Дата добавления: 2014-01-11