Материальной точки. 4-сила Минковского

В силу равноправия всех ИСО уравнения (законы) механики должны быть инвариантны по отношению к преобразованию Лоренца. Это значит, что второй закон Ньютона должен быть представлен в виде равенства двух 4-екторов, один из которых есть 4-ектор силы, а другой 4-вектор по размерности и по смыслу есть производная от 4-импульса по времени. Очевидно, что время должно быть инвариантной величиной, т.е. собственным временем объекта. Тогда инвариантная запись уравнения движения имеет вид

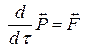. (10)

Она удовлетворяет требованию перехода к классической механике при 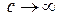. Поскольку известны компоненты 4-импульса (7) и связь 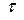и времени 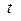, то левая часть уравнения (10) может быть представлена в виде

. (11)

Уравнения движения релятивистской частицы (3.11) позволяют установить связь между компонентами силы и компонентами производной от импульса в трёхмерном пространстве

. (12)

Сравнивая (10) – (12) друг с другом, найдем

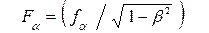(13)

связь трех компонент 4-силы и компонент вектора силы .

Умножим левую и правую части (10) на 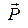. Тогда получим соотношение

,

из которого найдем

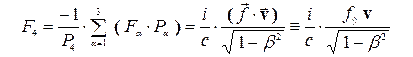. (14)

Т. о., из инвариантно записанного уравнения (10) получим выражение для 4-силы Минковского

. (15)

Преобразование силы происходит так же, как преобразование любого 4-вектора. Перейдем в СО, которая движется относительно первоначальной СО со скоростью , и в соответствии с общими правилами преобразуем 4-вектор силы

;

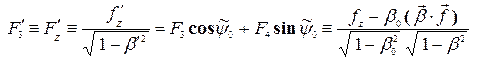; (16)

.

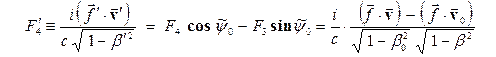Предположим, что осуществляется преобразование в СО К¢, где частица покоится (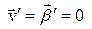). Поскольку скорость СО К' относительно СО К по условиям преобразования равна 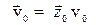, то и скорость частицы в К равна (т.е. ). Подставляя и 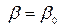в (16), найдём

. (16')

Отметим, что

1) Аналогичным образом в классической механике обычно три пространственные координаты задавались как функции четвертой независимой переменной времени, причем время было инвариантом преобразования Галилея.

2) Разделение 4-векторов на пространственно-подобные и времени-подобные имеет смысл во всех случаях.

Дата добавления: 2014-01-11