Геометрична інтерпретація системи диференційних рівнянь

Розглянемо динамічні системи, які моделюються кінцевим числом звичайних диференційних рівнянь. У розглянутому випадку для визначення динамічної системи необхідно вказати об'єкт, що допускає опис стану завданням величин x₁, x₂, …, x_N у деякий момент часу t=t_a Величини x_t можуть приймати довільні значення, причому двом різним наборам величин x_t і 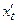відповідають два різних стани. Закон еволюції динамічної системи за часом записується системою звичайних диференційних рівнянь:

(*)

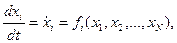
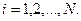Якщо розглядати величини x₁, x₂, …, x_N як координати точки x в N-мірному просторі, то виходить наочне геометричне подання стану динамічної системи у вигляді цієї точки, яку називають фазовою точкою, а простір станів – фазовим простором динамічної системи.

Зміні стану системи в часі відповідає рух фазової точки уздовж деякої лінії, яку називають фазовою траєкторією.

У фазовому просторі рівняннями системи (*) визначається векторне поле швидкостей, яке співставляє кожній точці x вектор швидкості F(x), який з неї виходить. Компоненти вектора x даються правими частинами рівнянь: 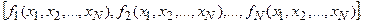Динамічна система (*) може бути записана у векторній формі:

(**)

де F(x) – вектор-функція розмірності N.

Необхідно уточнити взаємозв'язок понять числа ступенів свободи й розмірності фазового простору динамічної системи. Під числом ступенів свободи розуміється найменше число незалежних координат, необхідних для однозначного визначення стану системи.

Під координатами спочатку розумілися саме просторові змінні, що характеризують взаємне розташування тіл й об'єктів. У той же час для однозначного розв’язку відповідних рівнянь руху необхідно крім координат задати відповідні початкові значення імпульсів або швидкостей. У зв'язку із цим система з n ступенями свободи характеризується фазовим простором у два рази більшої розмірності (N = 2n).

Дата добавления: 2014-01-11