Матриця стійкості

Глобальний фазовий портрет особливо легко може бути побудований для консервативних одномірних систем. Важливу роль при цьому грають точки рівноваги, що характеризуються певним локальним поводженням: навколо стійких точок формуються сукупності замкнутих кривих: криві в околиці нестійких точок мають гіперболічний характер. У випадку неконсервативних систем, якщо явний розв’язок рівнянь руху невідомий, глобальний фазовий портрет побудувати складно. Однак завжди можна побудувати наближений локальний фазовий портрет, знайшовши точки рівноваги (які надалі ми будемо називати нерухомими точками) і намалювавши в їхній околиці фазові траєкторії.

Нерухомі точки можна розглядати як організуючі центри динаміки системи у фазовому просторі. Таким чином, визначивши ці точки й досліджений характер їхньої стійкості, можна побудувати глобальну картину поводження системи.

Розглянемо системи другого порядку загального виду:

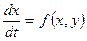, , (1)

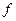де і 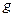являють собою довільні (звичайно нелінійні) гладкі функції аргументів 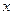та 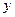. Нерухомими точками є такі значення 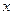та 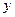, які позначені 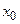та , для яких фазовий потік є стаціонарним (тобто ):

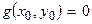, , (2)

Цим умовам може відповідати будь-яка кількість точок 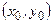залежно від точного вигляду функцій 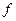та 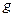. Після того, як ці точки знайдені, їхню стійкість можна визначити, вивчивши поведінку фазових траєкторій при малих зсувах в околиці . Розкладемо 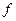та 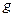в ряди Тейлора за степенями та :

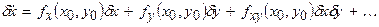, (3а)

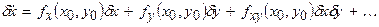. (3б)

Якщо обмежитися членами першого порядку, то (3) можна представити у вигляді лінійної системи (4), яку ми будемо називати “лінеаризованими” рівняннями:

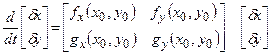(4)

де матрицю 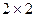(позначувану через М) часто називають матрицею стійкості. Система лінійних рівнянь першого порядку (4) (яку не складно узагальнити на випадок системи n-го порядку виду

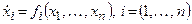
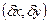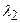легко розв'язується в термінах власних значень М, які власно і визначають стійкість відповідних нерухомих точок. Позначимо вектор-стовпець через , а два власних вектори, що відповідають двом власним значенням і через та ; тоді загальний розв’язок (4) являє собою лінійну комбінацію

, (5)

де с₁ та с₂ - довільні коефіцієнти, а власні значення є розв’язками рівняння

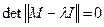, (6)

де – одинична матриця. Можна перевірити, що у випадку чисто уявних і 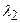, локально фазові траєкторії будуть являти собою замкнуті еліпси, що безсумнівно вказує на стійку нерухому точку. Якщо, навпроти, 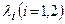мають дійсну частину, то траєкторії залежно від знака будуть загасати або зростати експоненціально, указуючи відповідно на певний тип стійкості або нестійкості. Існує цілий ряд комбінацій, кожній з яких відповідає нерухома точка певного типу; їхня класифікація приводиться нижче. Відзначимо, до речі, що хоча тип стійкості визначається власними значеннями та 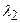, не слід також зневажати власними векторами 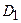та – їхній вид вказує напрямок локальних фазових потоків.

Дата добавления: 2014-01-11