Электромагнитном поле

Действие для частицы, движущейся в заданном электромагнитном поле, складывается из действия (3.3) свободной частицы и из члена, описывающего взаимодействие частицы с полем: 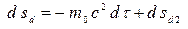. Последний должен содержать величины, характеризующие частицу и поле. Вид действия для частицы в электромагнитном поле определяется не только на основании общих соображений типа требования релятивистской инвариантности1), но и в результате опытных данных.

Свойства частицы в отношении ее взаимодействия с электромагнитным полем определяются только (одним параметром) зарядом частицы 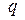, который может быть положительной или отрицательной (а также равной нулю) величиной. Свойства же поля характеризуются 4- потенциалом, компоненты которого являются функциями координат и времени. Эти величины должны входить в действие в виде члена

,

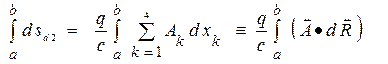где функции 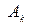берутся в точках мировой линии частицы. Множитель 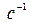существует из соображений размерности. Таким образом, действие для заряда в электромагнитном поле имеет вид

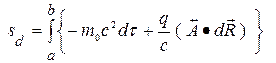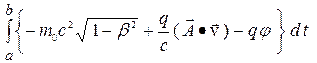º. (1)

При переходе от первой части формулы (1) ко второй были использованы выражения (1.7) для 4-потенциала 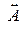и (1.4) для 4-вектора 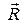, а также скорость частицы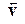. Подынтегральное выражение есть не что иное, как функция Лагранжа для заряда в электромагнитном поле

. (2)

Это выражение отличается от функции Лагранжа (3.5) для свободной частицы двумя последними членами, которые описывают взаимодействие заряда с полем.

Обобщенный импульс частицы находим по определению в виде

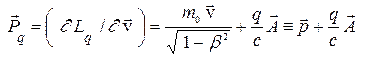(3)

и замечаем, что его часть 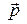является обычным импульсом материальной частицы, который мы будем называть просто импульсом. Из функции Лагранжа по известной формуле (3.7) получаем также энергию заряженной частицы в э.-м. поле в виде

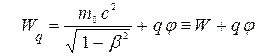. (4)

Функция Гамильтона в общепринятом представлении должна быть выражена не через скорость, а через обобщенный импульс частицы. Используя (3) и (4), по аналогии с (3.6) – (3.9) находим функцию Гамильтона в виде

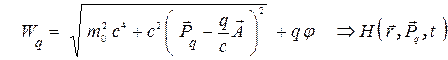. (5)

Для малых скоростей (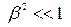) функция Лагранжа (2) переходит в

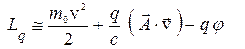. (2¢)

В этом приближении импульс частицы имеет вид

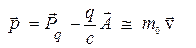, (3¢)

а выражение для функции Гамильтона -

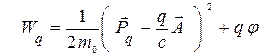. (5¢)

Пункт 3. Уравнения движения заряда в заданном поле.

Заряд не только подвергается воздействию со стороны поля, но, в свою очередь, сам влияет на поле, изменяя его. Однако его действием на поле можно пренебречь, если заряд 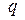мал. В этом приближении, рассматривая движение в заданном поле, можно считать, что само поле не зависит ни от координат, ни от скорости заряда. Точные условия, которым должен удовлетворять такой заряд, можно установить. Ниже мы будем считать эти условия выполненными.

1) Уравнения движения заряда в заданном электромагнитном поле, как и всякие уравнения Лагранжа, получаются варьированием действия и имеют вид

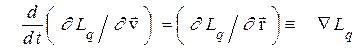, (6)

где 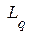определяется формулой (2) и где 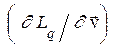есть обобщенный импульс частицы (3). Правая часть (6) определяется из (2) как

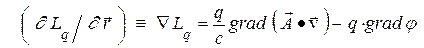
и преобразуется по известной формуле векторного анализа

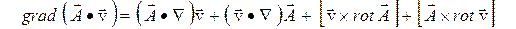
для двух произвольных векторов 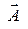и 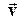к виду

.

Подставляя это выражение в (6), получим уравнения Лагранжа в виде

.

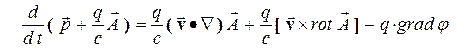Подставляя в последнее уравнение полную производную по 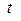от векторного потенциала

,

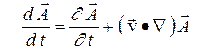получим уравнение движения частицы в электромагнитном поле

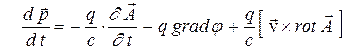. (7)

В левой части (7) стоит производная от импульса частицы по времени. Следовательно, выражение в правой части (7) есть сила, действующая на заряд в электромагнитном поле. Используя представления электрического и магнитного полей (5.2), преобразуем уравнение (7) к виду

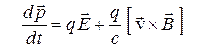. (8)

Стоящее справа выражение нам хорошо знакомо. Первая часть силы (8) не зависит от скорости заряда и ориентирована по направлению электрического поля 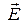. Вторая часть силы (8) пропорциональна скорости заряда и направлена перпендикулярно скорости и магнитному полю 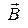. Это – сила Лоренца, которую мы получили в §5 из закона Кулона. Два разных пути привели к одному и тому же результату. Но в одном случае приходилось постулировать действие (или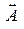), в другом – силу Кулона.

Для скоростей, малых по сравнению со скоростью света, импульс приближенно равен своему классическому выражению. Уравнение движения (8) переходит в этом случае в уравнение

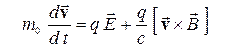. (8¢)

2) Выведем еще уравнение, определяющее изменение кинетической энергии частицы со временем. Поскольку кинетическая энергия 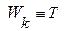и энергия покоя 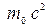совместно образуют энергию свободной движущейся частицы, то

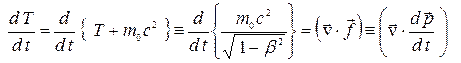. (9′)

При выводе уравнения (9′) использованы также соотношения

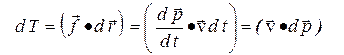или .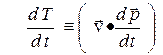

Подставляя в правую часть уравнения (9′) выражение 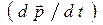из (8) и замечая, что 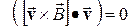, получим окончательный вариант уравнения изменения кинетической (механической) энергии заряженной частицы во внешнем поле

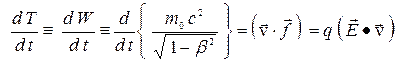. (9)

Изменение кинетической энергии со временем есть работа, произведенная полем над частицей в единицу времени. Из (9) видно, что эта работа равна произведению скорости заряда на силу, с которой действует на него электрическое поле. Работа поля при перемещении заряда на расстояние 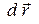за время 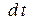равна, очевидно, (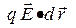). Подчеркнем, что работу над зарядом производит только электрическое поле. Магнитное поле не производит работы над движущимся зарядом и не изменяет его кинетическую энергию, поскольку сила, с которой магнитное поле действует на частицу, всегда перпендикулярна к ее скорости2).

Пункт 4. Движение заряда в постоянном однородном электрическом поле.

Рассмотрим движение заряда 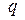в однородном постоянном электрическом поле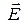 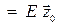, направленном вдоль оси ОZ. Из (8) следует, что движение будет происходить в одной плоскости, в качестве которой выберем плоскость ХОZ. Тогда уравнения движения (8) примут вид

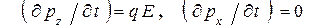. (10′)

Проинтегрируем эти уравнения, используя в качестве начальных условий (при 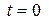) значения

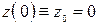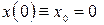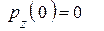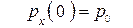; ; ; . (10′′)

В результате интегрирования получим

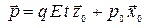. (10)

Кинетическая энергия частицы вместе с энергией покоя согласно (3.9) равна 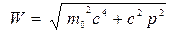. Подставляя в эту часть функции Гамильтона импульс движущейся частицы (10), находим в нашем случае

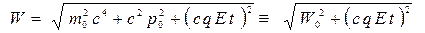, (11)

где 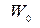– энергия частицы в начальный момент времени .

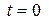Согласно (3.6¢) и (3.7¢) скорость частицы выражается формулой

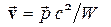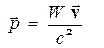; . (12)

Для изменения координаты частицы по направлению поля имеем уравнение

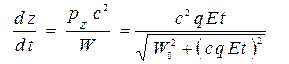, (12)_z

а для изменения координаты по направлению оси 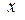получим уравнение в виде

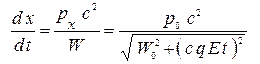. (12)_x

Интегрируя уравнение (12)_z с учётом начального условия (10''), находим выражение для координаты частицы по направлению оси 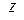в виде функции времени

. (13)_z

В результате интегрирования уравнения (12)_x найдем проекцию положения частицы на ось x -ов в виде функции времени

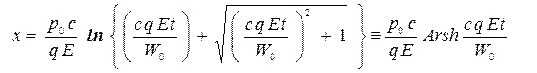.(13)_x

Выражая из (13)_x время 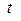как явную функцию

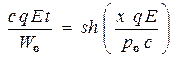(13')_x

координаты 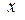и подставляя (13')_x в (13)_z, получим уравнение

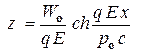(14)

траектории заряженной частицы в плоскости XOZ, которая называется цепной линией. Таким образом, с учётом релятивистских поправок заряженная элементарная частица движется в однородном электрическом поле по цепной линии.

Если скорость частицы 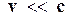, то (14) можно разложить в ряд по степеням 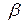и получить с точностью до членов высшего порядка малости уравнение траектории в виде параболы

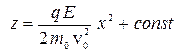. (14')

Именно такое уравнение траектории движения заряженной частицы в однородном поле было бы получено с помощью уравнений классической механики.

Пункт 5. Движение заряда в стационарном однородном магнитном поле

Рассмотрим движение заряда 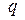в однородном магнитном поле 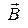. Выберем ось 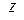по направлению магнитного поля. Используя согласно (3.10) в качестве импульса выражение (12) и принимая во внимание, что энергия частицы 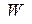в соответствии с (9) в магнитном поле постоянна, представим векторное уравнение движения в виде

1) Требования релятивистской инвариантности допускают наличие в (1) члена вида, где - скалярная функция. К тому же речь идет о классической (не квантовой) теории, и нигде не учитываются эффекты, связанные со спином частицы.

2) Уравнения механики инвариантны по отношению к перемене знака у времени. Это значит, что если согласно уравнениям механики возможно какое-либо движение системы частиц, то возможно и обратное движение, при котором система проходит те же состояния в обратном порядке. Другими словами, в механике оба направления течения времени равноправны (эквивалентны), и уравнения механики инвариантны по отношению к замене будущего прошедшим (время изотропно). Аналогичная инвариантность согласно (8) имеет место и при движении заряженных частиц в электромагнитном поле. При этом, однако, вместе с заменой на надо изменить знак магнитного поля. Действительно, легко видеть, что уравнения движения (8) не меняются, если произвести замену. При этом согласно (5.2) скалярный потенциал не меняется, а векторный меняет знак:. Таким образом, если в электромагнитном поле осуществляется какое-то движение, то возможно и обратное движение в поле с обратным направлением.

Дата добавления: 2014-01-11