Лексикографический порядок

Перестановки различных элементов

Смешанные системы счисления

Целое положительное число N однозначно представляется в системе счисления с основанием r

N = d₀ + d₁*r +d₂*r²+…+d_k*r^k

Из истории известно, что в древнем Вавилоне применяли основание 60, у майя – 20, в арабской системе счисления основание 10, в вычислительной технике широко используются основания 2ⁿ: 2, 8, 16.

В системе с основанием r имеются цифры от 0 до r-1, при фиксированном k можно представить числа в диапазоне от 0 до r^k+1-1.

Смешанная система счисления использует набор оснований r₀, r₁, r₂…Целое положительное число представляется в виде

N = d₀ + d₁* r₀ +d₂* r₀* r₁+…+d_k* r₀* r₁*…* r_k-1

Здесь 0 ≤ d_i < r_i. При фиксированном k числа представляются в диапазоне от 0 до r₀* r₁*…* r_k -1.

Примером использования смешанной системы счисления является представление времени в секундах, минутах, часах, сутках, неделях. В этой системе r₀ = r₁ = 60, r₂ = 24, r₃ = 7. Например, число 54283 в этой системе обозначает 5 недель, 4 суток, 2 часа, 8 минут и 3 секунды, что составляет

3 + 8*60 + 2*60*60 + 4*24*60*60 + 5*7*24*60*60 секунд.

Находит применения смешанная система счисления с факториалами, где

N = d₀ + d₁*1! +d₂*2!+…+d_k*k!

Здесь r₀ = 1, r₁ = 2,…, r_i = i +1; d₀ = 0; 0 ≤ d_i < i+1, а числа находятся в диапазоне от 0 до (k+1)! - 1. Например, число 29 представляется в этой системе как 10210. Действительно, 0 + 1*1! + 2*2! +0*3! + 1*4! = 29, а

29 | _1__

29 29 | _2__

0 28 14 | _3__

1 12 4 | _4__

2 4 1

Встречается система счисления с убывающими факториалами, в которой

N = d₀ + d₁*n +d₂*n*(n-1) +…+d_k*n(n-1)*…*(n-k+1)

В ней r₀ = n, r₁ = n-1,…, r_i = n-i; 0 ≤ d_i < n-i; k<n.

Перестановками множества {a₁, a₂, …, a_n} называются расположения этого множества в различном порядке. Перестановка определяется последовательностью индексов располагаемых элементов, поэтому можно считать, что переставляются числа {1, 2, …, n}. Число n считается порядком перестановки. Всего имеется n! Различных перестановок порядка n.

Есть разные способы представления перестановок. Простейший из них – указание последовательности чисел перестановки, например (2, 4, 1, 5, 3). Иногда удобно записывать перестановку в 2 строки, где первая задает места элементов, а вторая сами элементы, например

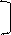
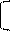1, 2, 3, 4, 5

2, 4, 1, 5, 3

Если поменять строки местами и упорядочить столбцы по возрастанию чисел в первой строке, то получим перестановку, называемую обратной. Для перестановки A обратная перестановка обозначается A^-1. В приведенном примере обратной будет перестановка

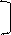
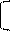1, 2, 3, 4, 5

3, 1, 5, 2, 4

Произведение перестановок C = A*B определяется следующим образом. Если в перестановке A на месте i находится элемент j, а в перестановке B на месте j элемент k, то в произведении C на месте i окажется k. Например,

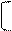
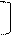
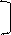
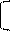1, 2, 3, 4, 5 1, 2, 3, 4, 5 1, 2, 3, 4, 5

2, 4, 5, 2, 1 * 5, 3, 1, 2, 4 = 3, 2, 4, 3, 5

Произведение перестановок некоммутативно, то есть A*B ≠ B*A.

Единичной называется перестановка (1, 2, …, n). Произведение как справа, так и слева любой перестановки на единичную не меняет ее, а произведение перестановки на обратную дает единичную перестановку. Таким образом, множество перестановок определенного порядка образуют группу.

В группе перетановок можно решить, например уравнение A*X = B, где A и B – заданные перестановки. Умножая обе части уравнения слева на A^-1, получим X = B* A^-1.

Распространенными задачами для перестановой являются генерация всех перестановок в определенном порядке и выбор случайной перестановки с равной вероятностью.

Начнем с задачи перечисления всех перестановок в лексикографическом порядке. Перестановка (α₁, α₂, …, α_n) считается лексикографически меньше перестановки (β₁, β₂, …, β_n), если α_i = β_i при i = 1, …, k и α_i < β_i при i = k + 1. Лексикографический порядок называют иногда алфавитным. Действительно, именно такой принцип лежит в основе расположения слов по алфавиту. Например, при n = 3 в лексикографическом порядке следуют перестановки (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Если рассматривать эти перестановки как трехзначные числа, то лексикографический порядок совпадает с расположением чисел по возрастанию.

Приведем алгоритм перечисления перестановок порядка n в лексикографическом порядке.

1. Выбор начальной перестановки π = (π₁, π₂, …, π_n) = (1, 2, …, n).

2. Выдача перестановки π.

3. Просмотр перестановки π справа налево. Поиск самой правой позиции i такой, что π_i< π_i+1. Если это невозможно, то конец перебора (выдана последняя наибольшая перестановка).

4. Поиск π_j – наименьшего элемента справа от π_i такого, что π_j> π_i.

5. Транспозиция (обмен) элементов π_j и π_i. В результате π_i+1 > π_i+2 > …> π_n.

6. Начиная с позиции i+1 изменение элементов перестановки на π_n, π_n-1,…, π_i+1. Переход к 2.

Пусть, например, последняя выданная перестановка π = (2, 6, 5, 8, 7, 4, 3, 1). Здесь n = 8, i = 3 и π_i =5, j = 5 и π_j =7. После транспозиции элементов π_j и π_i получается перестановка (2, 6, 7, 8, 5, 4, 3, 1), а после изменения мест конечных элементов приходим к следующей в лексикографическом порядке перестановке (2, 6, 7, 1, 3, 4, 5, 8).

Если перечислять перестановки порядка 5 с самого начала, то последовательно получим перестановки (1, 2, 3, 4, 5), (1, 2, 3, 5, 4), (1, 2, 4, 3, 5), (1, 2, 4, 5, 3) и т. д.

Дата добавления: 2014-01-11