Коды Грея

Подмножества множеств

Случайные перестановки

Имея какой-либо способ нумерации перестановок порядка n, легко получить случайную перестановку, ставя ее в соответствие случайному целому числу из диапазона от 0 до (n-1)! Например, это можно сделать на основе векоров инверсий, как уже рассматривалось выше. Однако в дополнение к задаче выбора, скажем, случайного целого от 0 до 52!-1 существует еще задача превращения этого числа в перестановку, что требует порядка n² операций.

Эффективный метод порождения случайных перестановок осуществляют последовательности из n-1 случайных транспозиций. Начиная с любой перестановки (π₁, π₂, …, π_n), элемент π_n переставляется с одним из элементов π₁, π₂, …, π_n, выбираемым случайно. Затем π_n-1 меняется местами с одним из элементов π₁, π₂, …, π_n-1, выбираемым случайно и т. д.

Для того, чтобы показать, что все n! перестановок равновероятны, воспользуемся индукцией. Для n=1 результат очевиден. Предположим, что алгоритм порождает случайные перестановки для n=k, то есть вероятность получения любой перестановки из k элементов составляет 1/k! Пусть при n=k+1 получена перестановка П=(π₁, π₂, …, π_k+1), в которой элемент k+1 оказался на месте j (1 ≤ j ≤ k+1). Поскольку на любом из этих k+1 мест элемент k+1 может быть в соответствии с алгоритмом с равной вероятностью, то вероятность перестановки

P(П) = P(π₁, π₂, …, π_j-1, k+1, π_j+1,…, π_k+1) = (1/k!)*P(π₁, π₂, …, π_j-1, π_j+1,…, π_k+1)=

=(1/k!)*1/(k+1) = 1/(k+1)!

Следовательно, утверждение справедливо при n=k+1, то есть алгоритм порождает любую перестановку с равной вероятностью.

Пусть имеется множество A={a₁, a₂, …, a_n}. Имеется 2ⁿ подмножеств этого множества. Действительно, каждый из элементов независимо от других может как входить, так и не входить в подмножество.

Порождение всех подмножеств эквивалентно порождению всех n-разрядных двоичных наборов: a_i принадлежит подмножеству множества A тогда и только тогда, когда i-й разряд равен 1. В свою очередь задача порождения случайного подмножества сводится к задаче порождения случайного двоичного набора длины n, то есть случайного числа в диапазоне от 0 до 2ⁿ – 1.

Наиболее очевидным способом порождения всех двоичных наборов длины n является счет в системе счисления с основанием 2. При этом два последовательных подмножества могут значительно отличаться друг от друга количеством и составом элементов, что соответствует появлению старшего разряда в очередном двоичном числе.

Наименьшим возможным изменением при переходе от одного подмножества к другому является добавление или удаление одного элемента множества. В терминах двоичных наборов это означает, что последовательные наборы должны различаться в одном разряде. Такие последовательности двоичных наборов известны как коды Грея. Более точно: n-разрядный код Грея есть упорядоченная циклическая последовательность из 2ⁿ n-разрядных наборов (кодовых слов), такая, что последовательные кодовые слова различаются в одном разряде. Обычно начальным кодовым словом считают (0, 0,…, 0), хотя на самом деле это несущественно, поскольку код циклический.

Существует много n-разрядных кодов Грея. Рассмотрим один из них. Предположим, что

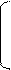G₀

G₁

G(n) = …

G_M,

где M = 2ⁿ -1, есть n-разрядный код Грея, записанный в виде матрица 2ⁿ × n так, что i-я строка матрицы является i-м кодовым словом. Тогда

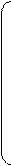
0G₀

0G₁

…

0G_M

G(n+1) = 1G_M

1G_M-1

…

1G₁

1G₀

очевидно, есть (n+1)-разрядный код Грея. По этому рекурсивному определению

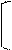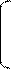
G(1) = 0

00

G(2) = 01

000

G(3) = 010

Можно определить (n+1)-разрядный код Грея иначе:

G₀0

G₀1

G₁1

G(n+1) = G₁0

G₂0

G₂1

…

…

Легко проверить, что таким образом получается тот же самый код Грея. Это рекурсивное определение близко к рекурсивному определению двоичного представления целых чисел. Действительно, если

0 B₀

1 B₁

2 B₂

… = …

… …

2ⁿ -1 B_M

то

0 B₀0

1 B₀1

2 B₁0

3 = B₁1

… …

2ⁿ⁺¹ -2 B_M0

2ⁿ⁺¹ -1 B_M1

Это позволяет предложить способ получения G_i из двоичного представления числа i. Если

i = (b_n b_n-1 …b₀)₂,

то

G_i = (g_n g_n-1 …g₁)₂,

где

g_j = b_j + b_j-1 (mod 2), 1 ≤ j ≤ n.

Последнее равенство дает возможность вычислить номер кодового слова G_i по его представлению. Пусть i = (b_n b_n-1 …b₀)₂. Тогда

_n

b_j = Σ g_m (mod 2), 1 ≤ j ≤ n.

^m=j+1

Сложение двух разрядов по модулю 2 то же самое, что исключающее “или” (XOR), поэтому можно просто сдвинуть разряды i на одну позицию влево и выполнить операцию исключающего “или”:

b_n b_n-1 … b₂ b₁ b₀

b_n b_n-1 b_n-2… b₁ b₀

g_n g_n-1 … g₂ g₁

Приведенные формулы позволяют перечислить нерекурсивно кодовые слова Грея заданной размерности n, изменяя i от 0 до 2ⁿ –1 и получая по двоичному представлению i разряды кодового слова G_i. Аналогично, если взять случайное число i в диапазоне от 0 до 2ⁿ –1, то по нему легко восстанавливается случайное кодовое слово G_i.

Пусть, например, n = 3, а i = 5 = (0101)₂. Тогда операция XOR дает:

0 1 0 1

0 1 0 1

1 1 1,

что соответствует кодовому слову G₅. В качестве проверки выполним обратное преобразование разрядов кодового слова G₅ в двоичные разряды i, в результате которого получим i = (0101)₂ = 5.

Дата добавления: 2014-01-11