Реляционные операторы

Операции над отношениями

Ключи отношений

· Значение кортежа t на атрибуте А называют t (А) или, другими словами, А - значение кортежа t.

· Если Х Ì R некоторого отношения, тогда t (Х) можно интерпретировать как вхождение кортежа t в атрибуты, определяемые множеством Х.

Среди атрибутов схемы отношений можно выбрать такое подмножество атрибутов К Ì R, что для любого t_i (K) будет выполняться t_i (K) ¹t_j (K), при i¹j.

· Если К - минимальное подмножество атрибутов из R, то К - ключ отношения.

· Отношение может иметь не единственный ключ. Эти ключи называют возможными ключами.

· Множество ключей, выбранных из всех возможных ключей и определенным образом перечисленных, называют выделенными ключами.

Один из выделенных ключей отношения выбирают в качестве первичного.

· Множество К Ì R называют суперключом, если К содержит любой из возможных ключей для r.

· Атрибут А называется первичным, если входит в состав любого из возможных ключей.

Замечание 1:

Конечные отношения могут иметь различные ключи в зависимости от значений и количества кортежей в отношении, но при этом схема отношения не меняется.

Замечание 2:

Понятие ключа задается для схемы отношения, но это необходимо делать с учетом всех возможных состояний отношений с данной схемой.

Манипулирование связями и сущностями может быть реализовано при помощи реляционной алгебры, которая задает операции над отношениями.

Теоретико-множественные операции над отношениями

Два отношения с одной и той же схемой могут быть рассмотрены как подмножества одного и того же множества, составленного из всех возможных кортежей с этой схемой.

Для такого представления могут выполняться теоретико-множественные операторы:

Если r и s со схемой R, то

q (R) = r È s- объединение;

q (R) = r Ç s- пересечение;

q (R) = r - s- вычитание;

r Ç s = r - (r - s).

Арность - размерность. Унарный - размерность 1, бинарный - размерность - 2, n - арный - размерность n.

Оператор выбора

· Выбор - унарная операция, результатом которой является новое отношение с набором кортежей, атрибуты которых удовлетворяют определенному условию:

s_F (r) = q

F - условное выражение, операндами которого являются имена атрибутов, связанных между собой логическими операциями или операциями сравнения.

Пример:

 

A1	A2	A3
а	б	в
a	е	а

r q

sF (r): (A1=a) È (A1 =a) A1	A2	A3
а	б	в
a	е	а
и	к	л

Оператор проекции

Это также унарный оператор над отношением. Отличие от “выбора” - этот оператор выбирает не кортежи, а столбцы.

r (R), XÌ R,

P_X (r) = q (X)

Если при этой операции образовались идентичные кортежи, то они удаляются. Операция проекции обладает свойством взаимопоглощения. Если две проекции выполняются последовательно и вторая операция выполняется по отношению к предыдущей операции, то конечный результат будет такой же, как непосредственно к исходному отношению, то есть

P_Y (P_X (r)) = P_Y (r)

Пример:

r (A, B, C)Х=(А,В); Y=(А)

A	B
а	б
d	е
и	к
а	б

а) r (A, B, C) П_Х (r) П_Y (r)

A а d и A	B	C
а	б	в
d	е	а
и	к	л
а	б	д

A

а

d

и

а

б) r (A, B, C) П_Y (r) П_Y (r)

A а d и A	B	C
а	б	в
d	е	а
и	к	л
а	б	д

Оператор декартова произведения

Это бинарный оператор, предназначенный для комбинирования двух отношений.

Пусть r₁ отношение арности к₁, r₂ - к₂.

· r = r₁ x r₂ будет представлять из себя множество кортежей арности к₁ + к₂ таких, что первые к₁ элементов кортежа отношения r составляют кортежи отношения r₁, а последующие к₂ элемента кортежа из r составляются кортежами из r₂. Сочетание кортежей из r₁ и r₂ при образовании кортежа r осуществляется по правилам декартова произведения.

Пример:

r₁ r₂ r = r₁ x r₂

а	р
с	и

а	б
с	d

а

б

а

р

а

б

с

и

с

d

а

р

с

d

с

и

Оператор естественного соединения отношений

Это бинарный оператор для комбинирования двух отношений.

Пусть r₁ (R₁) и r₂ (R₂), где

R₁ [A ₁, A ₂,..., A_K, B₁, B₂,..., B_n ]

R₂ [A ₁, A ₂,..., A_K, С₁, С₂,..., С_m ].

Тогда результатом естественного соединения будет отношение:

r = r₁ |> <| r₂=

= П

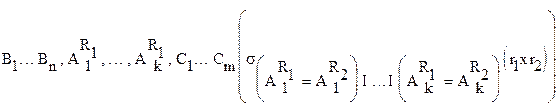
Пример:

1. r₁ r₂ 2. Сначала строим r = r₁ x r₂

		+ +   + + +

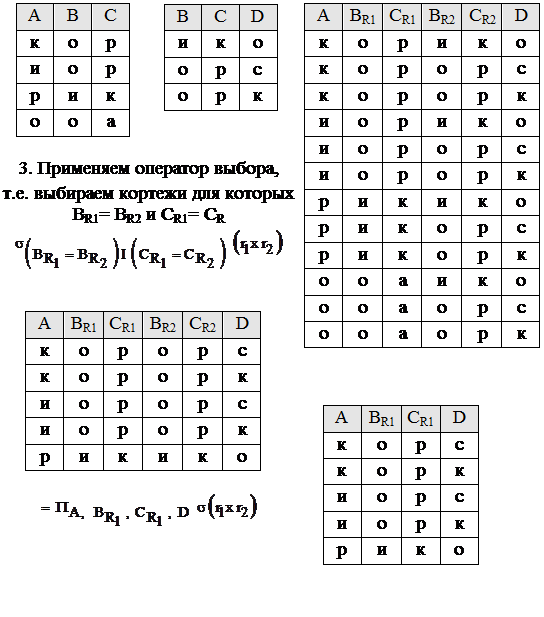Оператор соединения отношений

Пусть r (R) и s (S), где

R [A ₁, A ₂,..., A_k]

S [B₁, B₂,..., B_p].

Тогда оператор соединения отношений:

_{Ai Q Bj}

q(A ₁, A ₂,..., A_k, B₁, B₂,..., B_p) = r |> <| s = s _{Ai Q Bj} (r x s),

Q- оператор сравнения (=, >, <, ³, £, ¹)

Если Q - “=”, то соединение называется эквисоединением.

Пример:

А	В	С	D	E
а	б	с	а	и
а	б	с	е	к
а	и	р	а	и
а	и	р	е	к
о	е	ж	а	и
о	е	ж	е	к

1. r s 2. Строим r = r x s

		+

Оператор деления отношений

Пусть r (R) и s (S), где

R [A ₁, A ₂,..., A_k]

S [B₁, B₂,..., B_p] и B₁ º A_k-p+1,..., B_p º A_m. Знак º обозначает эквивалентность.

Тогда оператор:

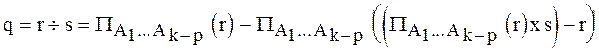
При этом q будет иметь схему отношений [A ₁, A ₂,..., A_k-p] и k>p.

Пример:

1. Есть r(A, B, C, D) и s (C, D) 2. П_А,В (r) 3. П_А,В (r) x s

А	В	C	D
и	о	с	а
и	о	р	к
о	р	с	а
о	р	р	к
с	к	с	а
с	к	р	к

А	В
и	о
о	р
с	к

А	В	С	D
и	о	р	к
о	р	с	а
с	к	р	к
и	о	с	а
с	к	с	а
и	о	к	с

C	D
с	а
р	к

	- - - + - -

4. П_А,В (r) x s - r 5. П_А,В (П_А,В(r) x s - r)

А	В	C	D
о	р	р	к

А	В
о	р

6. П_А,В (r) - П_А,В (П_А,В(r) x s - r) = r ¸ s

А	В
и	о
с	к

Замечание: Результатом деления является множество кортежей, полученных путем выделения начальных частей кортежей из r таких. что продолжением этого кортежа являются кортежи из s. деление может использоваться для поиска информации в БД о том, например, в каких подсистемах используются интересующие нас данные.

Дата добавления: 2014-01-11