Характеристическое уравнение

Из определения следует, что для нахождения собственного вектора необходимо решить систему

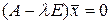, (2.4.4)

подобрав предварительно число . Для существования ненулевого решения системы (2.4.4) необходимо и достаточно, чтобы система была вырожденной. В этом случае определитель матрицы 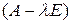равен нулю:

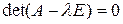, (2.4.5)

или 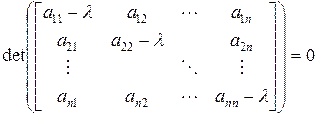. (2.4.6)

Раскрывая определитель, получим уравнение степени относительно :

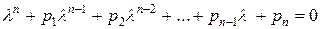. (2.4.7)

Уравнение (2.4.7) называется характеристическим уравнением. Левая часть уравнения называется характеристическим многочленом матрицы 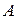. По основной теореме алгебры он имеет 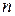корней (с учетом кратностей).

Пример 2.4.2. Пусть требуется, используя характеристическое уравнение, определить собственные числа матрицы

.

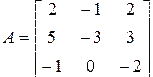Запишем характеристическое уравнение:

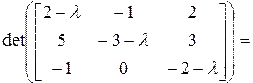
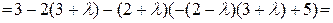
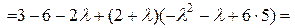
Решения характеристического уравнения: .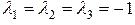

Можно проверить, что вектор

является собственным вектором.

Пример 2.4.3. Пусть требуется, используя характеристическое уравнение, определить собственные числа матрицы

.

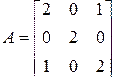Запишем характеристическое уравнение:

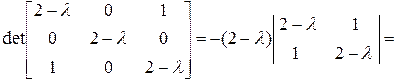
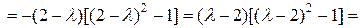
Решения характеристического уравнения: ; ; .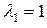

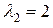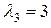Можно проверить, что соответственно векторы

; ;

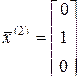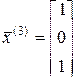
являются собственными по отношению к указанным собственным числам.

Как видно, в частности, из приведенных примеров число собственных векторов матрицы порядка 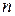не всегда равно 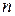. Матрицы, у которых число собственных векторов совпадает с порядком матрицы, называются диагонализируемыми. Диагонализируемыми, например, являются все симметричные матрицы. Матрицы, у которых число собственных вектором меньше, чем порядок матрицы, дефектными (это возникает в некоторых ситуациях при наличии кратных собственных чисел).

Отметим, что если – собственный вектор, то – также является собственным вектором, т.к. 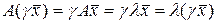. Иными словами, собственный вектор определен с точностью до множителя.

Рассмотрим произвольную диагонализируемую матрицу 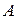. Пусть 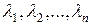– собственные числа матрицы 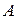, им соответствуют собственные вектора 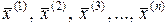, т.е.

.

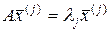Поскольку собственный вектор 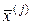определен с точностью до множителя, то всегда можно умножить его на число 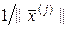, т.е. нормировать. Для нормированного вектора 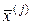справедливо равенство:

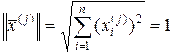. (2.4.8)

Кроме того, векторы 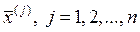образуют базис в 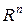, т.е. любой вектор 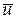может быть представлен в виде их линейной комбинации

. (2.4.9)

Заметим также, что

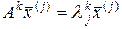. (2.4.10)

Дата добавления: 2014-01-11