Одноканальна система масового обслуговування

Вступ

У виробничих умовах дуже часто виникають ситуації, що можна інтерпретувати як потреби в обслуговуванні. Наприклад, при обслугуванні технологічних ліній ремонтними бригадами, при визначені показників надійності роботи устаткування, при визначені можливості підвищення продуктивності виробництва, тощо. У повсякденному житті до систем масового обслуговування належать телефонні та автозаправні станції, майстерні та ін. У таких системах є два потоки: потік замовлень та вихідний потік обслугування. Якщо інтенсивність обслугування мала, утворюється черга, яку можна скоротити, якщо використати декілька каналів обслуговування.

Системи масового обслуговування (СМО) призначені для обслуговування потоку замовлень або вимог, що надходять у випадкові моменти часу. Кожна СМО складається з деякого числа каналів обслуговування, якими, в залежності від виду системи, можуть бути технологічні лінії, лінії зв’язку, робочі точки чи агрегати, під’їздні шляхи, ремонтні бригади, тощо. Виконання замовлення, що надходить у систему, тобто її обслугування, продовжується деякий випадковий час, після чого канал звільняється і готовий прийняти наступне замовлення.

Теорія СМО вперше була розроблена датським математиком Ерлангом стосовно до запитів, що надходили на телефонну станцію. Тому основні поняття і визначення зберігаються з практики забезпечення телефонної мережі.

Замовлення, що надходять на вхід СМО утворюють неперервний потік подій. Не завжди заздалегідь можливо передбачити, коли надійде замовлення, але якщо розглядати усі замовлення, то, незважаючи на випадковий характер кожної події, будемо визначати інтенсивність потоку замовлень l як середнє число замовлень у одиницю часу. Наприклад, за 1 годину відбулося 12 замовлень, отже, в середньому, одне замовлення приходиться на інтервал у 60/12=5 хвилин. Таким чином,інтенсивність потоку l = 1/5 = 0.2.

Простіші потоки, у яких інтенсивність є постійною величиною (l=const), називаються стаціонарними.

СМО бувають двох типів:

- СМО з відмовами, у яких замовлення, що надійшло у той момент, коли усі канали зайняті, отримує відмову і не обслуговується;

- СМО з очікуванням, у яких кожне замовлення, що надійшло у систему, коли немає вільних каналів, залишається у черзі і очікує, поки звільниться якийсь канал і візьме її на обслугування.

Порядок обслугування черги не обов’язково підпорядкований принципу: першим прийшов – першим обслуговується, у виробничих умовах часто буває навпаки: в першу чергу обслуговуються деталі, що надійшли останніми, оскільки саме вони лежать у бункері зверху. Деколи замовлення обслуговуються у випадковому порядку.

2. Використання теорії масового обслуговування у керуванні виробництвом

Для того, щоб зрозуміти, як роз’язуються задачі управління виробництвом з використанням ТМО, розглянемо її основи за допомогою прикладів.

2.1. Системи масового обслуговування з відмовами

Нехай виробнича система складається з двох пристроїв, які виробляють одну і ту ж продукцію. Пристрої в ході роботи можуть виходити з ладу (відмовляти). Пристрій, що відмовляє, відразу починає ремонтуватись. Така система має чотири стани:

- Стан S1 - обидва пристрої працюють;

- Стан S2 - перший пристрій ремонтується (після відмови), другий працює;

- Стан S3 - другий пристрій ремонтується, перший працює;

- Стан S4 - обидва пристрої ремонтуються.

Позначимо l1 – інтенсивність потоку відмов першого пристрою; l2 – інтенсивність потоку відмов другого пристрою. m1 – інтенсивність потоку закінчень ремонтів першого пристрою; m2 – інтенсивність потоку закінчень ремонтів другого пристрою.

Граф станів такої виробничої системи наведений на рис.1.

l1

m1

S3

S1

S2

S4

m2 l2 m2 l2

l1

m1

Рис.1. Граф станів виробничої системи

Переходи S1®S2; S1®S3; S2®S4; S3®S4 здійснюються в результаті відмов у системі. Зворотні переходи є наслідком ремонтних робіт. Відмови і закінчення ремонтів – випадкові величини.

Нехай мається N однакових систем, які описуються наведеним графом станів (N>>1). Число систем, що знаходиться у стані Si, дорівнює N×p_i, де p_i – ймовірність перебування системи у стані Si (це твердження тим точніше, чим більше N). Розглянемо конкретний стан, наприклад, S1. З цього стану можливі переходи у стани S2 і S3 – з сумарною ймовірністю l1+l2, що віднесена до одиниці часу. У стаціонарному режимі інтенсивність потоку дорівнює ймовірності за кінцевий проміжок часу, поділений на цей проміжок часу.

Розглянемо виходи із стану S1. Враховуючи вищенаведене, число виходів із стану S1 за одиницю часу у колективі систем, що розгядаються, дорівнює:

N*p₁ ×(l1+l2).

Загальне правило: число переходів із стану і у стан j (Si®Sj), що здійснюється за одиницю часу дорівнює добутку кількості систем у стані Si помножене на ймовірність переходу, за одиницю часу.

Входи у стан S1 (рис. 1) здійснюються із станів S2 і S3. Число входів у S1 за одиницю часу становить N*p₂ + N*p₃. Оскільки розглядається стаціонарний процес, то числа виходів і входів для кожного із станів мають бути збалансованими. Отже для стану S1 маємо рівняння балансу:

N×p₁×(l1+l2)=N×p₂×m1 + N * p₃×m2. (1.1)

Розглянемо баланс входів і виходів для кожного стану і, скорочуючи у рівняннях загальний множник N, отримуємо такі рівняння відносно ймовірностей p1, p2, p3, p4.

Для стану S1:

p₁×(l1+l2)=p₂×m1+p₃×m2 (1.2)

Для стану S2:

p₂×(l1+m1) = p₁ ×l1 + p₄ ×m2 (1.3)

Для стану S3:

p₃×(l1+m2) = p₁ ×l2 + p₄ ×m1 (1.4)

Для стану S4:

p₄×(m1+m2) = p₂ ×l2 + p₃ ×l1 (1.5)

Неважко переконатися, що четверте рівняння може бути отримано як сума перших трьох. Замість цього рівняння скористаємося рівнянням р₁+р ₂ +р₃+р₄ = 1, що означає, що система з достовірністю знаходиться в будь-якому з чотирьох станів. Таким чином, приходимо до системи рівнянь:

p₁×(l1+l2) = p₂ ×m1 + p₃ ×m2

p₂×(l1+m1)=p₁×l1+p₄×m2 (1.6)

p₃×(l1+m2) = p₁ ×l2 + p₄ ×m1

р₁+р₂+р₃+р₄ = 1

Система (1.6) називається системою рівнянь Колмогорова. Вона дозволяє обчислювати ймовірності знаходження системи у кожному з визначених станів. В теорії потоків, коли швидкість переходу з одного стану в інший є великою, процес функціонування системи описується рівняннями Колмогорова.

Розглянемо систему масового обслугування з відмовами.

Найпростіший приклад системи масового обслуговування з відмовами є автоматична телефонна станція. Якщо абонент, що викликається, зайнятий, даються короткі гудки, очікування безглузде. В залежності від ступеня необхідності обслугування, замовлення або залишають систему, або повертаються повторно.

Одноканальна система масового обслуговування – це найпростіша СМО, за допомогою якої можна розглянути деякі закономірності управління виробництвом.

На вхід одноканальної системи, що має один канал обслуговування, надходить потік замовлень з інтенсивністю l. Замовлення, що надійшло у момент, коли система вільна, відразу ж починає обслуговуватись. Наступне замовлення, яке надходить коли канал обслугування зайнятий, отримує відмову (рис.2). Час обслугування замовлення є випадковим, але на виході створюється потік обслугування з інтенсивністю m, що визначається середнім часом обслуговування.

Наприклад, якщо середній час обслугування одного замовлення складає 0.2 хвилини, то інтенсивність потоку обслугування m = 1 / 0.2 = 5.

Станція

Потік замовлень Потік обслугування

Рис 2. Потік замовлень і потік обслугування в системі масового обслугування.

Одноканальна СМО може знаходитися лише в одному з двох станів: S0- канал вільний, S1 – канал зайнятий. Граф станів імовірних переходів із одного стану в інший наведений на рис. 3.

l

S1

S0

m

Рис.3. Граф одноканальної СМО з відмовами.

Позначимо - р₀ ймовірність знаходження СМО у стані S0. Відповідно р₁ – ймовірність того, що система знаходиться у стані S1. Оскільки система завжди знаходиться в одному з двох станів, то сума імовірностей дорівнює 1:

p₀+р₁ = 1.

Дії, що виводять її із стану S0 мають врівноважуватися діями, що повертають систему в стан S0, отже

l×р₀ = m×р₁.

З цього виразу визначаємо

р₁=(l× p₀ ) / m

Враховуючи, що сума імовірностей завжди дорівнює 1, отримуємо

р₀+(l×р₀)/ m=1

Отже,

p₀=1/(1+l/m)=m/(l+m) (1.7)

І відповідно,

p₁ = l¤m×p₀ = l¤(l+m). (1.8)

Основні показники СМО з відмовами: відносна пропускна здатність, абсолютна пропускна здатність, а також ймовірність отримання відмови.

Відносна пропускна здатність q визначається ймовірністю того, що в момент надходження замовлення канал вільний і воно буде обслуговуватись, тобто для одноканальної системи q = p₀. У границі, коли вже процес установився, значення відносної пропускної здатності СМО буде дорівнювати

Q = m ¤ (l + m) (1.9)

Абсолютна пропускна здатність А визначається добутком відносної пропускної здатності на інтенсивність потоку замовлень.: А = q× l. У границі вона стає рівною:

A = l × m ¤ (l + m). (1.10)

Ймовірність того, що замовлення буде обслуженим, визначається р₀, а імовірність отримання відмови – р₁. Таким чином,

P_{відмови}=p₁=l¤(l+m) (1.11)

2.1.2. Багатоканальні системи масового обслуговування

Багатоканальні системи масового обслуговування використовуються для підвищення пропускної спроможності СМО (наприклад збільшується число ліній зв’язку в телефонній мережі або кількість контрольних приладів на виробництві, тощо).

На перший погляд, чим більшу кількість каналів ми встановимо, тим краще і зручніше для користувача, але загальна ефективність системи при цьому може знизитись, оскільки кожний новий канал потребує додаткових витрат на встановлення та обслуговування.

Граф двоканальної системи масового обслуговування з відмовами буде мати вигляд, наведений на рис 4.

l l

m 2m

Рис.4. Граф двоканальної системи масового обслуговування.

Стан S0 –обидва канали вільні, стан S1 - в СМО є одне замовлення і один канал зайнятий, а другий вільний, стан S2 – обидва канали зайняті обслугуванням замовлень і наступним замовленням буде даватися відмова. Із стану S0 у стан S1 систему переводить потік замовлень з інтенсивністю l. Як тільки надходить перше замовлення, один канал стає зайнятим, той же потік з інтенсивністю l переводить СМО з першого стану у другий, коли зайняті обидва канали.

Якщо у системі зайнятий один канал (стан S1), то цей канал здійснює m обслуговувань за одиницю часу. Тепер нехай система знаходиться у стані S2, тобто в ній працюють два канали. У стан S1 система буде переходити, якщо обслугування закінчив або перший, або другий канал. Таким чином, сумарна інтенсивність потоку обслугування буде дорівнювати 2×m.

Для стану S0 баланс дій буде:.

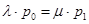
(1.12)

Звідси отримуємо:

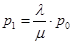(1.13)

Для стану S1 баланс дій визначається:

З урахуванням того, що m р₁ = l р₀ (з 1.12), отримуємо

2 ×m ×р₂ = l× р_1,

або інакше

(1.14)

Оскільки сума усіх імовірностей має дорівнювати 1, отримуємо

Звідси витікає:

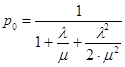(1.15)

Граф станів трьохканальної системи масового обслуговування з відмовами має вигляд, наведений на рис.5.

S3

S2

S1

S0

l l l

m 2m 3m

Рис.5. Граф трьохканальної СМО з відмовами.

Повторимо висновки, аналогічні попереднім, за формулами 1.12-1.15 отримуємо для стану S2 баланс дій:

l×р₂ +2×m×р₂ = l×р₁ +3×m×р₃ (1.16)

Звідси

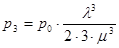(1.17)

Якщо сума ймовірностей дорівнює 1, то

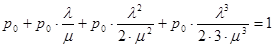
Звідси

(1.18)

Таким чином, для n-канальної системи масового обслуговування з відмовами граф станів має вигля, наведений на рис.6.

Sn

S3

S2

S1

S0

l l l l l

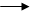
m 2×m 3×m 4×m n×m

Рис.6. Граф станів багатоканальної СМО.

Такою ж процедурою, що здійснювалась для 2- та 3- канальних СМО, можна отримати ймовірність перебування системи у кожному стані j (j=1,…n):

(1.20)
Ймовірність того, що всі канали вільні:

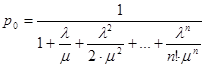(1.21)

Ймовірність відмови (тобто ймовірність того, що усі канали зайняті) дорівнює p_n, а відносна пропускна здібність такої системи:

q = 1 - p_n.

Звичайно, чим більша кількість каналів, тим вища ймовірність обслугування, але при цьому може знизитися ефективність роботи системи із-за простою у цих каналах та зайвих витрат на їх обслугування.

Для багатоканальних СМО вводиться ще один параметр – середнє число зайнятих каналів:

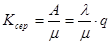(1.16)

2.2. Системи масового обслугування з очікуванням.

Розглянемо СМО з одним каналом, на вхід якого надходять замовлення з інтенсивністю l. Замовлення, що надішло у момент, коли канал зайнятий, стає у чергу і очікує. Граф станів такої системи наведений на рис 7.

l l l l

Sk

S2

S1

S0

m m m m

Рис.7. Граф системи масового обслугування з очікуванням.

Стан S0 відповідає вільному каналу; S1 - канал зайнятий і черги немає; S2 - канал зайнятий і одне замовлення знаходиться у черзі; S3 – у черзі два замовлення і т.д. У стані Sk - канал зайнятий і у черзі к-1 замовлення. За стрілками зліва направо систему з одного стану в інший переводить потік замовлень з інтенсивністю l, а за стрілками справа наліво - потік обслуговувань, що має інтенсивність m. Кожного разу при переході з одного стану в інший черга змінюється на одиницю.

Для визначення ймовірності початкового стану можна використати рівняння (1.12):

l×р₀ = m×р₁.

Звідси

р₁=(l/m)×p₀.

Величину r=l/m (1.22)
називають інтенсивністю навантаження СМО.

Для стійкої роботи СМО з очікуванням необхідно, щоб середня інтенсивність потоку обслугування була більше інтенсивності потоку замовлень, тобто l < m, отже r < 1. Якщо l > m, система не впорається з обслуговуванням і черга буде зростати до нескінченності.

Використовуючи введені позначення та формули (1.12),(1.22), ймовірність стану S1 можна записати у вигляді:

р₁=r×p₀ (1.23)

Щоб отримати ймовірності p₂ i p₃,…,p_k можна використати отримані раніше вирази для стану S1:

l×p₁+m×p₁=l×p₀+m×p₂

Оскільки l×p₀=m×p₁ та m×p₂=l×p₁

Отже p₂=p₁×l¤m = r² ×p₀.

Аналогічно для стану S2: p₃ = r³ ×p₀. І.т.д.

p_k=r^k×p₀. (1.24)
Для визначення р₀ запишемо вираз для суми ймовірностей:

p₀ + r ×p₀ + r² ×p₀ +…+ r^k ×p₀ = 1.

Ліва частина останнього виразу є сумою членів геометричної прогресії, тому вона дорівнює 1/(1- r). Тому p₀ = 1 - r, звідси отримуємо

p_k=r^k×(1-r) (1.25)

Використовуючи цей вираз, можна визначити характеристики СМО з очікуванням, важливі для її функціонування: середню довжину черги Lq, середнє число замовлень в системі Ls, середній час перебування замовлення в системі Ws, середня тривалість очікування замовлення у черзі Wq і імовірність утворення черги р_к.

З ймовірністю p₂ у черзі знаходиться одне замовлення, з ймовірністю p₃ – два замовлення, і з імовірністю p_k у черзі – (k-1) замовлення.

Отже,

Lq=1× p₂ +2× p₃ +…+(k-1)×p_k=r²×(1-r)×(1+2×r+3×r²+…+k×r^k-1).

Cума геометричної прогресії 1+2×r+3×r²+…+k×r^k-1=

=1/(1-r)².

Тому середня довжина черги:

(1.26)

Середня кількість замовлень, що знаходиться у системі обслугування - Ls, складається з середньої кількості замовлень у черзі та середньої кількості замовлень на обслуговуванні (включаючи інтервали, коли черги не було).

Ls=0×p₀+1×p₁+2×p₂+…+ k×p_k

Ця величина приймає значення 0, коли канал вільний, імовірність такого стану дорівнює p₀ = 1 - r.

Якщо канал зайнятий і одне замовлення обслуговуються Ls = 1, ймовірність такої події: p₁=1 – p₀ = r.

Отже,

(1.27)

Середній час очікування у черзі дорівнює середньому числу замовлень у черзі, поділеному на інтенсивність потоку обслуговування.

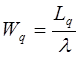
або

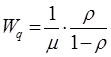(1.28)

Імовірність утворення черги дорівнює імовірності того, що у системі буде більше однієї вимоги, тобто:

Pk=1–p₀–p₁=1–(1-r)-r(1 - r) = r² (1.29)

Середній час перебування замовлення у черзі
або (1.30)

3. Практичне застосування теорії масового обслуговування.

Дата добавления: 2014-01-11