
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод равномерной оптимизации
|
|
|
|
Методика выбора оптимального бизнес-проекта (электронного магазина) на основе многоцелевой оптимизации
Методика выбора оптимального бизнес-проекта (электронного магазина) на основе многоцелевой оптимизации
Первоначальную основу любой методики составляет экономико-математическая модель (ЭММ) решения задачи. Поэтому разработаем ЭММ задачи обоснования выбора из альтернативных бизнес-проектов экономически наиболее эффективного (оптимального). Как было доказано выше, ЭММ должна быть многокритериальной (многоцелевой). В качестве критериев оптимальности ЭММ рекомендуются наиболее часто используемые (согласно имеющейся статистике) в соответствующих расчетах показатели чистой приведенной стоимости (ЧПС), индекса рентабельности (ИР) и дисконтированного срока окупаемости (ДСО) капитальных вложений.
Экономико-математическая модель задачи выбора оптимального варианта бизнес-проекта создания электронного магазина.[15]
С целью формализации задачи введем необходимые обозначения: i — код целевой функции (1=1,...,n);
j— номер альтернативного варианта бизнес-проекта (j = 1,...,m);
{хj} — множество j-x вариантов бизнес-проектов;
Xj — оптимальный вариант бизнес-проекта.
Необходимо выбрать из некоторого множества {хj} альтернативных бизнес-проектов оптимальный вариант Xj; который удовлетворял бы следующим основным условиям:
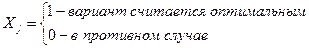 (1)
(1)
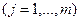
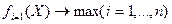 (2)
(2)
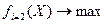
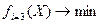
Неравенство (1) отражает те значения целочисленной переменной, которые могут принимать участвующие в экономической экспертизе бизнес-проекта.
Целевая функция (2) характеризует требование максимизации величины показателя ЧПС по искомому варианту бизнес-проекта.
Целевая функция (3) отражает требование максимизации величины показателя ИР по искомому варианту бизнес-проекта.
Целевая функция (4) предусматривает необходимость обеспечение минимального ДСО по искомому варианту бизнес-проекта.
Как видим, ЭММ является многоцелевой и требует использование соответствующего математического аппарата для своего решения.
Наиболее часто в качестве критериев оптимальности рекомендуется один из следующих критериев: ЧПС, ИР и ДСО. Отдать предпочтение какому-либо из них весьма затруднительно, так как каждый из ни имеет свои достоинства и недостатки.
Основные достоинства и недостатки указанных критериев и соответствующих им методов расчета приведены в табл. 21.6-21.8.
Отмеченные недостатки, свойственные методу определения ЧПС обусловливают необходимость применения его в сочетании с другими методами.
Как видим, каждый из приведенных выше трех методов характеризуется рядом достоинств и существенных недостатков. Отдать безусловное предпочтение какому-либо одному методу не представляется возможным. В случае применения многоцелевого подхода отпадает необходимость решения этой проблемы. Он предусматривает одновременное их применение при обосновании выбора наиболее эффективного варианта бизнес-проекта.
Таблица 21.6
Достоинства и недостатки метода, основу которого составляет расчет ЧПС
| Достоинства | Недостатки |
| 1 Сравнительная простота расчетов | 1. Достаточно большая по объему величина ЧПС не всегда соответствует экономически целесообразному варианту капиталовложений |
| 2. Непротиворечивый характер критерия, позволяющий осуществлять достоверное ранжирование проектов в порядке убывания (возрастания) экономического эффекта | 2. При достаточно высоком уровне дисконтной ставки (цены капитала) отдельные денежные потоки оказывают сравнительно малое влияние на объем ЧПС |
| 3. Наилучшим образом характеризует уровень отдачи на вложенный капитал | 3. Критерий мало пригоден для сравнения инвестиционных проектов с примерно одинаковыми объемами ЧПС, но со значительно разной капиталоемкостью |
Таблица 21.7
Достоинства и недостатки метода, основу которого составляет расчет индекса рентабельности
| Достоинства | Недостатки |
| 1. Достаточная простота расчетов | 1. Не учитывает денежные потоки, находящиеся за пределами срока окупаемости вложений |
| 2. Удобен для использования в фирмах с небольшим денежным оборотом, а также для получения быстрой оценки результатов расчетов в случае недостатка ресурсов | 2. Наличие субъективности при установлении нормативного (желаемого) срока окупаемости инвестиций, с которым впоследствии сравнивается расчетный срок окупаемости |
| - | 3. Не пригоден к применению для проектов с одинаковыми сроками окупаемости, но с весьма различными жизненными циклами (периодами реализации) |
| - | 4. Присутствие жесткой зависимости точности результатов расчетов от частот разбиения жизненного цикла бизнес-проектов на дифференцированные периоды их реализации (полугодия, кварталы) |
| - | 5. Возможность получения лишь весьма приближенной оценки уровня риска инвестиций |
| - | 6. Ограничение ролью дополнительного метода оценки эффективности альтернативных проектов |
Проиллюстрируем суть предлагаемой многоцелевой методики расчетов на условном примере.
Пусть имеется 10 альтернативных бизнес-проектов создания электронного магазина с заданными параметрами, из которых необходимо выбрать один оптимальный. Для каждого из бизнес-проектов путем последовательных расчетов были определены соответствующие им численные значения критериев ЧПС, ИР и ДСО. Результаты этих расчетов приведены в табл. 2.8.
Выбор из 10 вариантов бизнес-проектов оптимального легко осуществить в том случае, если в качестве абсолютно доминирующего принять какой-то один критерий оптимальности. В РФ согласно действующей официальной методике предпочтение отдается критерию ЧПС. В таком случае оптимальным следовало бы признать 10-й вариант бизнес-проекта. Однако, если эксперт-профессионал по инвестициям одновременно учтет числовые оценки всех трех критериев, то этот вариант окажется далеко не оптимальным, о чем убедительно свидетельствуют выполненные ниже расчеты.
Таким образом, достоверный выбор экономически наиболее эффективного варианта бизнес-проекта должен осуществляться, как это было аргументировано выше, на основе многоцелевого подхода. Проведем экономическую экспертизу альтернативных бизнес-проектов, предусматривающих создание некоторого электронного магазина, с помощью ряда математических методов.
В связи с тем, что критерии оптимальности ЧПС, ИР, ДСО имеют разную экономическую природу и неодинаковые единицы измерения, первым шагом должна являться процедура их нормализации по приведенной выше формуле (т. е. приведение к безразмерным величинам).
Таблица 21.8
Результаты расчетов численных значений ЧПС, ИР и ДСО по альтернативным вариантам бизнес-проектов
| Номер варианта (j) | ЧПС 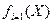 , тыс. руб. , тыс. руб.
| ИР
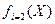
| ДСДСО 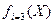 , год , год
|
| 1,20 | 2,5 | ||
| 1,22 | 2,6 | ||
| 1,24 | 2,4 | ||
| 1,26 | 2,3 | ||
| 1,23 | 2,7 | ||
| 1,22 | 2,8 | ||
| 1,21 | 3,1 | ||
| 1,20 | 3,0 | ||
| 1,18 | 2,6 | ||
| 1,19 | 2,6 |
В качестве иллюстрации выполним необходимые расчеты с целью получения нормализованных значений трех критериев по первому варианту бизнес-проекта:
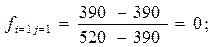
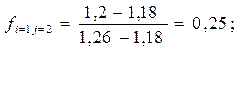
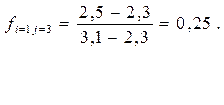
Итоговые результаты расчетов по всем бизнес-проектам приведем в табл. 20.9.
Из ЭММ рассматриваемой задачи видно, что критерий оптимальности под номером три минимизируется, а первые два максимизируются. Для упрощения расчетов умножим безразмерные величины третьего критерия на -1 (минус единицу) с целью обеспечения единого направления оптимизации, т. е. максимизации. В сводном виде результаты расчетов приведены в табл. 21.10.
Таблица 21.9
Результаты расчетов нормализованных значений критериев оптимальности по альтернативным бизнес-проектам
| Номер варианта (j) | Безразмерные величины критериев оптимальности | ||
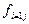
| 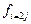
| 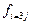
| |
| 0,25 | 0,25 | ||
| 0,0769 | 0,5 | 0,375 | |
| 0,1538 | 0,75 | 0,125 | |
| 0,2308 | |||
| 0,3846 | 0,625 | 0,5 | |
| 0,4615 | 0,5 | 0,625 | |
| 0,6154 | 0,375 | ||
| 0,7692 | 0,25 | 0,875 | |
| 0,8462 | 0,375 | ||
| 0,125 | 0,5 |
Решим задачу поиска оптимального варианта бизнес-проекта из множества альтернативных различными математическими методами.
Исходной посылкой (принципом) данного метода является то, что все критерии оптимальности считаются экономически равноценными. Согласно этому методу лучшим считается вариант, у которого суммарная величина всех числовых значений целевых функций принимает максимальное значение:
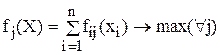 .
.
На основании данных табл. 6.1 1 получим:
mах{0 + 0,25 - 0,25 = 0; 0,0769 + 0,5 - 0,375 = 0,2019;
0,1538 + 0,75 - 0,125 = 0,7788; 0,2308 + 1 - 0 = 1,2308;
0,3846 + 0,625 - 0,5 = 0,5096; 0,4615 + 0,5 - 0,625 = 0,3365;
0,6154 + 0,375 - 1 = -0,0096; 0,7692 + 0,25 - 0,875 = 0,1442;
0,8462 + 0 - 0,375 = 0,4712; 1 + 0,125 - 0,5 = 0,675}.
Таблица 21.10
Численные значения критериев с одинаковым направлением оптимизации
| Номер варианта (j) | Безразмерные величины используемых критериев оптимальности | ||
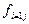
| 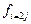
| 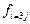
| |
| 0,25 | -0,25 | ||
| 0,0769 | 0,50 | -0,375 | |
| 0,1538 | 0,75 | -0,125 | |
| 0,2308 | |||
| 0,3846 | 0,625 | -0,5 | |
| 0,4615 | 0,5 | -0,625 | |
| 0,6154 | 0,375 | -1 | |
| 0,7692 | 0,25 | -0,875 | |
| 0,8462 | -0,375 | ||
| 0,125 | -0,5 |
Из приведенных расчетов следует, что экономически наиболее эффективным является четвертый вариант. Для большей наглядности сведем расчетные данные в табл. 21.11.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2291; Нарушение авторских прав?; Мы поможем в написании вашей работы!