Основы статистического вывода

Статистический вывод – это область статистической науки, позволяющая делать выводы о неизвестных характеристиках и свойствах генеральной совокупности на основании результатов выборочного исследования.

??? Основные задачи:

1. Оценивание неизвестных параметров генеральной совокупности.

2. статистическая проверка гипотез по генеральной совокупности.

Основой статистического вывода является применение случайного отбора (т.е. используются выборки, построенные случайным образом).

Все формулы в рамках данного курса строятся на предположении об использовании простой случайной выборки.

Параметрами генеральной совокупности являются все её количественные характеристики. Аналогичные характеристики выборки называются выборочными статистиками.

В некоторых случаях параметры и выборочные характеристики, измеряющие одно и то же, имеют разные названия и обозначения.

Простая случайная выборка - это выборка, построенная по следящим правилам:

1. Используется полный список генеральной совокупности.

2. к этому списку применяется одна из процедур простого случайного отбора:

a. лотерея

b. таблица случайных чисел (применяется, когда генеральная совокупность велика для лотереи).

c. Компьютерные датчики случайных чисел.

! Основной недостаток простого случайного отбора – неодинаковая доступность элементов для исследования.

Простой случайный отбор – самый сложный вид выборки для извлечения и использования (однако математические формулы проще).

Основные понятия теории вероятности.

Теория вероятности является методологической основой математической и прикладной статистки. Применяется, когда необходимо описать бесконечную генеральную совокупность.

Понятия:

1. Случайная величина.

2. Выборочное пространство.

3. Случайное событие.

4. Вероятность случайного события.

5. Аддетивность вероятности.

Случайная величина – это функция, которая служит для измерения какого-либо качества у элементов генеральной совокупности, и принимает на каждом элементе совокупности некоторое значение. (X,Y,Z).

! Существенное отличие от переменных (характеризующих выборку): случайные величины бывают только количественными.

! случайные величины бывают дискретными и непрерывными.

Выборочное пространство – это множество всех возможных значений случайной величины. (S).

Пример:

IQ S= {40, 41, 42, …, …, 160}

Рост S= {140; 220}

Для дискретных величин – это набор значений, для непрерывных – интервал.

Случайное событие – это любое подмножество выборочного пространства (!!! для непрерывных случайных величин событие может быть только интервалом). (E).

Для удобства математических манипуляций используют две абстракции:

1. полное случайное событие (которое совпадает с выборочным пространством).

2. пустое случайное событие {Ø} (никаких значений случайной величины).

Для непрерывной случайной величины отдельное значение не является событием. В данном случае событием могут быть только интервалы:

E₁≠ {170};

E₁= (140; 141);

E₂= (141; 142).

! В данном случае форма скобки не имеет принципиального значения, потому что отдельное значение (тут 141) событием не является.

Пересечение интервалов непрерывной СВ считается пустым, т.к. отдельное значении такой СВ – не событие:

E₁= [140; 150]

E₂= [150; 160]

! В данном случае 150 – не пересечение, т.к. не является событием.

Вероятность случайного события – это относительная частота объектов из генеральной совокупности, относящихся к данному событию. (P).

! Для непрерывных случайных величин вероятность для отдельного значения не вычисляется.

Аддитивность вероятности – это свойство вероятности быть складываемой при определенных условиях: при непересекающихся случайных событиях.

!!!! Если случайные события не пересекаются, вероятность отнесения объекта к одному из них равна сумме вероятностей данных событий:

(E1∩E2 = Ø) & (E2∩E3 = Ø) & (E1∩E3 = Ø) =>

=>

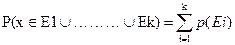
Предельный случай аддитивности вероятности: если случайные события не пересекаются и перекрывают всё выборочное пространство, то сумма вероятностей этих событий равна

(E1∩E2 = Ø) & (E2∩E3 = Ø) & (E1∩E3 = Ø) … … …

E1 U E2 U U … … U Ek = S => =1

Распределение случайной величины.

– это инструмент описания генеральной совокупности с точки зрения вероятности непересекающихся событий, перекрывающих всё выборочное пространство.

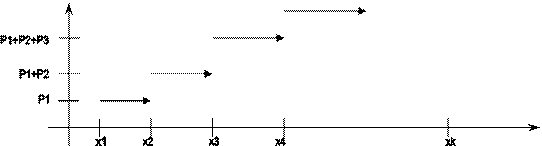
Распределение дискретной СВ задается перечислением её значений и соответствующих вероятностей.

X	X1	X2	X3	…	Xk	∑
	P1	P2	P3	…	Pk

Для решения задачи с P(x<a):

Если a < x min, то P(x<a) = 0.

Если x min < a < x max, то P(x<a) = .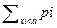

Если a > x max, то P(x<a) = 1.

Для решения задачи с P(x < a):

Если a < x min, то P(x < a) = 1

Если x min < a < x max, то P(x < a) =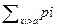

Если a > x max, то P(x < a) = 0.

Для решения задачи с P(a < x < b):

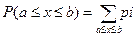, как для нестрогого неравенства.

Xi								∑
Fi
pi	0,08	0,19	0,24	0,16	0,08	0,14	0,08

P (x <4) = 0

P (x ≤ 4) = 0,08

P (x > 8) = 0,22

P (6 ≤ x ≤ 8) = 0,48

P (6 < x < 8) = 0,16

Свойства дискретного распределения:

1) 0 ≤ px ≤ 1 (вероятность любого значения изменяется от 0 до 1).

2) (сумма вероятностей для всех действительных чисел от - ∞ до + ∞ равна единице).

3) Вероятность того, что x лежит в интервале от а до b, равна сумме вероятностей:

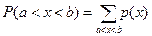
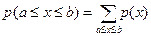
4)

Функция распределения F(a) = p (x ≤ a)

Определена как для непрерывных, так и для дискретных случайных величин – это сумма распределений значений, меньших, чем а.

F(a) для дискретной случайной величины является дискретной неубывающей и скачкообразной. Её можно использовать для исчисления вероятностей, а иименно:

P (x ≤ a) = F (a)

P (x > a) = 1 – F (a)

P (a< x < b) = 1 – p(x≤a) – p (x≥b) = 1 – F (a) – (1 – F(b) = F (b) – F (a).

Функция распределения для непрерывной случайной величины представляет собой непрерывную, гладкую, неубывающую прямую.

Свойства функции распределения:

1) F (- ∞) = 0

F (+ ∞) = 1

2) F (x) – неубывающая (гладкая – для непрерывных св) функция.

3) P (a < x ≤ b) = F (b) – F (b)

4) только для непрерывной величины:

P (x<a) = P (x≤a) = F (a).

Функция плотности распределения

определяется для непрерывной СВ как первая производная от функции распределения.

Тут должен быть дурацкий ненужный рисунок, но мы его опустим. Главное, что стоит взять на заметку из это рисунка, это то, что площадь области, слева от какой-либо точки на прямой x, находящаяся под графиком, почему-то численно равняя вероятности значения этой точки.

Свойства функции плотности распределения:

1.

2.

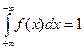
3.

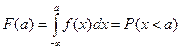
4.

Основные распределения теоретической статистики.

Распределений случайных величин существует бесконечное множество. Из них для целей статистического вывода используются несколько десятков. В социальных науках чаще всего используют четыре теоретических распределений для непрерывных случайных величин:

1. Нормальное распределение Гаусса.

2. Распределение Стьюдента.

3. Распределение Фишера.

4. «Х-квадрат – распределение».

Для всех теоретических распределений были составлены таблицы, содержащие значения F(x) для всех допустимых для данного распределения значений.

Итак, рассмотрим все распределения поподробнее.

Класс нормальных распределений (N) представляет собой симметричные колокола, форма и расположение которых описывается двумя параметрами: математическим ожиданием (µ) и средним квадратическим отклонением (σ): N(µ,σ).

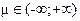определяет расположение центра распределения (наивысшей точки колокола).

σ >0, определяет форму распределения.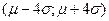

Для решения прикладных задач среди всех нормальных распределений в качестве базового выбрано распределение, где µ=0, а σ=1. Сие распределение именуется Стандартным нормальным распределением (Z) и таблицы именно этого распределения используются для решения всех задач, где встречаются нормальные распределения с любыми параметрами µ и σ.

Переход от стандартного нормального распределения (Z) нормальному распределению (N) с произвольными параметрами (µ,σ) по формуле z-оценок:

=>

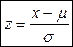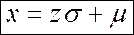
X относится к нормальному распределению с произвольными параметрами N(µ,σ), а z – к стандартному распределению Z(0;1).

При использовании формул квантили нормального распределения переходят в квантили стандартного нормального распределения и наоборот.

Рассмотрим на примерах:

У нас есть нормально распределение N с параметрами µ=-1 и σ=3.

1) P (x<1) – находим вероятность того, что x < 1

Переведем квантиль нормального распределения в квантиль стандартного нормального распределения по вышеприведенным формулам:

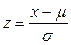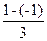= =0,67

Мы имеем в виду, что P(z<0,67)= P(x<1), потому как распределения в принципе одинаковы и отличны только формой и расположением центра колокола.

Теперь мы ищем нужное значение вероятности в таблице:

P(z<0,67) = 0,7486 = P(x<1), что и буде искомым ответом.

2) P(x>3)

Аналогичным способом тут мы находим квантиль для стандартного нормального распределения (Z), соответствующий квантилю 3 для нормального распределения (N): z = 1,33.

P(z>1,33)= P(x>3).

Откуда какие цифры взялись!?

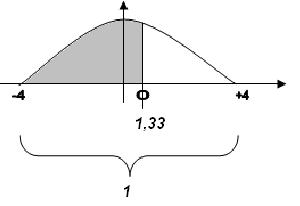
В таблице мы можем найти вероятность того, что z<1,33 (то есть площадь, затененную на рисунке). Однако мы помним, что вся площадь под колоколом равна 1 (то суммарная вероятность всех значений распределения равна единице). Теперь не трудно определить и площадь справа от квантиля (незатененный участок), равную вероятности того, что z>1,33.

Итак: P(z>1,33) = 1 – P(z<1,33) = 1 – 0,96824 = 0,03176 = P(x>3).

3) P(-3<x<3)

Начинаем с того же – находим квантили для стандартного распределения:

z_-3 = -0,67

z₃ = 1,33

P(-3<x<3) = P(-0,67<z<1,33)

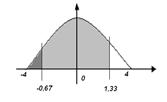
По таблице мы можем найти всю затемненную часть графика (P(z<1,33)) и затемненную ярче (P(z<-0,67)). Искомая часть затемнена светлее (интервал от -0,67 до 1,33). Не сложно догадаться, что достаточно вычесть из вероятности P(z<1,33) вероятность P(z<-0,67) чтобы получить искомое значение.

P(z<1,33) = 0,9824

P(z<-0,67) = 0,2514

P(-3<x<3) = P(-0,67<z<1,33) = P(z<1,33) - P(z<-0,67) = 0,65684.

4) P()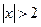

Разложив это неравенство так, чтобы избавиться от модуля, получим следующую систему неравенств:

, если изобразить это же графически

, то нам нужно найти две затемненные части.

мы можем сразу посмотреть в таблице, чтобы найти 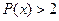, нам нужно из единицы вычесть и . Естественно, работаем мы с таблицей значений для стандартного распределения и для начала находим квантили стандартного распределения соответствующие квантилям -2 и 2 для нормального распределения.

= = P(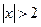) = 0,5294.

5)

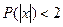
Преобразовав этот пример, получим новый: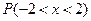

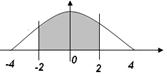
Как решаются примеры такого типа описано выше.

Дата добавления: 2014-01-11